
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Силовий розрахунок шарнірно-важільного механізмуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Розглянемо графічний метод силового дослідження плоских важільних механізмів шляхом складання рівнянь рівноваги та побудови плану сил. Наведемо розрахунок шестиланкового кулісного механізму поперечно-стругального верстата. Вихідними даними для розрахунку є: кінематична схема механізму в заданому положенні (рис. 3.8); маси mi та моменти інерції ISi ланок; положення їх центрів мас si; кутова швидкість
Рис. 3.8 Невідомими є реакції у кінематичних парах та зрівноважувальна сила Fзр. Оскільки у даному прикладі задано, що верстат з’єднаний з двигуном за допомогою зубчастої передачі Підкреслимо, що до силового розрахунку приступають лише після виконання кінематичного аналізу. Припустимо, що кінематичний розрахунок виконаний, і, отже, відомі повні прискорення центрів мас усіх ланок та їх кутові прискорення за величиною та напрямком. За знайденими прискореннями визначаємо модулі та напрями головних векторів та головних моментів сил інерції всіх ланок за формулами
Вектори сил інерції Визначимо сили ваги усіх рухомих ланок за рівністю
і прикладемо їх у центрах мас sі ланок вниз по вертикалі. Розбиваємо механізм на групи Ассура. Даний механізм утворений шляхом послідовного приєднання до механізму І класу (ланки 1,6) двох груп Ассура другого класу: групи третього виду (ланки 2,3) та другого виду (ланки 4,5).
Рис. 3.9 Накреслимо в масштабі найвіддаленішу від вхідної ланки групу Ассура (ланки 4,5) і нанесемо діючі на неї сили: корисного опору Fp, ваги G4, G5, сили (і моменти сил) інерції Ф4, Ф5, МФ4 – усі вони відомі; а також реакції від’єднаних від групи Ассура ланок (рис. 3.9, а). Невідомими є реакції. Реакція стояка на повзун R56 нормальна до напрямної UW. Невідомим є її модуль, а також точка прикладання, яка визначається через плече b. Реакцію в обертальній парі Q, невідому за модулем і напрямом, розкладемо на дві складові
Під дією цих сил, згідно з принципом Д’Аламбера, група Ассура перебуватиме в стані умовної рівноваги. Складову
звідки
де QN, h1, h2 - плечі сил, які вимірюємо на кресленні групи Ассура. Якщо права частина рівності додатна то це означає, що напрям реакції Подальші силові розрахунки проводимо графічним методом. Складаємо векторне рівняння рівноваги сил, прикладених до всієї групи Ассура (4,5):
пам’ятаючи, що для системи, яка перебуває в рівновазі, многокутник сил буде замкненим. Будуємо план сил. Для цього вибираємо масштаб
Рис. 3.10
Модулі знайдених реакцій визначаємо за відомими формулами
де Для визначення реакцій
Розв’язок отримуємо, замкнувши на плані сил точки d і f. Модуль реакції дорівнює Визначимо координату b точки прикладання реакції
отримаємо:
Якщо плече b буде мати таку довжину, що т. D виявиться поза поверхнею UW, то силова дія стояка 6 на повзун 5 зведеться до двох реакцій
Перейдемо до розгляду групи Ассура 2. Накреслимо в масштабі групу Ассура і прикладемо діючі сили (рис. 3.9, в). Двоповодкова група Ассура третього виду частіше за інші зустрічається в сучасному машинобудуванні. При цьому, часто G2 =0, Ф2 =0 або настільки малі, що ними нехтують До ланок групи прикладені: відома з попереднього розрахунку реакція Розглянемо рівновагу не групи Ассура, а окремих ланок, які входять до групи, оскільки відомо напрям реакції R32 повзуна на кулісу (реакції у внутрішній кінематичній парі В). Ця реакція нормальна до напрямної CQ і прикладена в т. В (рис. 3.9, г). За модулем реакцію R32 знайдемо з рівняння моментів сил, що діють на кулісу, відносно т. С
звідки Із умови рівноваги повзуна (рис. 3.9, д) маємо
Реакцію R36 знаходимо методом планів сил згідно з векторним рівнянням для ланки 3 Для цього з довільно вибраної точки (полюса a, рис. 3.9, е) в масштабі Переходимо до силового розрахунку механізму І класу. Накреслимо його в масштабі (рис. 3.10, а) і нанесемо діючі сили: відому силу Сила Fзр знаходиться з рівняння моментів сил відносно т. А
звідки Fзр = Відмітимо, що силу Fзр можна також отримати і коротшим шляхом, не роблячи розбивки механізму на групи Ассура, застосувавши теорему М.Є. Жуковського. Реакцію R16 стояка 6 на кривошип 1 визначимо за допомогою побудови плану сил (рис. 3.10, б) згідно з рівнянням
За модулем невідома реакція
Теорема Жуковського
Визначення зрівноважувальної сили методом М.Є.Жуковського. У випадку задач, у яких необхідно знайти зрівноважувальну силу або зрівноважувальний момент, а визначати реакції в кінематичних парах немає потреби, використовують теорему (метод) Жуковського. Прикладом таких задач є: визначення потужності та типу двигуна, моменту інерції маховика, характеристики регулятора та інші задачі динаміки. Співвідношення між силами, прикладеними до ланок механізму (включаючи і сили інерції), можна дістати, застосувавши теорему Жуковського про жорсткий важіль: якщо для механізму, що перебуває в русі, побудувати план швидкостей, а потім вектори усіх активних сил та сил інерції, які прикладені в різних точках механізму, повернути на 900 в один і той же бік та перенести в однойменні точки плану швидкостей, то сума моментів цих сил відносно полюса буде дорівнювати нулю. Замість сил можна повертати план швидкостей на 900, а сили прикладати так, як вони показані на схемі механізму. Тоді теорему Жуковського можна сформулювати таким чином: якщо до плану швидкостей, повернутого на 900, у відповідних точках прикласти всі зовнішні сили (і моменти), сили інерції (і моменти сил інерції), а також зрівноважувальну силу (момент) і розглядати план швидкостей як жорсткий важіль, закріплений у полюсі, то під дією цих сил і моментів він буде перебувати в рівновазі, а сума моментів сил відносно полюса дорівнюватиме нулю. Таким чином, рівновазі механізму відповідає рівновага повернутого плану швидкостей, який розглядається як “жорсткий важіль”, що шарнірно закріплений в полюсі плану.
Доведення теореми ґрунтується на принципі можливих переміщень. Моменти сил, що прикладені до ланок механізму найчастіше зображають у вигляді пар сил, які переносять на план швидкостей. Якщо моменти
де Застосування важеля Жуковського дозволяє визначити шукану силу за допомогою тільки одного рівняння моментів. У випадку застосування методу плану сил необхідно провести повний силовий розрахунок механізму. Відзначимо, що метод Жуковського можна застосовувати для знаходження величини будь-якої сили, якщо точка прикладання та лінія дії цієї сили задані, а також відомі лінії дії, величини та точки прикладання усіх інших сил, які діють на ланки механізму. З наведеного випливає така послідовність визначення зрівноважувальної сили за способом Жуковського: - креслять кінематичну схему механізму у заданому положенні та вибраному масштабі з прикладеними усіма зовнішніми силами. Моменти замінюють парами сил; - будують план швидкостей, повернутий на 900; - до однойменних точок повернутого плану прикладають усі зовнішні сили, сили інерції, а також зрівноважувальну силу, зберігаючи їх напрям; - складають рівняння суми моментів усіх сил відносно полюса і визначають зрівноважувальну силу. Приклад. За допомогою важеля Жуковського визначити У довільному масштабі будуємо план швидкостей. Прикладаємо у відповідних точках плану швидкостей всі сили, повернуті на 900 за рухом стрілки годинника. При цьому моменти
Складаємо рівняння моментів відносно полюса плану швидкостей
Звідки Якщо при розв’язку даного рівняння сила
Рис. 3.11
|
||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 618; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.178.93 (0.014 с.) |

 кривошипа; сила корисного опору, в розглядуваному прикладі FР - сила різання, яка прикладена до різця (ланка 5), в напрямку, протилежному руху.
кривошипа; сила корисного опору, в розглядуваному прикладі FР - сила різання, яка прикладена до різця (ланка 5), в напрямку, протилежному руху.
 , то зовнішній силовий фактор, який прикладений до зубчастого колеса
, то зовнішній силовий фактор, який прикладений до зубчастого колеса  (ланка 1), являє собою силу, модуль якої треба визначити (напрям та точка прикладання відомі).
(ланка 1), являє собою силу, модуль якої треба визначити (напрям та точка прикладання відомі).
 прикладені в центрах мас і напрямлені в протилежну сторону до напрямків векторів відповідних прискорень aSi, моменти МФі напрямлені протилежно до кутових прискорень
прикладені в центрах мас і напрямлені в протилежну сторону до напрямків векторів відповідних прискорень aSi, моменти МФі напрямлені протилежно до кутових прискорень  .
.

 ,
,  так, щоб момент нормальної складової відносно точки N дорівнював нулю. Невідомі модуль та напрям внутрішньої реакції
так, щоб момент нормальної складової відносно точки N дорівнював нулю. Невідомі модуль та напрям внутрішньої реакції  в шарнірі N визначаються пізніше, через план сил.
в шарнірі N визначаються пізніше, через план сил. знайдемо з умови рівноваги ланки 4, за рівнянням моментів
знайдемо з умови рівноваги ланки 4, за рівнянням моментів ,
, ,
, ,
, ,
, , (5)
, (5) та вираховуємо відповідні відомим силам довжини відрізків. Потім, починаючи від довільно вибраної т. а (рис. 3.9, б), відкладаємо, згідно з рівнянням (5), вектори, що зображають ці сили FР, G5, Ф5, Ф4, G4,
та вираховуємо відповідні відомим силам довжини відрізків. Потім, починаючи від довільно вибраної т. а (рис. 3.9, б), відкладаємо, згідно з рівнянням (5), вектори, що зображають ці сили FР, G5, Ф5, Ф4, G4,  (т. а), проводимо лінію, паралельну до
(т. а), проводимо лінію, паралельну до  на кресленні групи Ассура, а через кінець вектора, що зображає
на кресленні групи Ассура, а через кінець вектора, що зображає  . Напрям їх приймається таким, щоб стрілки на векторах сил були орієнтовані в напрямку обходу контура. Повну реакцію
. Напрям їх приймається таким, щоб стрілки на векторах сил були орієнтовані в напрямку обходу контура. Повну реакцію  в шарнірі Q отримуємо графічно згідно з рівнянням
в шарнірі Q отримуємо графічно згідно з рівнянням  .
.

 - відрізки на плані сил.
- відрізки на плані сил. у внутрішній кінематичній парі N розглянемо умову рівноваги сил, що діють на ланку 4,
у внутрішній кінематичній парі N розглянемо умову рівноваги сил, що діють на ланку 4,
 .
. . З рівняння моментів усіх сил, що діють на ланку 5 відносно т. N,
. З рівняння моментів усіх сил, що діють на ланку 5 відносно т. N, ,
,
 .
. ,
,  . Знайдена
. Знайдена 
 , а також відомі сили та момент G3, Ф3, МФ Невідомими є модуль та напрям реакцій R36 i R21 в шарнірах С та В, модуль реакції взаємодії
, а також відомі сили та момент G3, Ф3, МФ Невідомими є модуль та напрям реакцій R36 i R21 в шарнірах С та В, модуль реакції взаємодії  в поступальній парі 2-
в поступальній парі 2-
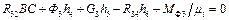 ,
, ,
,  .
. ,
, ,
,  .
. .
. відкладаємо сили
відкладаємо сили  Невідома реакція R36 замкне многокутник сил. За модулем
Невідома реакція R36 замкне многокутник сил. За модулем  .
. , силу ваги G1, невідому за модулем і напрямком реакцію R16, та невідому лише за модулем зрівноважувальну силу Fзр. В даному прикладі зрівноважувальна сила являє собою рушійну силу. Лінія дії сили Fзр проходить через полюс зачеплення Р під кутом зачеплення
, силу ваги G1, невідому за модулем і напрямком реакцію R16, та невідому лише за модулем зрівноважувальну силу Fзр. В даному прикладі зрівноважувальна сила являє собою рушійну силу. Лінія дії сили Fзр проходить через полюс зачеплення Р під кутом зачеплення  . Положення полюса Р та величина кута
. Положення полюса Р та величина кута 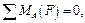
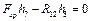 ,
, .
.
 .
.
 , що діють на ланки механізму, переносяться на план швидкостей безпосередньо у вигляді моментів, їх величина визначається рівнянням
, що діють на ланки механізму, переносяться на план швидкостей безпосередньо у вигляді моментів, їх величина визначається рівнянням
 , м – довжина ланки, до якої прикладений момент
, м – довжина ланки, до якої прикладений момент  , мм – відрізок плану швидкостей, до якого прикладається момент
, мм – відрізок плану швидкостей, до якого прикладається момент  . При цьому момент
. При цьому момент  для механізму, що зображений на рис. 3.11. Згідно з умовою,
для механізму, що зображений на рис. 3.11. Згідно з умовою,  замінюємо парою сил
замінюємо парою сил  , що прикладені в точках А та В, зі збереженням напрямку моменту
, що прикладені в точках А та В, зі збереженням напрямку моменту .
. ,
,
 .
. додатня, то це означає, що її напрям вибрано правильно. При від’ємному значенні правої частини напрям сили
додатня, то це означає, що її напрям вибрано правильно. При від’ємному значенні правої частини напрям сили 



