
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ І. Теорія механізмів і машинСодержание книги
Поиск на нашем сайте
МЕТОДИЧНІ ВКА3ІВКИ до виконання розрахунково-графічного завдання “Аналіз плоских механізмів” з курсу “Теорія механізмів і машин та деталі машин” для студентів напряму “Гірництво” денної та заочної форм навчання
М. Кривий Ріг
Укладачі: Рудь Ю.С., проф., докт. техн. наук Бурдо Ю.Й., доц., канд. техн. наук Маліновська С.І., доц., канд. техн. наук
Відповідальний за випуск: Рудь Ю.С., проф., докт. техн. наук
Рецензент: Кучма В.В., доц., канд. техн. наук
Методичні вказівки до виконання завдань з курсу “Теорія механізмів і машин та деталі машин” для студентів напряму “Гірництво” денної та заочної форм навчання є закріпленням теоретичних знань з розділу “Теорія механізмів i машин” шляхом виконання завдань зі структурного, кінематичного та кінетостатичного аналізів плоского механізму. Вказівки складаються з короткого огляду теоретичних питань та питань для самоперевірки; змісту та прикладів виконання завдань з розділу курсу “Теорія механізмів і машин та деталі машин ” “Кінематичний аналіз плоских механізмів” і “Силовий аналіз плоских механізмів”. До методичних вказівок входять 8 схем (по 10 варіантів завдань), зразок графічної частини завдань та перелік навчальної літератури.
РОЗДІЛ І. ТЕОРІЯ МЕХАНІЗМІВ І МАШИН Введення Метою завдань з кінематичного та силового аналізів плоских механізмів є закріплення теоретичних знань з розділу “Теорія механізмів i машин” шляхом виконання завдань зі структурного, кінематичного та кінетостатичного аналізів заданого плоского механізму. При виконанні першого завдання необхідно звернути увагу на такі питання: структурна класифікація механізмів за Ассуром–Артоболевським; визначення положень ланок i траєкторій точок ланок механізму; кінематичне дослідження механізму методом планів швидкостей та прискорень. Головними задачами другого завдання є визначення сил інерції ланок та реакцій у всіх кінематичних парах, зрівноважувальної сили та зрівноважувального моменту. Знання цих сил необхідно для розрахунку на міцність ланцюгів механізму та установлення їх раціональних конструкцій, призначення необхідної потужності двигуна. Пояснювальна записка виконується на аркушах паперу розміру 297´420, графічна частина – на аркушах формату А1. Пояснення, плани швидкостей, прискорень та сил, розрахунки повинні бути чіткими. З теорії механізмів та машин студенти спеціальностей ГІП, ГІВ, ОПГ, ГГ, ГБ денного відділення, ЗГІП, ЗГІВ,ЗОПГ,ЗГБ, ЗЗКК заочного відділення виконують домашнє завдання та контрольну роботу "Кінематичний аналіз плоских механізмів", а студенти спеціальності ЗКК виконують дві контрольні роботи "Кінематичний аналіз плоских механізмів" та "Кінетостатичний аналіз плоских механізмів". Студент обирає схему механізму – за останніми цифрами номера свого студентського квитка (якщо ця цифра 9 – то схема 1, 0 – схема 2), номер варіанту – за передостанньою цифрою номера студентського квитка (якщо ця цифра 0 – то варіант 10). 1. Теоретичні питання та питання для самоперевірки Структура механізмів Слід вивчити елементи, спільні для всіх механізмів, незалежно від їх цільового призначення. Важливо усвідомити різницю між ступенями вільності та числом рухів, які взагалі спостерігаються, а також різницю між абсолютними рухами ланок та відносними рухами ланок кінематичної пари, які визначаються тільки самою кінематичною парою. Для кращого засвоєння основних уявлень слід ознайомитись зі схемами більш поширених механізмів та уявити собі характер рухів їх ланок. Питання для самоперевірки 1. Наведіть визначення ланки, кінематичної пари, кінематичного ланцюга. 2. Назвіть основні плоскі кінематичні пари, поясніть розподіл пар на вищі та нижчі. 3. Які кінематичні ланцюги, замкнені чи незамкнені, використовують у механізмах? Навести визначення механізму. 4. На прикладі показати розрахунок ступеня рухомості плоского механізму. Кінематика механізмів На прикладах простих чотириланкових механізмів вивчити рішення задач кінематичного аналізу двома методами: методом кінематичних діаграм та методом планів. Під час побудови планів положень визначити крайні положення ланок та переміщення при прямому та зворотному рухах. Плани швидкостей та прискорень слід будувати на основі попередньо написаних векторних рівнянь; плани є їх графічним рішенням. Для графічного диференціювання треба згадати графічну інтерпретацію похідної та властивості функції та її похідної в характерних точках їх кривих: екстремумах, нульових значеннях, точках перегину. Динаміка механізмів Розпочавши динамічний аналіз механізмів, треба з’ясувати види сил, що діють на ланки механізмів. Перша задача динамічного аналізу полягає у визначенні сил по заданому руху ланок. Цю задачу треба розглядати на прикладі важільного чотириланкового механізму, вміти знаходити реакції в кінематичних парах, зрівноважуючий момент та зрівноважуючу силу. Послідовність знаходження реакцій у кінематичних парах базується на відділенні з механізму кінематичних ланцюгів, які статично визначені. Вирішуючи другу задачу динамічного аналізу механізмів – визначення руху ланок механізму за діючими на них силам – слід вивчити метод зведення сил та мас. Необхідно знайти рівняння руху механізму, режими руху – розбіг, сталий рух та вибіг. Слід пам'ятати, що коефіцієнт корисної дії застосовується до сталого руху. Треба знайти причини, які викликають нерівномірність сталого руху та необхідність регулювання періодичних коливань швидкості за допомогою маховика. Слід мати уяву про регулювання неперіодичних коливань швидкості регуляторами. При вивченні зрівноважування треба звертати увагу на положення загального центру мас ланки відносно осі обертання. Треба усвідомити, що зрівноважування має на меті усування (повне чи часткове) впливу на стояк динамічних навантажень від маси, що обертається на ньому (від сил інерції цієї маси). Питання для самоперевірки 1. Побудуйте плани положень кривошипно-повзунного механізму, шарнірного чотириланковика. 2. Напишіть векторні рівняння, які сполучують швидкості двох точок одної ланки та які сполучують їх прискорення. 3. Побудуйте план швидкостей та план прискорень для шарнірного чотириланковика, визначити кутові швидкості та кутові прискорення ланок за величиною та напрямом. 4. Які види сил можуть діяти на механізм при його русі? 5. Як застосувати "важіль Жуковського" для знаходження зрівноважуючої сили? 6. Що таке середня швидкість сталого руху? 7. Що таке незрівноваженість і які її наслідки особливо небезпечні? Рис. 1.3 Цей механізм є механізмом II класу. Рис. 1.5 Кутова швидкість ведучої ланки ОА ω1=20× с-1=20 рад/с Величина швидкості точки А ведучої ланки механізму: Vа= ω1·lOA=20·0,3=6 м/с Вектор швидкості точки А спрямований перпендикулярно ланці ОА в напрямку її обертання. Із точки pv – полюса плану швидкостей – проводимо вектор
Вектор Для групи 2-3 складаємо систему векторних рівнянь.
Швидкість точки А відома за значенням і напрямом. Відносна швидкість З кінця вектора VВ=рvb×μv=20×0,2=4 [м/с]. Відносна швидкість Vва=bа× μv=29× 0,2=5,8 [м/с]. Для знаходження швидкості точки Д скористаємося теоремою подібності фігур, які утворюють вектори відносних швидкостей і фігури на плані механізму. Фігура відносних швидкостей на плані швидкостей подібна фігурі на плані механізму, але повернена відносно останньої на 90° у напрямі кутової швидкості фігури механізму.
Відклавши на продовженні відрізка VДВ= рvd×mv=7×0,2=1,4 [м/с]. Швидкості центрів ваги знаходимо теж за теоремою подібності:
Кутова швидкість ланки ОА відома w1 =20 с-1, має напрям проти руху годинникової стрілки. Кутова швидкість ланки АВ визначаємо за формулою:
Для знаходження напряму руху кутової швидкості ω2 перенесемо уявно відрізок ( Кутова швидкість ланки СД:
і має напрям по годинниковій стрілці. Для визначення ω3 перенесемо уявно відрізок ( Побудова плану прискорень здійснюється в тій же послідовності, що і план швидкостей: `аА = аО+ аАО; `аО=0, то `аА =`аАО
Оскільки ланка АО рухається рівномірно (` VA = const), то ` аtAO =0. Тоді:
Вектор
Рис. 1.6 З точки ра – полюса плану прискорень – проводимо відрізок довільної довжини (
Відрізок Для групи 2-3 складаємо векторну систему рівнянь:
Прискорення точки А відоме за модулем, значенням і напрямом. Прискорення точки С дорівнює 0, тобто точка С знаходиться у полюсі. Прискорення ` аnва паралельне АB і спрямоване від точки В до точки А. Значення цього прискорення
Прискорення ` аtВA перпендикулярне АB. Модуль цього прискорення поки що невідомий. Прискорення ` аnBC паралельне ВС і спрямоване від точки В до точки С. Модуль прискорення:
Прискорення ` аtВC перпендикулярно ВС, модуль цього прискорення поки що невідомий. З кінця вектора
З точки п проводимо пряму, перпендикулярну АВ, що зображує напрям ` аtBA. З полюса ра, тобто з точки С, проводимо пряму, паралельну ВС у напрямі від точки В до точки С. На ній відкладаємо вектор
З точки m проводимо пряму, перпендикулярну ВС, яка зображує напрям ` аtВС. Точку перетину цього перпендикуляра з перпендикуляром, проведеним з точки п, позначимо точкою b. З’єднаємо точку b з полюсом і точкою а. Абсолютне прискорення точки В:
Відносне прискорення:
Для знаходження прискорень точки Д та центрів ваги, скористаємося теоремою подібності фігур, утворених векторами відносних прискорень і фігур на плані механізму: Фігура відносних прискорень на плані прискорень подібна фігурі на плані механізму, але повернена відносно неї на 180° -a у напрямі кутового прискорення фігури. Кут a визначається з рівності:
Відклавши на продовженні вектора Модуль абсолютного прискорення точки Д:
Модулі тангенціальних прискорень та прискорень центрів ваги:
Кутове прискорення ланки ОА дорівнює 0. Кутове прискорення ланки АВ:
Це прискорення спрямоване проти руху годинникової стрілки. Щоб визначити його напрям, переносимо уявно вектор ` аtBA (відрізок (mb)) у точку В механізму і розглядаємо рух цієї точки відносно точки А за напрямом прискорення ` аtBA:
Прискорення ε3 має напрям проти годинникової стрілки. Кінетостатика ведучої ланки Унаслідок силового розрахунку приєднаної до ведучої ланки групи (2-3), була знайдена реакція в кінематичній парі, якою група (2-3) приєднана до ведучої ланки.
Рис. 1.9 Розмір зрівноважуючої сили, доданої в точці А перпендикулярно ланці ОА, знаходимо з рівняння рівноваги сил і моментів, діючих на ланку ОА відносно точки О. SМ0=0
Реакцію в шарнірі О
З полюса рF (рис. 1.10) відкладаємо в масштабі:
одну за одною усі відомі сили.
Рис. 1.10 Замкнувши силовий багатокутник (з'єднавши точку О та точку РF), визначимо реакцію R41 F41=PF d×mF=62×10=620 H. 4.4. Визначення зрівноважуючої сили методом "важеля Жуковського" Якщо до плану швидкостей, повернутого на 900, у відповідних точках прикласти всі зовнішні сили і моменти, сили інерції і моменти сил інерції, а також зрівноважуючу силу, і розглядати план швидкостей як жорсткий важіль, закріплений у полюсі, то під дією цих сил і моментів він буде перебувати в рівновазі, а сума моментів сил відносно полюса дорівнюватиме нулю. Знаходимо зрівноважуючу силу методом "важеля Жуковського". Для цього будуємо (рис. 1.11), повернутий на 90° проти обертання ведучої ланки, план швидкостей. Переносимо на цей план у відповідні точки всі діючі активні сили, сили інерції та моменти сил інерції.
Рис. 1.11 ВАРІАНТИ ЗАВДАНЬ
Схема 1
Схема 2
Схема 3
Схема 4
Схема 5
Схема 6
Схема 7
Схема 8
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 312; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.242.39 (0.014 с.) |

 мм, що зображає швидкість точки А в масштабі:
мм, що зображає швидкість точки А в масштабі: .
. проводимо перпендикулярно ланці ОА в напрямку обертання.
проводимо перпендикулярно ланці ОА в напрямку обертання.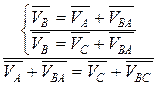 .
. відома за напрямом – вона перпендикулярна ланці АВ, але невідома за величиною. Швидкість точки С=0,
відома за напрямом – вона перпендикулярна ланці АВ, але невідома за величиною. Швидкість точки С=0, 
 , тобто вона знаходиться у полюсі pv. Відносна швидкість
, тобто вона знаходиться у полюсі pv. Відносна швидкість  перпендикулярна ланці ВС, але невідома за величиною.
перпендикулярна ланці ВС, але невідома за величиною.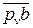 зображає на плані швидкостей абсолютну швидкість точки В; ії модуль дорівнює:
зображає на плані швидкостей абсолютну швидкість точки В; ії модуль дорівнює: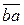 і ії модуль дорівнює:
і ії модуль дорівнює: [мм].
[мм]. (
(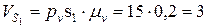 [м/с];
[м/с]; [м/с];
[м/с]; [м/с].
[м/с]. с-1.
с-1. ), що зображує
), що зображує  у точку В механізму. Він показує в якому напрямку обертається точка В і всі інші точки ланки АВ навколо точки А. Швидкість ω2 має напрям проти руху годинникової стрілки.
у точку В механізму. Він показує в якому напрямку обертається точка В і всі інші точки ланки АВ навколо точки А. Швидкість ω2 має напрям проти руху годинникової стрілки. с-1
с-1 ), що зображає
), що зображає  , у точку В механізму. Він показує, у якому напрямку обертається точка В і всі інші точки ланки ВС навколо точки С.
, у точку В механізму. Він показує, у якому напрямку обертається точка В і всі інші точки ланки ВС навколо точки С. .
. [м/с2].
[м/с2]. має напрям уздовж ланки ОА від точки А до точки О, тобто до центру обертання (рис. 1.6).
має напрям уздовж ланки ОА від точки А до точки О, тобто до центру обертання (рис. 1.6).
 мм), що зображає вектор прискорення ` аА в масштабі:
мм), що зображає вектор прискорення ` аА в масштабі: .
. проводимо паралельно ОА у напрямі від точки А до точки О.
проводимо паралельно ОА у напрямі від точки А до точки О. .
. [м/с2].
[м/с2]. [м/с2].
[м/с2]. проводимо пряму, паралельну АB, у напрямі від точки В до точки А. На ній відкладаємо вектор
проводимо пряму, паралельну АB, у напрямі від точки В до точки А. На ній відкладаємо вектор  , що зображує прискорення `аnBA. Величина цього вектора:
, що зображує прискорення `аnBA. Величина цього вектора: [мм].
[мм]. , що зображує прискорення `аnBС . Величина вектора:
, що зображує прискорення `аnBС . Величина вектора: [мм].
[мм]. [м/с2].
[м/с2]. [м/с2].
[м/с2].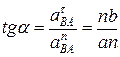 .
.
 відрізок bd =8,8 мм, одержуємо точку d.
відрізок bd =8,8 мм, одержуємо точку d. [м/с2].
[м/с2]. [м/с2];
[м/с2];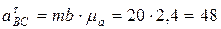 [м/с2];
[м/с2];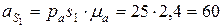 [м/с2];
[м/с2]; [м/с2];
[м/с2]; [м/с2].
[м/с2]. [с-2].
[с-2]. [с-2].
[с-2]. Креслимо ведучу ланку в масштабі ml (рис.1.9) та додаємо реакцію
Креслимо ведучу ланку в масштабі ml (рис.1.9) та додаємо реакцію  .
. ;
; Н.
Н. знайдемо побудовою замкненого багатокутника сил, що відповідає векторному рівнянню рівноваги.
знайдемо побудовою замкненого багатокутника сил, що відповідає векторному рівнянню рівноваги. .
. Н/мм
Н/мм













