
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Структурний аналіз механізмівСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Механізм – це сукупність тіл (ланок), сполучених між собою так, що заданому руху одного чи кількох з них відповідає цілком визначений рух кожного з решти. Ланки механізму, одержуючи рух від незалежних джерел (наприклад, двигунів), прийнято вважати ведучими, а останні – веденими. Ступінь рухомості механізму повинен дорівнювати числу ведучих ланок. Структурна формула П.Л. Чебишева для ступеня рухомості плоского механізму: W = 3n-2р5-р4, де n – число рухомих ланок кінематичного ланцюга, p5 – число кінематичних пар п'ятого класу; р4 – число кінематичних пар четвертого класу. Методи кінематичного аналізу механізмів пов'язані з їх структурною класифікацією. Структурна класифікація Ассура–Артоболевського є одною з найбільш раціональних класифікацій плоских механізмів. Кожен плоский механізм розглядається як складна система, що складається зі стояка, ведучих та ведених ланок. За класифікацією Ассура – Артоболевського ведуча ланка та стояк утворюють початковий механізм 1 класу (рис.1.1). Кінематичною парою називається рухоме з’єднання двох стичних ланок. Структурна група Ассура – це кінематичний ланцюг, при приєднанні якого до механізму не змінюється ступінь рухомості механізму.
Рис.1.1
У даних завданнях будемо розглядати тільки групи Ассура II класу II порядку (табл.1.1). Таблиця 1.1
де О – обертальна пара; П – поступальна пара.
1. Визначаємо число рухомих ланок: n=3 2. Визначаємо число кінематичних пар 5 класу р5=4 3. Визначаємо ступінь рухомості механізму: W=3n-2 р5-р4=3-3-2-4=1
Отже, механізм має одну ведучу ланку. Рис.1.2 Даний механізм утворений приєднанням до початкового механізму 1-4 двоповодкової групи 2-3 (рис. 1.3).
Рис. 1.3 Цей механізм є механізмом II класу. Кінематичний аналіз плоских механізмів Кінематичне дослідження плоских механізмів включає такі основні задачі: 1. Визначення положень ланок, траєкторій точок механізму. 2. Визначення величини та напряму лінійних швидкостей та прискорень точок, кутових швидкостей та прискорень ланок механізму. 3.1. Побудова плану положень ланок Побудова плану положень механізму виконується графічно методом засічок. Нехай треба визначити положення ланок та траєкторії точок механізму, кінематична схема якого зображена на рис. 1.2. Розміри ланок та закон руху ведучої ланки ОА задано. lOA=0,3 м; lAB=0,8; lBC=0,65м; lBD=0,23м; lOE=y=1,1 м lEC=х=0,09 м; j1=0°; j2=90°; w1=20 c-1 Центри ваги ланок знаходяться на серединах ланок.
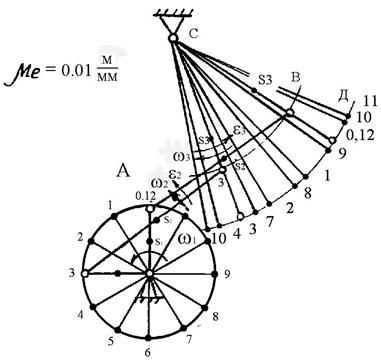
Так як ланка ОА обертається з постійною кутовою швидкістю навколо точки О, то траєкторією точки А є коло радіусом ОА (рис. 1.4). Із точки О проводимо коло радіусом 30 мм, тоді масштабний коефіцієнт довжини: ml = lОА/ОА=0,3 м /30 мм =0,01 м/мм Поділимо коло на 12 однакових частин. Позначимо положення кривошипа ОА в напрямі обертання його А1, А2, А3 і т.д. По заданим розмірам ланок у масштабі ml знаходимо положення нерухомих точок механізму О і С. З точки С проводимо дугу радіусом СВ. СВ= lCВ/ μl= 0,65 м/0,01 м/мм=65 мм.
Рис.1.4. Послідовно, із кожної точки А (А1, А2, A3 і т.д.) дугою АВ робимо на цій дузі засічки. Так знаходимо 12 положень точки В. АВ=lав/μl =0,8 м/0,01 м/мм =80 мм. Послідовно з'єднуємо точки А і В, В і С. Одержуємо 12 положень механізму. З точки С проводимо дугу СД і одержуємо траєкторію руху точки Д. СД = (lCB+lBD)/μl= (0,65 м+0,23 м)/0,01 м/мм = 88 мм. Центри ваги ланок знаходяться на серединах ланок. 3.2. Кінематичне дослідження механізмів за допомогою планів швидкостей та прискорень Метод планів має ряд переваг: простота, наочність, можливість визначення лінійних швидкостей та прискорень точок, кутових швидкостей і прискорень ланок механізму в даному його положенні. Побудова планів швидкостей і прискорень починається з ведучої ланки, закон руху якої задано. Потім послідовно розглядають групи Ассура в порядку їх з'єднання з початковим механізмом. Будуємо план швидкостей для положення механізму φ2=90° (рис. 1.5).
Рис. 1.5 Кутова швидкість ведучої ланки ОА ω1=20× с-1=20 рад/с Величина швидкості точки А ведучої ланки механізму: Vа= ω1·lOA=20·0,3=6 м/с Вектор швидкості точки А спрямований перпендикулярно ланці ОА в напрямку її обертання. Із точки pv – полюса плану швидкостей – проводимо вектор
Вектор Для групи 2-3 складаємо систему векторних рівнянь.
Швидкість точки А відома за значенням і напрямом. Відносна швидкість З кінця вектора VВ=рvb×μv=20×0,2=4 [м/с]. Відносна швидкість Vва=bа× μv=29× 0,2=5,8 [м/с]. Для знаходження швидкості точки Д скористаємося теоремою подібності фігур, які утворюють вектори відносних швидкостей і фігури на плані механізму. Фігура відносних швидкостей на плані швидкостей подібна фігурі на плані механізму, але повернена відносно останньої на 90° у напрямі кутової швидкості фігури механізму.
Відклавши на продовженні відрізка VДВ= рvd×mv=7×0,2=1,4 [м/с]. Швидкості центрів ваги знаходимо теж за теоремою подібності:
Кутова швидкість ланки ОА відома w1 =20 с-1, має напрям проти руху годинникової стрілки. Кутова швидкість ланки АВ визначаємо за формулою:
Для знаходження напряму руху кутової швидкості ω2 перенесемо уявно відрізок ( Кутова швидкість ланки СД:
і має напрям по годинниковій стрілці. Для визначення ω3 перенесемо уявно відрізок ( Побудова плану прискорень здійснюється в тій же послідовності, що і план швидкостей: `аА = аО+ аАО; `аО=0, то `аА =`аАО
Оскільки ланка АО рухається рівномірно (` VA = const), то ` аtAO =0. Тоді:
Вектор
Рис. 1.6 З точки ра – полюса плану прискорень – проводимо відрізок довільної довжини (
Відрізок Для групи 2-3 складаємо векторну систему рівнянь:
Прискорення точки А відоме за модулем, значенням і напрямом. Прискорення точки С дорівнює 0, тобто точка С знаходиться у полюсі. Прискорення ` аnва паралельне АB і спрямоване від точки В до точки А. Значення цього прискорення
Прискорення ` аtВA перпендикулярне АB. Модуль цього прискорення поки що невідомий. Прискорення ` аnBC паралельне ВС і спрямоване від точки В до точки С. Модуль прискорення:
Прискорення ` аtВC перпендикулярно ВС, модуль цього прискорення поки що невідомий. З кінця вектора
З точки п проводимо пряму, перпендикулярну АВ, що зображує напрям ` аtBA. З полюса ра, тобто з точки С, проводимо пряму, паралельну ВС у напрямі від точки В до точки С. На ній відкладаємо вектор
З точки m проводимо пряму, перпендикулярну ВС, яка зображує напрям ` аtВС. Точку перетину цього перпендикуляра з перпендикуляром, проведеним з точки п, позначимо точкою b. З’єднаємо точку b з полюсом і точкою а. Абсолютне прискорення точки В:
Відносне прискорення:
Для знаходження прискорень точки Д та центрів ваги, скористаємося теоремою подібності фігур, утворених векторами відносних прискорень і фігур на плані механізму: Фігура відносних прискорень на плані прискорень подібна фігурі на плані механізму, але повернена відносно неї на 180° -a у напрямі кутового прискорення фігури. Кут a визначається з рівності:
Відклавши на продовженні вектора Модуль абсолютного прискорення точки Д:
Модулі тангенціальних прискорень та прискорень центрів ваги:
Кутове прискорення ланки ОА дорівнює 0. Кутове прискорення ланки АВ:
Це прискорення спрямоване проти руху годинникової стрілки. Щоб визначити його напрям, переносимо уявно вектор ` аtBA (відрізок (mb)) у точку В механізму і розглядаємо рух цієї точки відносно точки А за напрямом прискорення ` аtBA:
Прискорення ε3 має напрям проти годинникової стрілки.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 626; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.01 с.) |



 Приклад. Визначити ступінь рухомості та виконати структурний аналіз механізму щокової дробарки (рис. 1.2).
Приклад. Визначити ступінь рухомості та виконати структурний аналіз механізму щокової дробарки (рис. 1.2).

 мм, що зображає швидкість точки А в масштабі:
мм, що зображає швидкість точки А в масштабі: .
. проводимо перпендикулярно ланці ОА в напрямку обертання.
проводимо перпендикулярно ланці ОА в напрямку обертання.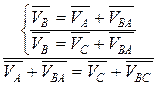 .
. відома за напрямом – вона перпендикулярна ланці АВ, але невідома за величиною. Швидкість точки С=0,
відома за напрямом – вона перпендикулярна ланці АВ, але невідома за величиною. Швидкість точки С=0, 
 , тобто вона знаходиться у полюсі pv. Відносна швидкість
, тобто вона знаходиться у полюсі pv. Відносна швидкість  перпендикулярна ланці ВС, але невідома за величиною.
перпендикулярна ланці ВС, але невідома за величиною.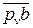 зображає на плані швидкостей абсолютну швидкість точки В; ії модуль дорівнює:
зображає на плані швидкостей абсолютну швидкість точки В; ії модуль дорівнює: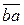 і ії модуль дорівнює:
і ії модуль дорівнює: [мм].
[мм]. (
(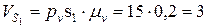 [м/с];
[м/с]; [м/с];
[м/с]; [м/с].
[м/с]. с-1.
с-1. ), що зображує
), що зображує  у точку В механізму. Він показує в якому напрямку обертається точка В і всі інші точки ланки АВ навколо точки А. Швидкість ω2 має напрям проти руху годинникової стрілки.
у точку В механізму. Він показує в якому напрямку обертається точка В і всі інші точки ланки АВ навколо точки А. Швидкість ω2 має напрям проти руху годинникової стрілки. с-1
с-1 ), що зображає
), що зображає  , у точку В механізму. Він показує, у якому напрямку обертається точка В і всі інші точки ланки ВС навколо точки С.
, у точку В механізму. Він показує, у якому напрямку обертається точка В і всі інші точки ланки ВС навколо точки С. .
. [м/с2].
[м/с2]. має напрям уздовж ланки ОА від точки А до точки О, тобто до центру обертання (рис. 1.6).
має напрям уздовж ланки ОА від точки А до точки О, тобто до центру обертання (рис. 1.6).
 мм), що зображає вектор прискорення ` аА в масштабі:
мм), що зображає вектор прискорення ` аА в масштабі: .
. проводимо паралельно ОА у напрямі від точки А до точки О.
проводимо паралельно ОА у напрямі від точки А до точки О. .
. [м/с2].
[м/с2]. [м/с2].
[м/с2]. проводимо пряму, паралельну АB, у напрямі від точки В до точки А. На ній відкладаємо вектор
проводимо пряму, паралельну АB, у напрямі від точки В до точки А. На ній відкладаємо вектор  , що зображує прискорення `аnBA. Величина цього вектора:
, що зображує прискорення `аnBA. Величина цього вектора: [мм].
[мм]. , що зображує прискорення `аnBС . Величина вектора:
, що зображує прискорення `аnBС . Величина вектора: [мм].
[мм]. [м/с2].
[м/с2]. [м/с2].
[м/с2].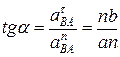 .
.
 відрізок bd =8,8 мм, одержуємо точку d.
відрізок bd =8,8 мм, одержуємо точку d. [м/с2].
[м/с2]. [м/с2];
[м/с2];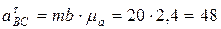 [м/с2];
[м/с2];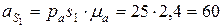 [м/с2];
[м/с2]; [м/с2];
[м/с2]; [м/с2].
[м/с2]. [с-2].
[с-2]. [с-2].
[с-2].


