
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зрівноважування механізмів на фундаментіСодержание книги
Поиск на нашем сайте
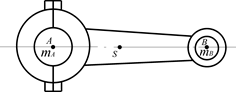
Розглянемо причини незрівноважності механізмів на прикладі шарнірного чотириланковика, початкова ланка якого обертається зі сталою кутовою швидкістю
Сила Якщо
Рис. 6.1. Під час проектування механізмів для статичного зрівноважування, застосовують низку заходів з метою досягнення умови З теоретичної механіки відомо, що сила інерції
а б Рис. 6.2. Розглянемо цей метод. Відомо, що будь-яке тіло масою
Виконання тільки умов (1) і (2) називається статичним розміщенням мас і воно зводиться до того, що головний вектор сил інерції замінюючої системи мас дорівнює головному вектору сил інерції заданого тіла. Однак, при цьому головний момент сил інерції системи мас не дорівнює головному моменту сил інерції тіла. Але для статичного зрівноважування таке розміщення мас припустиме. Виконаємо статичне заміщення маси
Рис. 6.3. Розглянемо методику статичного зрівноваження механізму шарнірного чотириланковика (рис. 6.3, а). Замінимо масу кожної ланки
Об’єднаємо маси, розміщенні в точках B і C:
Отже, маси усіх ланок механізму виявляються заміненими чотирма масами, зосередженими в точках A, B, C, D. При цьому центр мас
Об’єднавши маси розташовані на ланках 1 і 3 (рис. 6.3, б), дістанемо
Таким чином, після розміщення противаг заданий механізм замінюєтося системою двох нерухомих мас: 6.2. Зрівноваження обертових ланок (роторів)
Ротором у теорії балансування (зрівноваження) називають будь-яке тіло, що обертається. У сучасних машинах та механізмах використовується величезна кількість роторів. Це, наприклад, ротори електродвигунів, генераторів, турбін, центрифуг, помп, вентиляторів, автомобільні колеса, колінчасті та кулачкові вали, шпинделі верстатів, абразивні та шліфувальні круги, ротори приводів CD і DVD дисків, тощо. З курсу теоретичної механіки відомо, що тиск тіла, що обертається на свої опори в загальному випадку, складається з двох складових: статичної, яка викликана дією заданих сил (силою ваги і т.п.) та динамічної, що зумовлена прискореним рухом елементарних мас, з яких складається обертове тіло. Якщо динамічна складова не дорівнює нулю, то ротор вважається незрівноваженим. Необхідність зрівноваження роторів, що обертаються з високими швидкостями можна пояснити наступним прикладом: незрівноважений ротор масою – у випадку швидкості ротора, а при Отже, під час обертання ланок з великою кутовою швидкістю навіть порівняно невеликі незрівноважені маси цих ланок можуть спричинити виникнення значних сил інерції і відповідних динамічних реакцій на опори (підшипники). Крім того, необхідно особливо відмітити, що на відміну від сил ваги, сили інерції, а отже, і динамічні реакції є змінними за напрямком і можуть викликати коливання та вібрацію ланок. Відмітимо, що за умови Будь-яке тверде тіло складається з нескінченно великого числа елементарних мас. Нехай деяка елементарна маса
У векторному вигляді можна записати
де Модуль головного вектора відцентрових сил інерції визначається за формулою При рівномірному обертанні ротора проекції динамічної складової тиску ротора на опори визначається таким чином
Незрівноваженість ротора чисельно оцінюють за допомогою головного вектора та головного моменту відцентрових сил інерції ротора. Ротор вважається зрівноваженим, якщо головний вектор та головний момент сил інерції дорівнює нулю і, отже, ротор не чинить ніяких динамічних тисків на опори
Якщо ж Усунення динамічних навантажень на опори називається балансуванням (зрівноваженням). Розв’язок даної задачі відноситься до динамічного проектування машин.
Рис. 6.4
Позначимо Зазначимо, що на практиці незрівноваженість ротора характеризують не через Види незрівноваженості ротора. На рис. 6.5 наведені різні випадки незрівноваженості ротора. Статична незрівноваженість. При статичній незрівноваженості головна центральна вісь ротора
Рис. 6.5
Статичне балансування проводять лише для роторів, що обертаються з малими швидкостями та мають невеликі розміри у напрямку осі обертання. Тобто, для роторів з невеликою шириною порівняно з діаметром роторів, які можна розглядати як систему точкових мас, розміщених в одній площині. У цьому випадку одночасно зі статичним зрівноваженням виконується умова повного зрівноваження. Умовою статичної зрівноваженості ротора є рівність нулю головного вектора відцентрових сил інерції; тобто дисбаланс ротора має дорівнювати нулю, і, отже, центр мас ротора – бути на осі обертання. Виконаємо статичне зрівноваження ротора, що має деякий дисбаланс. Сила інерції незрівноваженої маси ротора в загальному випадку визначається за формулою
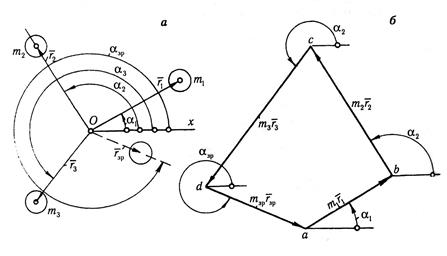
Звідси умова підбору противаг Центр мас противаги повинен бути на лінії дії вектора З (4) випливає, що ротор зрівноважений при деякому значенні Зрівноваження декілька мас, що обертаються в одній площині. Необхідно зрівноважити три маси, які знаходяться на валу в одній площині (рис. 6.6), тобто знайти величину і положення зрівноваженої маси, якщо задані
Рис. 6.6 Обчислюємо величину статичних дисбалансів мас (добуток маси на відстань її від осі обертання):
Складаємо рівняння рівноваги обертових мас у вигляді суми усіх статичних дисбалансів, яка у випадку рівноваги повинна дорівнювати нулю
Будуємо, згідно з цим рівнянням замкнений векторний контур статичних дисбалансів (рис. 6.6). Побудову здійснюємо у масштабі
Векторам дисбалансів З’єднавши кінець вектора
Моментна незрівновженість. Має місце, коли центр мас
Прикладом може бути неточний монтаж шківа на валу. Динамічна незрівноваженість. В разі динамічної незрівноваженості ротора його головна центральна вісь
Балансування твердого ротора – це процес суміщення головної центральної осі ротора з його віссю обертання.
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 569; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.90.108 (0.01 с.) |

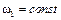 . При цьому на ланки будуть діяти сили й моменти сил інерції (рис. 6.1, а). Зведемо всю систему сил інерції до точки А (рис. 6.1, б). В результаті вона зведеться до головного вектора
. При цьому на ланки будуть діяти сили й моменти сил інерції (рис. 6.1, а). Зведемо всю систему сил інерції до точки А (рис. 6.1, б). В результаті вона зведеться до головного вектора  і головного моменту
і головного моменту
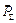 і момент
і момент 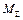 передаються на основу О і викликають реакції в місцях кріплення K і N.
передаються на основу О і викликають реакції в місцях кріплення K і N.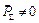 , то механізм є статично незрівноваженим; якщо
, то механізм є статично незрівноваженим; якщо 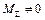 , то механізм динамічно незрівноважений; якщо
, то механізм динамічно незрівноважений; якщо 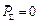 , але
, але 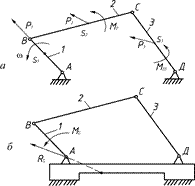
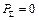 . При цьому не ставиться задача одночасного виконання умови
. При цьому не ставиться задача одночасного виконання умови  . Тобто статично зрівноважений механізм ніякої динамічної дії на основу у вигляді сили не чинить. Водночас такий механізм, в загальному випадку, може чинити динамічний вплив на фундамент у вигляді моменту.
. Тобто статично зрівноважений механізм ніякої динамічної дії на основу у вигляді сили не чинить. Водночас такий механізм, в загальному випадку, може чинити динамічний вплив на фундамент у вигляді моменту.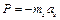 , де
, де 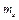 – маса системи рухомих ланок;
– маса системи рухомих ланок;  – прискорення центра S мас цієї системи. Умова
– прискорення центра S мас цієї системи. Умова 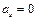 , тобто коли центр мас не переміщується. Таким чином, статичне зрівноважування – це така дія, у результаті якої центр мас стає нерухомим. Для досягнення статичного зрівноваження механізму використовують метод замінювальних мас.
, тобто коли центр мас не переміщується. Таким чином, статичне зрівноважування – це така дія, у результаті якої центр мас стає нерухомим. Для досягнення статичного зрівноваження механізму використовують метод замінювальних мас.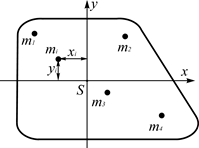
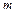 можна замінити системою
можна замінити системою 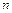 зосереджених мас (рис. 6.2, а), поставивши вимоги – щоб сума усіх мас системи дорівнювала масі тіла, центр мас залишився на тому ж місці з попереднім моментом інерції:
зосереджених мас (рис. 6.2, а), поставивши вимоги – щоб сума усіх мас системи дорівнювала масі тіла, центр мас залишився на тому ж місці з попереднім моментом інерції: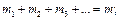 (1)
(1)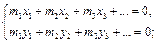 (2)
(2)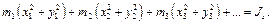 (3)
(3) двома масами зосередженими в шарнірах
двома масами зосередженими в шарнірах 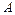 та
та 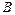 (рис. 6.2, б):
(рис. 6.2, б): 
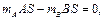 звідки
звідки
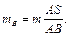
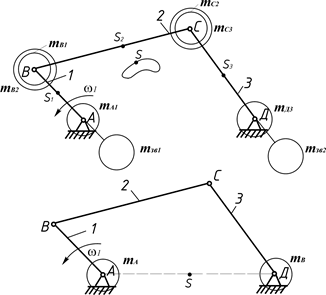
 двома масами, зосередженими в шарнірах:
двома масами, зосередженими в шарнірах: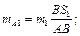
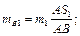
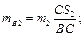
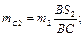


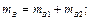

 системи залишається у тому самому місці й рухається з прискоренням
системи залишається у тому самому місці й рухається з прискоренням 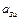 , тобто це статистично незрівноважена система ланок. Розмістимо на ланках 1 і 3 противаги з таким розрахунком, щоб центри мас
, тобто це статистично незрівноважена система ланок. Розмістимо на ланках 1 і 3 противаги з таким розрахунком, щоб центри мас  і
і 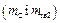 перемістилися б у нерухомі точки A і D. Для цього виконуємо співвідношення
перемістилися б у нерухомі точки A і D. Для цього виконуємо співвідношення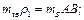

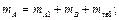
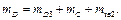
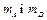 . Центр мас
. Центр мас 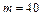 кг, обертається зі швидкістю,
кг, обертається зі швидкістю, 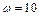 с-1 (
с-1 (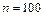 об/хв), ексцентриситет ротора
об/хв), ексцентриситет ротора  мм, у цьому випадку виникає відцентрова сила інерції
мм, у цьому випадку виникає відцентрова сила інерції 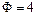 Н;
Н;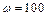 с-1 (
с-1 ( об/хв) –
об/хв) –  Н;
Н;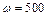 с-1 (
с-1 (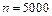 об/хв) –
об/хв) –  Н. Що в 25 разів більше за навантаження від тиску на опори сили ваги самої деталі (
Н. Що в 25 разів більше за навантаження від тиску на опори сили ваги самої деталі ( Н). Відповідно, у випадку незрівноваженості ротора, істотно зростуть реакції в його опорах. У той же час є ротори з частотою обертання 75; 100 тис. об/хв.
Н). Відповідно, у випадку незрівноваженості ротора, істотно зростуть реакції в його опорах. У той же час є ротори з частотою обертання 75; 100 тис. об/хв.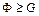 при кожному оберті ротора буде відбуватися його “підкидання” вгору, тобто ротор буде „бити”. Подаючи дану умову у вигляді,
при кожному оберті ротора буде відбуватися його “підкидання” вгору, тобто ротор буде „бити”. Подаючи дану умову у вигляді,  мм можна констатувати, що ротор, який обертається з кутовою швидкістю
мм можна констатувати, що ротор, який обертається з кутовою швидкістю 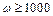 с-1 незалежно від його маси починає „бити” вже в разі
с-1 незалежно від його маси починає „бити” вже в разі 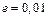 мм.
мм. , розміщена на відстані
, розміщена на відстані 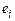 від осі обертання
від осі обертання 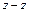 і на відстані
і на відстані 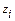 від площини
від площини 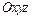 , яка проходить через центр мас ротора перпендикулярно до його осі обертання (рис. 6.4). Усі відцентрові сили інерції елементарних мас, що виникають при обертанні ротора можна привести до головного вектора
, яка проходить через центр мас ротора перпендикулярно до його осі обертання (рис. 6.4). Усі відцентрові сили інерції елементарних мас, що виникають при обертанні ротора можна привести до головного вектора 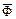 і головного моменту
і головного моменту 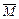 сил інерції
сил інерції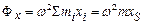 ,
, 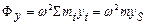 .
.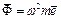 ;
; ,
,  ,
,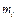 – елементарна маса;
– елементарна маса; 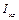 ,
, 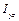 – відцентрові моменти інерції ротора відносно системи координат
– відцентрові моменти інерції ротора відносно системи координат  – радіус-вектор центра мас
– радіус-вектор центра мас  ротора, або ексцентриситет ротора.
ротора, або ексцентриситет ротора. . Модуль головного моменту відцентрових сил інерцій можна подати у вигляді
. Модуль головного моменту відцентрових сил інерцій можна подати у вигляді  .
.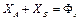 ,
,  ,
,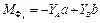 ,
, 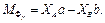
 .
. – ротор є незрівноваженим.
– ротор є незрівноваженим.
 – вектор, що називається головним вектором дисбалансів ротора, або
– вектор, що називається головним вектором дисбалансів ротора, або 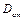 це статичний дисбаланс ротора, вимірюється у
це статичний дисбаланс ротора, вимірюється у  . Звичайно
. Звичайно  . Аналогічно
. Аналогічно  – це моментний дисбаланс ротора (динамічний дисбаланс), вимірюється
– це моментний дисбаланс ротора (динамічний дисбаланс), вимірюється 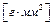 . Звичайно
. Звичайно 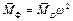 .
.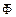 та
та 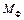 , а через пропорційні їм головний вектор
, а через пропорційні їм головний вектор 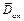 і головний момент
і головний момент  дисбалансів ротора.
дисбалансів ротора.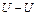 паралельна осі обертання
паралельна осі обертання 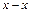 (головна вісь інерції – вісь
(головна вісь інерції – вісь  та
та 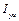 дорівнюють нулю). При цьому центр мас ротора знаходиться на відстані
дорівнюють нулю). При цьому центр мас ротора знаходиться на відстані 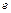 від цієї осі. Відцентрові сили зводяться до рівнодіючої, прикладеної до центра мас ротора. Тобто, у цьому випадку
від цієї осі. Відцентрові сили зводяться до рівнодіючої, прикладеної до центра мас ротора. Тобто, у цьому випадку 
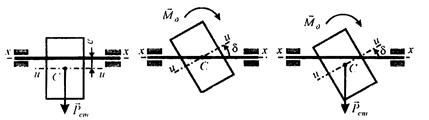
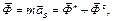 де
де  . Тоді
. Тоді  З теоретичної механіки відомо, що силу можна зрівноважити лише силою, рівною їй за модулем, яка діє вздовж тієї ж прямої і спрямована у протилежний бік. Таку силу можна створити за допомогою встановлення додаткової маси противаги, тобто
З теоретичної механіки відомо, що силу можна зрівноважити лише силою, рівною їй за модулем, яка діє вздовж тієї ж прямої і спрямована у протилежний бік. Таку силу можна створити за допомогою встановлення додаткової маси противаги, тобто
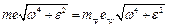 . (4)
. (4)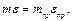 тобто
тобто 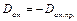
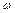 , зберігає свою зрівноваженість для будь-якої кутової швидкості, як постійної так і змінної.
, зберігає свою зрівноваженість для будь-якої кутової швидкості, як постійної так і змінної.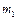 ,
, 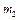 ,
, 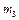 ,
, 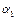 ,
, 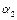 ,
, 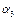 ,
, 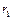 ,
, 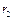 ,
, 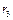 .
.
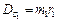 ;
; 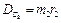 ;
; 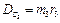 .
.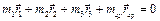 або
або 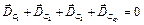 .
.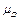 . Тоді відрізки, які відображають відповідні вектори, будуть:
. Тоді відрізки, які відображають відповідні вектори, будуть: .
.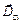 надаємо такі напрямки, які мають радіус-вектори
надаємо такі напрямки, які мають радіус-вектори  ; кути
; кути  вимірюємо від лінії, що проходить через початок відповідного вектора паралельно осі обертання
вимірюємо від лінії, що проходить через початок відповідного вектора паралельно осі обертання 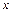 .
.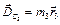 (точку
(точку 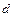 ) з початком вектора
) з початком вектора 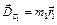 (точкою
(точкою  ), знаходимо величину
), знаходимо величину  і напрямок
і напрямок  зрівноважувального вектора
зрівноважувального вектора 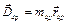 . Задавшись, наприклад величиною радіуса, знаходимо зрівноважуючу масу
. Задавшись, наприклад величиною радіуса, знаходимо зрівноважуючу масу 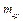
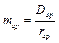 .
.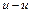 перетинається з віссю обертання
перетинається з віссю обертання 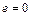 ,
, 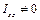 ,
,  ; відцентрові сили інерції зводяться до однієї пари сил з моментом, що дорівнює головному моменту. Оскільки пара сил зрівноважується тільки парою, то усунути моментну незрівноваженість можна лише як мінімум двома противагами.
; відцентрові сили інерції зводяться до однієї пари сил з моментом, що дорівнює головному моменту. Оскільки пара сил зрівноважується тільки парою, то усунути моментну незрівноваженість можна лише як мінімум двома противагами.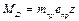 .
.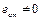 ,
, 


