
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез чотириланкових механізмів за двома положеннями ланокСодержание книги
Поиск на нашем сайте
Задачі синтезу важільних механізмів за положеннями ланок можуть бути розв’язані аналітично, наприклад, методом інтерполяції. Частіше, проте, використовуються графічні побудови. Шарнірний чотириланковик. Задано відстань
Рис. 7.2
З’єднаємо прямими лініями точки С1 та С2 з точкою А. Тоді
звідки При розв’язку цієї задачі положення т. А – осі обертання кривошипа, вибираємо довільним, отже, в загальному випадку задача має багато розв’язків. При проектуванні механізмів потрібно враховувати такий досить важливий параметр, як кут тиску. Кут тиску У шарнірному чотириланковику кут тиску досягає максимального значення, якщо положення кривошипа АВ співпадає з лінією центрів АD, тобто Розглянемо ще одну задачу проектування шарнірного чотириланковика за двома положеннями ланок. Вона менш характерна, але є досить наочною. Нехай, необхідно знайти розміри ланок шарнірного чотириланковика АВСD, у якому шатун ВС з’єднаний зі столом Т; при цьому стіл повинен мати можливість приймати два положення, які повернуті одне відносно іншого на 1800 (рис. 7.2, б). Таким чином, задано два положення стола Т, і відповідно - шатуна: В1С1 та В2С2 (положення шарнірів В та С на столі Т вибираються довільно). Очевидно, що точки В1, В2 повинні лежати на колі з центром у шуканій точці А обертання кривошипа. Цей центр лежить на прямій аа, яка проведена перпендикулярно до відрізка В1В2 через його середину. Аналогічно шуканий центр D обертання коромисла лежить на прямій dd, що проведена перпендикулярно до прямої С1С2 через її середину. Вибираючи положення центрів обертання А та Dу довільних точках прямих аа та dd, отримуємо різні варіанти механізму. Для одержання однозначного розв’язку необхідно врахувати якусь додаткову умову.
Кривошипно-повзунний механізм (рис. 7.3, а). Нехай задано хід повзуна h, або два його крайні положення – точки С0, С/0. Для центрального кривошипно-повзунного механізму хід повзуна дорівнює подвоєній довжині кривошипа;
Рис. 7.3
У розглядуваному випадку необхідно також врахувати допустимий кут тиску. Якщо веденою ланкою є повзун, то максимальний кут тиску Зауважимо, що при веденому кривошипі кут тиску У кривошипно-повзунному механізмі зі зміщенням e хід повзуна h вже не дорівнює
Звідси при заданих Кулісний механізм. Розглянемо конструктивний різновид механізму, що застосовується в гідроприводах (рис. 7.3, б). Особливість його у тому, що ведуча ланка – поршень 2 не з’єднується зі стояком. При переході з одного крайнього положення в інше поршень, що рухається під тиском рідини, переміщується на відстань h (хід поршня). При цьому ведене коромисло 1 довжиною
З
Проектування з урахуванням кута тиску. Задано кутове переміщення веденої ланки Відкладемо кут розмаху коромисла
|
||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.210.41 (0.009 с.) |

 між нерухомими точками механізму, довжину веденого коромисла
між нерухомими точками механізму, довжину веденого коромисла 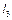 та два його крайніх положення, за допомогою кутів
та два його крайніх положення, за допомогою кутів 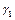 і
і  (рис. 7.2, а). Необхідно знайти довжину кривошипа
(рис. 7.2, а). Необхідно знайти довжину кривошипа 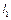 та шатуна
та шатуна 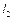 .
.
 ,
, . (7.5)
. (7.5) - кут між вектором сили, яка прикладена до ланки, та вектором швидкості точки прикладання сили (тертя при цьому не враховується). Як відомо, кут тиску характеризує ефективність передачі сил та працездатність механізму; кут тиску не повинен перевищувати допустимого значення,
- кут між вектором сили, яка прикладена до ланки, та вектором швидкості точки прикладання сили (тертя при цьому не враховується). Як відомо, кут тиску характеризує ефективність передачі сил та працездатність механізму; кут тиску не повинен перевищувати допустимого значення,  . Таким чином, при синтезі необхідно перевіряти величину кута тиску у тих положеннях механізму, в яких кут досягає максимальних значень (часто обмежуються робочим ходом).
. Таким чином, при синтезі необхідно перевіряти величину кута тиску у тих положеннях механізму, в яких кут досягає максимальних значень (часто обмежуються робочим ходом). при
при  (рис. 7.2, а).
(рис. 7.2, а). . Зауважимо, що, як і у попередніх випадках, задача має багато розв’язків.
. Зауважимо, що, як і у попередніх випадках, задача має багато розв’язків.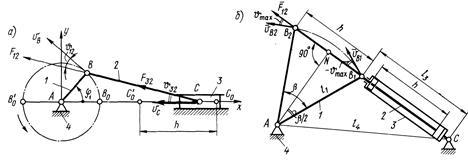
 визначається шляхом дослідження функції
визначається шляхом дослідження функції 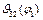 на максимум. Для центрального кривошипно-повзунного механізму максимальне значення кута тиску
на максимум. Для центрального кривошипно-повзунного механізму максимальне значення кута тиску  буде при
буде при  . Таким чином, при менших розмірах механізму (менші значення
. Таким чином, при менших розмірах механізму (менші значення  ) збільшується кут тиску, і відповідно, незалежно від того, яка ланка є ведена, зростає зусилля між повзуном та напрямною. Тому відношення
) збільшується кут тиску, і відповідно, незалежно від того, яка ланка є ведена, зростає зусилля між повзуном та напрямною. Тому відношення 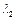 треба вибирати в певних межах, наприклад, для механізмів двигунів внутрішнього згоряння
треба вибирати в певних межах, наприклад, для механізмів двигунів внутрішнього згоряння  .
. два рази за період (
два рази за період ( ) приймає максимальне значення, що дорівнює 900. Ці положення кривошип проходить лише завдяки інерції маси ланки 1, яка обертається.
) приймає максимальне значення, що дорівнює 900. Ці положення кривошип проходить лише завдяки інерції маси ланки 1, яка обертається. , але є близьким за значенням до цієї величини. Точне значення ходу повзуна можна визначити з трикутників АС1С/1, АС2С/2 (рис. 7.1, б)
, але є близьким за значенням до цієї величини. Точне значення ходу повзуна можна визначити з трикутників АС1С/1, АС2С/2 (рис. 7.1, б)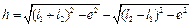 . (7.6)
. (7.6) і
і  можна визначити
можна визначити 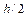 , та перевіряють рівність лівої та правої частини рівняння (7.6). Максимальний кут тиску
, та перевіряють рівність лівої та правої частини рівняння (7.6). Максимальний кут тиску  , якщо ж е< 0, то при
, якщо ж е< 0, то при  .
. . З
. З 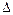 АВ1N одержимо формулу, що встановлює взаємозв’язок між кутом
АВ1N одержимо формулу, що встановлює взаємозв’язок між кутом  .
. .
.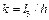 , допустимий кут тиску
, допустимий кут тиску 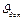 . Кут тиску в таких механізмах - кут між віссю циліндра за напрямком якої передається зусилля
. Кут тиску в таких механізмах - кут між віссю циліндра за напрямком якої передається зусилля 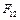 , та вектором швидкості
, та вектором швидкості  точки прикладання сили. Максимальний кут тиску
точки прикладання сили. Максимальний кут тиску  .
. . Відкладемо на продовженні прямої В2В1 відстань
. Відкладемо на продовженні прямої В2В1 відстань  і отримуємо шукані положення кінематичної пари С та довжину стояка
і отримуємо шукані положення кінематичної пари С та довжину стояка 


