
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення основних розмірів кулачкового механізмуСодержание книги
Поиск на нашем сайте
До основних розмірів кулачкового механізму відносяться: мінімальний радіус кулачка Кут тиску. Кут між нормаллю n-n у точці дотику взаємодіючих профілів вищої пари та вектором швидкості точки дотику вихідної ланки називається кутом тиску. При проектуванні механізмів з вищими парами величина цього кута має суттєве значення. Розглянемо кулачковий механізм зі штовхачем (рис. 8.4). Якщо знехтувати силою тертя у вищій кінематичній парі, то можна вважати, що сила тиску, з якою кулачок 1 діє на штовхач 2, направлена по спільній нормалі n-n в точці дотику ланок. Гострий кут, що утворений напрямом сили Розкладемо силу
Рис. 8.4 Кут тиску можна виразити через геометричні параметри кулачкового механізму
де
Подібною формулою виражається залежність між кутом тиску та основними параметрами коромислового кулачкового механізму. Аналіз цих залежностей свідчить, що при вибраному законі руху та зміщенні Отже, при проектуванні кулачкових механізмів основні розміри ‑ Таким чином, одним із найважливіших питань при проектуванні кулачкових механізмів є вибір допустимого кута тиску Рекомендовані такі значення допустимого кута тиску: Визначення основних розмірів кулачкових механізмів за заданим допустимим кутом тиску. Аналітичний метод визначення основних розмірів кулачкових механізмів із штовхачем (з вістрям або роликом) полягає у розв’язку рівняння (8.1) відносно шуканих параметрів при Розглянемо задачу графічного визначення Зауважимо, що у випадку механізму з роликовим штовхачем усі побудови є аналогічними, але в результаті буде знайдений Спочатку на основі попередньо побудованих графіків
Якщо величина зміщення задана
Рис. 8.5 Зауважимо, що в разі жорстких обмежень габаритних розмірів механізму беруть до уваги той факт, що небезпека заклинювання штовхача з силовим замиканням вищої пари має місце лише на фазі віддалення, оскільки при опусканні штовхач рухається під дією пружини (сили тяжіння). У цьому випадку при нереверсивному режимі роботи дотичну І-І проводять через т. А0. У кулачкових механізмах з геометричним замиканням вищої кінематичної пари умова Така геометрична інтерпретація співвідношення (8.1) використовується і для графічного визначення габаритних розмірів кулачкових механізмів з коромислом. Визначення мінімального радіуса кулачка за умовою опуклості профілю. Для кулачкових механізмів із плоским штовхачем при будь-якому положенні кулачка кут тиску є сталим. Зокрема, якщо тарілка перпендикулярна до осі штовхача (найрозповсюдженіший випадок), кут тиску дорівнює нулю. Отже, при проектуванні таких механізмів кут тиску не може бути покладений в основу визначення Профіль кулачка буде опуклим, якщо радіус кривини профілю в будь-якій точці буде більшим за нуль,
Рис. 8.6
Нерівність (8.2) дозволяє графічно визначити величину До цієї діаграми, на ділянці, що відповідає максимальному від’ємному значенню під кутом 450 до осі ординат проводиться дотична I-I. Згідно з нерівністю (8.2), за центр обертання кулачка може бути вибрана будь-яка точка, що розміщена нижче за точку перетину дотичної з віссю ординат. Наприклад, на рис. 8.6, а точка О1, тоді мінімальний радіус є відрізок А0О1, а його величина визначається за формулою Зауважимо, що в кулачкових механізмах з плоским штовхачем застосування ексцентриситету є недоцільним, оскільки призводить до збільшення габаритів механізмів.
8.5. Побудова профілю кулачка
Однією із основних задач синтезу кулачкових механізмів є побудова профілю кулачка. Розрізняють кінематичний та динамічний синтез кулачкових механізмів. При кінематичному синтезі значення Розглянемо послідовність побудови профілю кулачка, якщо задані: схема кулачкового механізму; максимальний хід та закон руху вихідної ланки; фазові кути; напрям обертання кулачка; мінімальний радіус кулачка. В основі графічного методу побудови профілю кулачка лежить метод обернення руху. Центральний кулачковий механізм (рис. 8.2, а). Вважається, що згідно з заданим законом руху попередньо побудована діаграма Побудову профілю кулачка виконують у такій послідовності (обернено до порядку побудови діаграми переміщення штовхача при кінематичному аналізі механізму, 8.2): 1. Із довільної точки О1 (вважаючи її центром обертання кулачка) проводимо коло радіусом 2. З точки О1 проводимо вертикальну пряму О1С, яку приймаємо за лінію руху штовхача. Точка перетину прямої О1С з колом 3. Користуючись діаграмою переміщень, розмічаємо шлях т. А вістря штовхача 4. Від прямої О1С в напрямі, протилежному напряму обертання кулачка, відкладемо фазові кути 5. Переносимо за допомогою циркуля миттєві положення точки А—А1, А2, А3, …, А12 на відповідні промені, і отримуємо на них точки 1/, 2/, 3/,…13 /- положення т. А вістря штовхача у відносному русі. Інколи для знаходження даних точок рекомендують безпосередньо з діаграми
6. З’єднавши ці точки плавною кривою, одержимо частину профілю кулачка на кутах 7. У випадку, якщо штовхач закінчується роликом, то отриманий профіль – центровий. Використовуючи центровий профіль як геометричне місце центрів ролика у відносному русі, будуємо дійсний профіль. Дійсний профіль одержимо як обгинну сім’ю дуг радіуса Позацентровий кулачковий механізм з роликовим штовхачем. Вважаємо, що згідно з заданим законом руху попередньо накреслено графік функції Побудову профілю кулачка виконують у такій послідовності. 1. З довільної точки О1 проводимо у вибраному масштабі 2. Дотично до кола радіуса 3. Від т. А0 вздовж лінії у-у відкладаємо переміщення штовхача А1, А2, А3,…, згідно графіка переміщень 4. З’єднаємо т. А0 з центром обертання кулачка О1. Від прямої А0О1 в напрямі, протилежному напряму обертання кулачка, відкладемо фазові кути
Рис. 8.7 5. З центра О1 радіусами О1А1, О1А2, О1А3,… проведемо концентричні дуги до перетину з відповідними дотичними. Точки перетину 1/, 2/, 3/, … являють собою положення ролика у відносному русі. З’єднавши ці точки плавною кривою, одержимо центровий профіль кулачка. 6. Проводимо ряд дуг радіусом Вибір радіуса ролика. Для забезпечення руху вихідної ланки механізму за заданим законом необхідно, щоб радіус ролика був менший за радіус кривини в будь-якій точці центрового профілю кулачка
де Окрім того, радіус ролика обмежують умовою При проектуванні кулачкових механізмів радіус ролика приймають таким, щоб забезпечити виконання наведених умов. При цьому конкретне значення призначають відповідно до стандартного ряду лінійних розмірів. Кулачковий механізм з тарілчастим штовхачем (рис. 8.1, в). Побудова профілю даного механізму виконується аналогічно (включно по п .5) до описаної вище побудови профілю центрального кулачкового механізму зі штовхачем. Різниця є лише в останньому етапі. 6. Через точки 1/, 2/, 3/,…, 13/ проводимо перпендикуляри до відповідних променів (рис. 8.6, б). Дані перпендикуляри являють собою послідовні положення площини тарілки штовхача у відносному русі навколо кулачка. Обгинна крива перпендикулярів і буде дійсним профілем кулачка.
Зубчасті передачі Зубчасті передачі є найпоширенішими механічними передачами у сучасному машино- та приладобудуванні. Їх застосовують як у механізмах найточніших приладів, де розміри коліс вимірюються кількома міліметрами, так і в найпотужніших машинах із розмірами коліс до 10 м. Зубчасті передачі здатні працювати в різноманітних умовах із коловими швидкостями від зовсім малих до 150 м/с і більше. Зубчаста передача складається з двох рухомих ланок – коліс, на ободах яких розміщені зубці та стояка. Зубці коліс входять у зачеплення між собою і завдяки їхній взаємодії забезпечують передавання обертового руху від одного колеса до другого. Менше з двох спряжених коліс називають шестірнею, більше – колесом; термін "зубчасте колесо" належить до обох коліс передачі. Переважно зубчаста передача призначена для передавання обертового руху, але її можна використовувати і як передачу для перетворення обертового руху в поступальний (передача зубчасте колесо-рейка). Зубчасті передачі можуть використовуватись для передавання обертового руху між довільно розміщеними у просторі валами, мають високий К.К.Д. ( Порівняно з іншими механічними передачами зубчасті передачі мають такі переваги: сталість передатного відношення; високу надійність та довговічність роботи; великий діапазон навантажень та компактність конструкції; незначні навантаження на вали передачі таїхні опори. До недоліків зубчастих передач належать: порівняно високі вимоги до точності виготовлення та монтажу; шум при роботі з високими швидкостями; потреба у постійному змащуванні; неможливість безступеневої зміни передатного числа. У зв'язку з великою відмінністю умов використання зубчастих передач форма елементів зубчастих зачеплень та конструкції зубчастих коліс дуже різноманітні. Тому зубчасті передачі та колеса можна класифікувати за цілою низкою ознак. За формою профілю зубців розрізняють евольвентні зубчасті передачі, які є найбільш поширеними та неевольвентні передачі. До останніх відносять зубчасті передачі із круговим профілем зубців (передачі із зачепленням Новікова) та передачі із циклоїдальним профілем зубців, які здебільшого застосовують у приладах та годинникових механізмах. За взаємним розміщенням осей валів зубчасті передачі бувають: - із паралельними осями валів - циліндричні передачі зовнішнього зачеплення (рис. 9.1, а, б, в), передачі типу зубчасте колесо-рейка (рис. 9.1, г) та циліндричні передачі внутрішнього зачеплення (рис. 9.1, д); - із валами, осі яких перетинаються, - конічні зубчасті передачі (рис. 9.2, а, б); - із мимобіжними у просторі осями валів - гвинтові зубчасті передачі (рис. 9.2, в).
За розміщенням на ободі та формою зубців розрізняють передачі та колеса: прямозубі (див. рис. 9.1, а, г, д), косозубі (див. рис. 9.1, б), шевронні (див. рис. 9.1, в) та з круговими зубцями (див. рис. 9.2, б). За конструктивним оформленням зубчасті передачі бувають: закриті (розміщені у спеціальному корпусі та забезпечені постійним змащуванням) і відкриті (працюють без мастила або змащуються періодично). За коловою швидкістю зубчастих коліс передачі поділяють на тихо- (
Основна теорема зачеплення
Наведемо деякі визначення. Взаємообвідними називають такі криві, при коченні та ковзанні яких одна по одній точка їх дотику здійснює неперервний рух вздовж кожної кривої; або до яких у точці дотику завжди можна провести спільну нормаль. Поверхні елементів вищої кінематичної пари, що забезпечують передачу заданого закону руху, називають спряженими. Отже, спряжені профілі мають задовольняти певні вимоги. Основна теорема зачеплення встановлює взаємозв’язок між геометрією спряжених поверхонь та законом відносного руху елементів вищої кінематичної пари. Стосовно задач синтезу спряжених поверхонь (профілів) – закон відносного руху є заданим. Основною кінематичною величиною механізмів, через яку і задається закон руху, є передатна функція Нагадаємо, що передатним називається відношення кутової швидкості ведучого вала (колеса) до кутової швидкості веденого вала (колеса). Синтез механізмів з вищими парами полягає в знаходженні спряжених поверхонь по заданому закону їх відносного руху. Для розв’язку цієї задачі користуються основною теоремою зачеплення. Нехай передача обертового руху між двома осями Швидкості
План швидкостей механізму за цим рівнянням приведений на рис. 9.3, б. Відрізок
або
Рис. 9.3
Відзначимо, що постійним дотик профілів буде тільки тоді, коли проекції швидкостей Враховуючи, що Отже, передатна функція (число) u 12рівна
З подібності
Рівність (2) є основною теоремою зачеплення, яку можна сформулювати так: спільна нормаль у точці дотику елементів вищої пари кочення та ковзання ділить лінію центрів на частини, обернено пропорційні кутовим швидкостям. Цю теорему ще називають теоремою Вілліса. Деколи використовують іншу форму доведення. Розглядають проекції на нормаль абсолютних швидкостей
або враховуючи, що отримаємо Точка Р, що ділить лінію центрів О 1 О 2 на частини, обернено пропорційні кутовим швидкостям, є миттєвим центром обертання у відносному русі ланок 1 і 2, в теорії зачеплення називається полюсом зачеплення. Радіуси Згадаємо теоретичну механіку. Нерухомою центроїдою називають геометричне місце миттєвих центрів обертання, тобто, положень т. Р на нерухомій площині. Рухомою центроїдою називають геометричне місце миттєвих центрів швидкостей у площині, яка зв’язана з рухомою плоскою фігурою. При русі плоскої фігури у її площині рухома центроїда котиться без ковзання по нерухомій. Обернена теорема про центроїди свідчить, що будь-який рух плоскої фігури в її площині можливо здійснити шляхом кочення без ковзання рухомої центроїди по нерухомій. Миттєвий центр швидкостей Р є точка плоскої фігури, швидкість якої у даний момент дорівнює нулю. Вона визначається як точка перетину перпендикулярів, проведених з будь-яких двох точок фігури до векторів швидкостей цих точок. У кожний момент часу з миттєвим центром швидкостей співпадає миттєвий центр обертання – точка нерухомої площини, поворотом навколо якої плоска фігура переміщується з одного положення у нескінченно близьке до нього. Знайдемо центроїди для розглядуваного випадку. По відношенню до ланки 1 ланка 2 має складний рух. Використовуючи метод обернення руху (зупинки) можна вказати напрями відносних швидкостей двох точок, наприклад Сукупність послідовних положень т. Р на нерухомій та рухомій площинах утворять, відповідно, рухому та нерухому центроїди. При змінному значенні передатної функції u 12 полюс зачеплення Р займає на лінії центрів О 1 О 2змінне положення. При сталому значенні u 12 полюс зачеплення розміщується в одній і тій же точці на прямій О 1 О 2; радіуси центроїд ланок 1 і 2 постійні. Отже, при передачі обертового руху між ланками з паралельними осями і постійним передатним відношенням центроїди представляють собою кола. В теорії зачеплення ці кола називаються початковими колами і позначаються Відзначимо також, що відносний рух зубчастих коліс представляють як кочення без ковзання одного початкового кола по іншому. Основною кінематичною умовою для профілів зубців зубчастих коліс є умова сталості миттєвого передатного числа. Основну теорему зачеплення стосовно зубчастих коліс формулюють ще так: для того, щоб передатне відношення за період зачеплення двох профілів зубців було сталим, необхідно, щоб нормаль до профілів у точці їх дотику, проходила через одну і ту ж точку на лінії центрів коліс та ділила лінію центрів у незмінному відношенні. Зауважимо також, що якщо полюс зачеплення Р розміщений між осями О 1і О 2, то ланки обертаються у різних напрямах, тобто u 12 має знак мінус, а зачеплення називається зовнішнім. Якщо полюс Р розміщується ззовні відрізка О 1 О 2, то ланки обертаються в однакових напрямах, передатне відношення має знак плюс, а зачеплення називається внутрішнім. Усі криві, що задовольняють основну теорему зачеплення, можуть бути використані для утворення бокових поверхонь зубців циліндричних передач. Отже, першою вимогою до кривих, якими окреслені профілі зубців, є відповідність профілів основній теоремі зачеплення. Цю умову задовольняють багато кривих. Однак профілі зубців повинні ще бути такими, щоб сприяти нескладному виготовленню зубчастих коліс з різним числом зубців, забезпечувати високий коефіцієнт корисної дії передачі, достатню міцність зубців, тощо. Цим вимогам найбільше відповідає евольвентне зачеплення і тому його найбільш широко застосовують у зубчастих передачах загального машинобудування. Евольвентне зачеплення, запропоноване Ейлером, має суттєві технологічні та експлуатаційні переваги: – простота побудови евольвентних профілів зубців; – виготовлення евольвентних коліс та інструменту для їх нарізання є найбільш простим, зокрема зубці можна нарізати інструментом рейкового типу з прямолінійним профілем; – допускається, в певних межах, відхилення міжосьової відстані (при неточності виготовлення, монтажу), при цьому зберігається постійним передатне відношення; – евольвентне зачеплення допускає виправлення (коригування) робочого профілю зубців із метою вибору оптимальних відрізків евольвенти, що забезпечує кращі характеристики передачі. Використовують інші види зачеплень (циклоїдальні, кругові, годинникові та інші). Серед “неевольвентних” зачеплень найбільше розповсюдження отримало зачеплення Новікова, яке характеризується високою міцністю зубців.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 365; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.119.128 (0.013 с.) |

 та зміщення
та зміщення 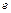 для механізму зі штовхачем; мінімальний радіус кулачка
для механізму зі штовхачем; мінімальний радіус кулачка  для механізму з коромислом.
для механізму з коромислом. тиску кулачка на штовхач і вектором швидкості штовхача називається кутом тиску
тиску кулачка на штовхач і вектором швидкості штовхача називається кутом тиску  . Зауважимо, що кут тиску є величиною змінною. Кут, що доповнює кут тиску до 900,називається кутом передачі (руху) (
. Зауважимо, що кут тиску є величиною змінною. Кут, що доповнює кут тиску до 900,називається кутом передачі (руху) ( ).
). та перпендикулярно до неї
та перпендикулярно до неї  . Сила
. Сила  - корисна сила, яка рухає штовхач; сила
- корисна сила, яка рухає штовхач; сила  - викликає перекошування штовхача в напрямній 3, внаслідок чого збільшуються реакції та сила тертя. Зрозуміло, що кулачковий механізм буде працювати тим краще, чим менший кут тиску. Не важко показати, що миттєвий коефіцієнт корисної дії кулачкового механізму зменшується зі зростанням кута тиску. При збільшенні кута тиску до деякого значення, що називається критичним
- викликає перекошування штовхача в напрямній 3, внаслідок чого збільшуються реакції та сила тертя. Зрозуміло, що кулачковий механізм буде працювати тим краще, чим менший кут тиску. Не важко показати, що миттєвий коефіцієнт корисної дії кулачкового механізму зменшується зі зростанням кута тиску. При збільшенні кута тиску до деякого значення, що називається критичним  , виникає явище заклинювання (самогальмування). Для нормальної роботи кулачкового механізму, кут тиску при будь-якому положенні кулачка має бути меншим за допустимий кут тиску, тобто
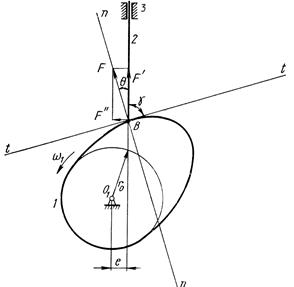
, виникає явище заклинювання (самогальмування). Для нормальної роботи кулачкового механізму, кут тиску при будь-якому положенні кулачка має бути меншим за допустимий кут тиску, тобто  .
.
 , (8.1)
, (8.1) – переміщення;
– переміщення;  ‑ аналог швидкості штовхача, що відповідає куту
‑ аналог швидкості штовхача, що відповідає куту 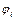 повороту кулачка від початку фази віддалення; e ‑ зміщення напрямної штовхача відносно центра кулачка. Відмітимо, якщо при русі штовхача на фазі віддалення вгору вздовж напрямної, остання зміщена відносно центра кулачка праворуч, то при його обертанні проти стрілки годинника зміщення підставляється в (8.1) зі знаком плюс, а при обертанні за годинниковою стрілкою - мінус. При зміщенні напрямної ліворуч від центра обертання кулачка знак
повороту кулачка від початку фази віддалення; e ‑ зміщення напрямної штовхача відносно центра кулачка. Відмітимо, якщо при русі штовхача на фазі віддалення вгору вздовж напрямної, остання зміщена відносно центра кулачка праворуч, то при його обертанні проти стрілки годинника зміщення підставляється в (8.1) зі знаком плюс, а при обертанні за годинниковою стрілкою - мінус. При зміщенні напрямної ліворуч від центра обертання кулачка знак  , тобто розмірів механізму.
, тобто розмірів механізму. або
або  (найпоширеніший випадок тарілки, перпендикулярної до напрямної) і r0 визначається з умови опуклості контуру.
(найпоширеніший випадок тарілки, перпендикулярної до напрямної) і r0 визначається з умови опуклості контуру.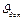 , від величини якого залежить розподіл сил у механізмі, його К.К.Д., габаритні розміри і т. ін.
, від величини якого залежить розподіл сил у механізмі, його К.К.Д., габаритні розміри і т. ін.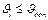 . В основі графічного методу також лежить залежність (8.1).
. В основі графічного методу також лежить залежність (8.1). , шляхом виключення параметра
, шляхом виключення параметра  , будуємо графік
, будуємо графік  , забезпечивши чисельно однакові масштаби по обох осях,
, забезпечивши чисельно однакові масштаби по обох осях,  (рис. 8.5). Для цього проводимо осі прямокутної системи координат. По осі ординат, в масштабі
(рис. 8.5). Для цього проводимо осі прямокутної системи координат. По осі ординат, в масштабі  , відкладемо від початку координат, згідно з графіком
, відкладемо від початку координат, згідно з графіком  переміщення штовхача (т. А0 відповідає нижньому початковому положенню штовхача, лежить на колі мінімального радіуса). Через отримані точки А0, А1, А2, …, проводимо прямі, паралельні осі абсцис та відкладаємо на них у масштабі
переміщення штовхача (т. А0 відповідає нижньому початковому положенню штовхача, лежить на колі мінімального радіуса). Через отримані точки А0, А1, А2, …, проводимо прямі, паралельні осі абсцис та відкладаємо на них у масштабі  , то проводять пряму y-y на відстані
, то проводять пряму y-y на відстані  від осі ординат (в масштабі
від осі ординат (в масштабі 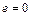 ) центр обертання кулачка буде знаходиться на продовженні лінії руху штовхача, нижче точки О1, а найменший радіус
) центр обертання кулачка буде знаходиться на продовженні лінії руху штовхача, нижче точки О1, а найменший радіус  .
.
 . Цю умову можна виразити нерівністю
. Цю умову можна виразити нерівністю . (8.2)
. (8.2)
 будується графік
будується графік  . По осі ординат відкладемо значення
. По осі ординат відкладемо значення  , а через отримані точки паралельно осі абсцис - відповідні значення
, а через отримані точки паралельно осі абсцис - відповідні значення  (рис. 8.6, а). Уся побудова виконується в одному масштабі
(рис. 8.6, а). Уся побудова виконується в одному масштабі 
 .
. переміщення штовхача (рис. 8.2, б).
переміщення штовхача (рис. 8.2, б). в його абсолютному русі, точки А1, А2, А3,..., А12. Для зручності побудови бажано, щоб вісь абсцис діаграми переміщень проходила через точку А0. Тоді ординати 1-1/, 2-2/, 3-3/,... діаграми переміщення безпосередньо визначають миттєві положення вістря штовхача.
в його абсолютному русі, точки А1, А2, А3,..., А12. Для зручності побудови бажано, щоб вісь абсцис діаграми переміщень проходила через точку А0. Тоді ординати 1-1/, 2-2/, 3-3/,... діаграми переміщення безпосередньо визначають миттєві положення вістря штовхача. . Ділимо кути
. Ділимо кути  на стільки ж рівних частин, на скільки вони поділені на діаграмі переміщення штовхача (8.2, б). Через точки поділу 1, 2, 3,…,13 на колі
на стільки ж рівних частин, на скільки вони поділені на діаграмі переміщення штовхача (8.2, б). Через точки поділу 1, 2, 3,…,13 на колі 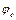 та
та  . Профілі кулачка, що відповідають фазовим кутам
. Профілі кулачка, що відповідають фазовим кутам 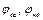 , будуть окреслені дугами кіл, які описані з т. О1 відповідно радіусами О16 / та О113 /. Таким чином, отримаємо дійсний профіль кулачка.
, будуть окреслені дугами кіл, які описані з т. О1 відповідно радіусами О16 / та О113 /. Таким чином, отримаємо дійсний профіль кулачка. , проведених з точок центрового профілю (рис. 8.7, б).
, проведених з точок центрового профілю (рис. 8.7, б). . Ділимо кути
. Ділимо кути 
 ,
, – мінімальний радіус кривини центрового профілю кулачка.
– мінімальний радіус кривини центрового профілю кулачка. .
.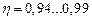 ), їх можна легко та зручно компонувати у окремі агрегати для серійного виробництва (редуктори), вони забезпечують достатній діапазон передаточних чисел (
), їх можна легко та зручно компонувати у окремі агрегати для серійного виробництва (редуктори), вони забезпечують достатній діапазон передаточних чисел ( ).
). Рис. 9.1.
Рис. 9.1.
 Рис. 9.2.
Рис. 9.2.
 м/с), середньо- (
м/с), середньо- ( м/с) та швидкохідні (
м/с) та швидкохідні ( м/с).
м/с). . Передатна функція зубчастих механізмів, як правило, стала і називається передатним відношенням,
. Передатна функція зубчастих механізмів, як правило, стала і називається передатним відношенням, 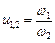 .
. та
та  (рис. 9.3, а) з кутовими швидкостями
(рис. 9.3, а) з кутовими швидкостями 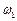 та
та  здійснюється за допомогою двох взаємообвідних профілів
здійснюється за допомогою двох взаємообвідних профілів  та
та  , що належать ланкам 1 та 2. Проведемо у точці дотику
, що належать ланкам 1 та 2. Проведемо у точці дотику  кривих
кривих  та нормаль
та нормаль  до цих кривих. Із точок
до цих кривих. Із точок  і
і  .
. та
та  точок
точок  та
та  , що належать ланкам 1 та 2, зв’язані умовою:
, що належать ланкам 1 та 2, зв’язані умовою: .
.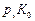 представляє собою нормальну складову
представляє собою нормальну складову  векторів швидкостей
векторів швидкостей  та
та  ,
,  та
та 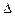
 маємо
маємо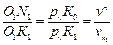 та
та  ,
, (1)
(1)
 ;
;  та підставляючи ці вирази в (1), отримуємо
та підставляючи ці вирази в (1), отримуємо 
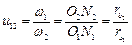 .
. та
та  маємо
маємо або
або  . (2)
. (2)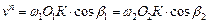 ,
,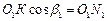 , а
, а  ,
, .
. і
і  та спільна дотична t-t до профілів. Звідси, миттєвий центр швидкостей Р знаходиться у точці перетину міжосьової віддалі О 1 О 2та спільної нормалі до профілів, яка проведена у точці контакту К.
та спільна дотична t-t до профілів. Звідси, миттєвий центр швидкостей Р знаходиться у точці перетину міжосьової віддалі О 1 О 2та спільної нормалі до профілів, яка проведена у точці контакту К. .
.


