
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кінематичний аналіз кулачкових механізмівСодержание книги
Поиск на нашем сайте
Кінематичне дослідження кулачкових механізмів полягає у визначенні закону руху вихідної ланки, тобто визначення залежності її переміщення, швидкості чи прискорення від часу або кута повороту кулачка, за відомими розмірами механізму, профілем кулачка і законом його руху. Розв’язок цієї задачі може бути виконаний графічним, графоаналітичним або аналітичним методами. Найчастіше застосовують графічний метод. Розглянемо побудову діаграми переміщення штовхача для кулачкового механізму, зображеного на рис. 8.2, а. Для цієї мети використовується метод обернення руху (інверсії), який дозволяє досить просто визначити відносне положення ланок механізму, без повторного викреслювання кулачка. Для цього всьому механізму в цілому умовно надається обертання з кутовою швидкістю кулачка, але в протилежному напрямі. Завдяки цьому кулачок зупиняється, а напрямна (стояк) разом зі штовхачем обертається з кутовою швидкістю Для наочності та більшої зручності побудови діаграми переміщень Знайдені переміщення т. А вихідної ланки дають можливість побудувати графік її руху (рис. 8.2, б). Для цього відкладемо на осі абсцис прямокутної системи координат, у деякому масштабі
Відмітимо, що з аналізу викладеного неважко зрозуміти порядок розв’язання основної задачі – синтезу кулачкового механізму, оскільки очевидно, що вона виконується у зворотному порядку. За допомогою таких же нескладних побудов, за винятком незначних особливостей, можна визначити положення вихідної ланки та одержати закон руху для кулачкових механізмів інших типів. Наприклад, у випадку механізму з роликовим штовхачем потрібно спочатку побудувати центровий профіль кулачка, після цього задача розв’язується аналогічно до розглянутої. Визначення швидкостей та прискорень. Дану задачу можна виконувати: методом кінематичних діаграм; методом планів; аналітичними методами; методом заміни кулачкового механізму важільним за наступним визначенням шуканих кінематичних параметрів для замінювального механізму. Якщо для кулачкового механізму визначені положення вихідної ланки та побудований графік Необхідно зазначити, що графічне диференціювання може привести до значних неточностей, особливо у випадку двократного диференціювання при визначенні прискорень. Застосування методу планів дає можливість отримати точніші кінематичні характеристики механізму. Для цього рекомендують перейти до замінювального механізму, тобто, вищу кінематичну пару IV класу замінити умовною ланкою та двома парами V класу. Далі задача розв’язується як для звичайного важільного механізму. Зауважимо, що кожному окремому положенню кулачкового механізму буде відповідати замінювальний механізм зі своїми розмірами ланок. Побудова планів швидкостей та прискорень для кулачкового механізму може бути виконана і без заміни вищих кінематичних пар нижчими, тобто, безпосередньо за дійсною схемою кулачкового механізму.
У разі потреби отримання точніших результатів застосовують аналітичні методи дослідження кулачкових механізмів (як з допомогою замінювальних механізмів, так і без них).
Закон руху вихідної ланки Під законом руху вихідної ланки кулачкового механізму розуміють залежність переміщення, швидкості чи її прискорення від часу. Закони руху вихідних ланок задаються, переважно, або аналітично у вигляді рівнянь, або графічно - у вигляді відповідних графіків. Оскільки в більшості випадків, що трапляються на практиці, рух кулачка відповідає рівномірному обертанню, то зручніше користуватися графіками, які являють собою залежність переміщення, аналога швидкості, чи аналога прискорення від кута повороту кулачка. Закон руху вихідної ланки визначається профілем кулачка і є основною характеристикою механізму. У практиці проектування кулачкових механізмів найбільше поширення отримали відносно прості, типові закони руху, наприклад, зображені на рис. 8.3 (для фази віддалення штовхача): а - лінійний; б - параболічний; в - косинусоїдальний; г - синусоїдальний; д, е - описані поліномами. Теоретично, кулачкові механізми можуть забезпечити будь-які закони руху вихідної ланки. Але на практиці користуються лише тими, які мають просту технологію обробки профілю кулачка та є сприятливими з точки зору динаміки роботи механізму. Від закону руху залежать динамічні та вібраційні властивості кулачкового механізму; він повинен бути таким, щоб зусилля, які виникають при русі, не впливали на точність відтворення передатної функції та не позначались на довговічності механізму. Розрізняють закони руху вихідної ланки кулачкових механізмів трьох видів: - з жорсткими ударами. Прикладом є лінійний закон (постійної швидкості, рис. 8.3, а). Швидкість руху штовхача на фазі віддалення постійна (прискорення дорівнює нулю), але на початку та в кінці фази швидкість має розрив. При миттєвій зміні швидкості штовхача прискорення, а отже, й сила інерції ланки, теоретично прямує до нескінченості, що є причиною жорстких ударів, і як наслідок - швидке спрацювання механізму. Такий закон допустимий лише в тихохідних механізмах при незначній масі штовхача (у випадку коли необхідно забезпечити постійну швидкість руху вихідної ланки); - з м’якими ударами. До цієї групи відносяться закони, при яких швидкість змінюється неперервно, а графік прискорення має точки розриву. Це характерно для параболічного, косинусоїдального законів руху (рис. 8.3, б, в, д). У точках розриву кривої прискорення сили інерції раптово змінюються на кінцеву величину, що викликає так званий м’який удар. М’який удар є менш небезпечний, ніж жорсткий удар, проте робота механізму у цьому випадку також супроводжується вібраціями, шумом та підвищеним спрацюванням. Цей закон використовують при помірних швидкостях; - без ударів. До безударних відносяться закони, при яких прискорення є неперервною функцією (рис. 8.3, г, е). Це закони, задані діаграмами прискорення, окресленою за синусоїдою, трикутником, трапецією та інші. При плавних кривих зміни прискорення удари теоретично відсутні (якщо похибки виготовлення профілів незначні). Такі закони рекомендують використовувати у швидкохідних механізмах. Недоліком їх є повільне наростання переміщення веденої ланки.
Найбільше використання мають кулачки, які забезпечують плавну зміну прискорення штовхача. Зауважимо, що при проектуванні кулачкових механізмів доцільно виходити з графіка прискорень – за ним можна зробити висновки про удари, шум, вібрації кулачкових механізмів, у той час, як за графіками переміщень важко судити про закон руху, оскільки криві переміщення зовні мало відрізняються. Графіки швидкості та переміщення в таких випадках знаходяться методом графічного інтегрування. Наголосимо, що не існує єдиного універсального критерію, який би враховував повний комплекс факторів, пов’язаних з вибором закону руху вихідної ланки кулачкового механізму. При оцінці ефективності профілю кулачка встановлюють комплекс заданих умов і обмежень, враховуючи їх вагомість.
Рис. 8.3
|
|||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 337; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.27.117 (0.009 с.) |

 (миттєві положення С1, С2, С3, …). У такому випадку визначення переміщення штовхача значно спрощується. Для цього проведемо мінімальним радіусом
(миттєві положення С1, С2, С3, …). У такому випадку визначення переміщення штовхача значно спрощується. Для цього проведемо мінімальним радіусом  основне коло. Відкладемо фазові кути. Поділимо кути віддалення
основне коло. Відкладемо фазові кути. Поділимо кути віддалення 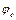 та опускання
та опускання  на довільне число рівних частин. Точки поділу 1, 2, 3 … нумерують відповідно до напрямку оберненого руху. За початкове положення прийнято положення, при якому вістря штовхача т. А займає крайнє нижнє положення А0. Через точки 1, 2, 3 …з центра О1 кулачка проведемо промені до перетину з профілем кулачка в точках 1/, 2/, 3/,… Продовження цих променів за профіль кулачка являють собою миттєві положення штовхача у його оберненому русі відносно кулачка. Переміщення вихідної ланки
на довільне число рівних частин. Точки поділу 1, 2, 3 … нумерують відповідно до напрямку оберненого руху. За початкове положення прийнято положення, при якому вістря штовхача т. А займає крайнє нижнє положення А0. Через точки 1, 2, 3 …з центра О1 кулачка проведемо промені до перетину з профілем кулачка в точках 1/, 2/, 3/,… Продовження цих променів за профіль кулачка являють собою миттєві положення штовхача у його оберненому русі відносно кулачка. Переміщення вихідної ланки  в кожному з положень є відстанню від
в кожному з положень є відстанню від  інколи рекомендують з центра О1 через точки 1/, 2/, 3/… провести дуги до перетину їх з лінією А0С руху штовхача. Одержимо точки А0, А1, А2,…, що зображають відносні положення т. А вістря штовхача при обертанні кулачка, тобто переміщення штовхача.
інколи рекомендують з центра О1 через точки 1/, 2/, 3/… провести дуги до перетину їх з лінією А0С руху штовхача. Одержимо точки А0, А1, А2,…, що зображають відносні положення т. А вістря штовхача при обертанні кулачка, тобто переміщення штовхача. , фазові кути
, фазові кути  (кут
(кут  можна відкладати без масштабу). Далі ділянки осі абсцис, які відповідають кутам
можна відкладати без масштабу). Далі ділянки осі абсцис, які відповідають кутам  , поділимо на таке ж число частин, на яке поділені відповідні кути на кулачкові. З точок поділу вздовж вертикалей в деякому масштабі
, поділимо на таке ж число частин, на яке поділені відповідні кути на кулачкові. З точок поділу вздовж вертикалей в деякому масштабі  відкладемо відповідні переміщення штовхача
відкладемо відповідні переміщення штовхача  . З’єднавши плавною кривою кінці ординат, отримаємо діаграму переміщення штовхача залежно від кута повороту кулачка
. З’єднавши плавною кривою кінці ординат, отримаємо діаграму переміщення штовхача залежно від кута повороту кулачка  . Як відомо, при обертанні кулачка з постійною кутовою швидкістю, діаграма
. Як відомо, при обертанні кулачка з постійною кутовою швидкістю, діаграма  , якщо від масштабу
, якщо від масштабу  .
.



