
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функція положень та кінематичні передатні функції механізмуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
До числа кінематичних характеристик відносяться також і ті, що не залежать від закону руху початкових ланок (часу), а визначаються лише будовою механізму, розмірами його ланок і, в загальному випадку, залежать від узагальнених координат механізму. Це функції положень та кінематичні передатні функції. Досить часто при проектуванні механізмів дійсний закон руху початкової ланки вдається визначити лише на наступних стадіях проектування, після динамічного аналізу. У таких випадках вводять кінематичні передатні функції, що не залежать від часу. А кінематичне дослідження виконується в два етапи - спочатку встановлюються залежності кінематичних параметрів ланок від узагальненої координати, тобто визначаються відносні функції (функції положення та кінематичні передатні функції механізму). І тільки після визначення закону руху початкової ланки знаходять залежності кінематичних параметрів вихідних і проміжних ланок від часу. Функція положень механізму. Функцією положень будь-якої ланки механізму називають залежність координати, що відображає положення даної ланки, від узагальненої координати і геометричних параметрів механізму. Функція положень вихідної ланки є функцією положення механізму. Тобто це залежність φ3 =φ3 (φ1) для третьої ланки механізму на рис. 2.1, або в загальному вигляді φn =φn (φ1) при обертальному русі n –ої ланки; при поступальному русі ланки, наприклад, ланки 5 механізму на рис. 1.3, г – залежність sF = sF (φ1). Треба зазначити, що в загальному випадку механізму з декількома ступенями вільності функція положень механізму є функцією усіх узагальнених координат φn=φn (φ1, φ2, …,φs), де φ1, φ2, …,φs - узагальнені координати механізму. Отже, функція положень є геометричною характеристикою механізму, яка не залежить від закону руху початкової ланки (часу, абсолютних значень швидкостей ланок і т.ін.) і визначається лише структурною схемою механізму та розмірами його ланок. Також відзначимо, що функція положень навіть для найпростіших важільних механізмів виражається складними рівняннями. Однак одержати її у графічній формі розміткою траєкторій неважко. Зупинимося на цій задачі нижче. Перша та друга кінематичні передатні функції механізму. Диференціюючи двічі функцію положень по узагальненій координаті, отримаємо вирази
Одержані функції φ/n, s/n, і φ//n, s//n є геометричними характеристиками n -ої ланки механізму і називаються, відповідно, першою та другою передатними функціями механізму. Або s/n –кінематична передатна функція швидкості точки (аналог швидкості); φ/n - кінематична передатна функція кутової швидкості ланки (аналог кутової швидкості або передатне відношення); s//n, φ//n, - відповідно передатна функція прискорення або кутового прискорення (аналог прискорення точки або аналог прискорення ланки). Встановимо зв’язок між вказаними геометричними та кінематичними характеристиками механізму з одним ступенем вільності при обертальному русі n -ої ланки. Продиференціюємо функцію положення за часом
тобто, де ω1, ωn - кутові швидкості відповідно ланок 1 та n; Як бачимо, функція З допомогою другої похідної функції положення за часом визначають кутовіприскорення ланок механізму
Якщо ω 1=const, ε1=0, то Таким чином, дійсна кутова швидкість n -ої ланки механізму дорівнює добутку кутової швидкості ω1 початкової ланки на першу передатну функцію (передатне відношення un 1); помноживши другу передатну функцію на ω12 (при ω1=const), дістанемо, відповідно, прискорення n -ої ланки. Фізичний зміст передатних функцій такий: перша При поступальному русі ланки викладки аналогічні:
Якщо ω 1=const, ε1=0, тоді Передатні функції швидкості та прискорення мають розмірність довжини, кутові передатні функції є безрозмірними величинами.
Оскільки для даної кінематичної схеми механізму передатні функції залежать лише від узагальненої координати і не залежать від закону руху початкової ланки, то кінематичне дослідження можна виконувати суто геометричними методами. Передатні функції дозволяють легко порівнювати закони руху ланок, а отже і знаходити оптимальні параметри механізму за заданими умовами роботи. Кінематичне дослідження за допомогою передатних функцій є ефективним у випадку кількох можливих рухів початкової ланки. Якщо при проектуванні чи дослідженні механізму задана чи визначена функція положення або одна з передатних функцій механізму, то інші залежності можуть бути встановлені методами диференціювання чи інтегрування як числовими, так і графічними.
Плани механізму
Визначення переміщень, положень ланок і траєкторій, що описують окремі точки ланок, тобто розв’язання першої основної задач кінематики, можна виконати графічними або аналітичними методами. Досить широко використовується графічний метод - за допомогою побудови планів механізму. Зображення кінематичної схеми механізму у вибраному масштабі при відповідному положенні початкової ланки називається планом механізму. Графічне розв’язування задач теорії механізмів потребує зображення різноманітних фізичних величин (шляху, довжин ланок, швидкостей, прискорень, сил і т. ін.) у вигляді ліній тієї чи іншої довжини. Для цього користуються масштабним коефіцієнтом. Масштабний коефіцієнт (масштаб) є відношення дійсного значення зображуваної величини до довжини відрізка, який цю величину зображує на кресленні. Масштаб позначається літерою μ з індексом того параметра, який зображується графічно.
Таким чином, масштаб довжини – це відношення натурального розміру ланки в метрах до довжини відрізка в міліметрах, який зображує цю ланку на кресленні (плані механізму), При виборі масштабу рекомендують дотримуватися стандартних креслярських масштабів, а також міркувань зручності підрахунків та наочності зображення. Наприклад, масштабу М1:1 відповідає масштабний коефіцієнт μl = 0,001м/мм, масштабу М1:2 відповідає μl=0,002м/мм і т.ін. Для побудови планів механізму повинні бути задані розміри всіх його ланок, а якщо будується одне конкретне положення механізму і положення початкової ланки. У русі більшості механізмів спостерігається циклічність, при цьому усі кінематичні параметри механізмів змінюються періодично. Тому, зазвичай, при дослідженні механізмів будують ряд послідовних положень механізму. При виконанні курсових проектів, як правило, кінематична схема механізму будується для 12 положень.
Послідовність побудови планів механізму: - вибирають масштаб побудови - знаходять довжини відрізків, якими на кресленні зображатимуться ланки (рис. 2.1– - перш за все, на креслення наносять положення нерухомої ланки (намічаються нерухомі точки механізму, наносяться, при наявності, нерухомі напрямні; на рис. 2.1 - т. О1, С); - викреслюють задане положення початкової ланки. Якщо будується n планів механізму, то знаходять початкові (“мертві”, крайні) положення механізму і, відповідно, початкової ланки;
- лише після цього викреслюють групи Ассура в порядку їх приєднання при утворенні механізму. Наголосимо, що доцільно за початкове положення механізму (кривошипа) вибрати те, яке відповідає одному з крайніх положень вихідної ланки (ланки, до якої прикладена сила корисного опору, або рушійна сила). У кривошипно-повзунному механізмі чи шарнірному чотириланковику (або якщо вони лежать в основі розглядуваних механізмів) вихідна ланка перебуватиме у крайніх положеннях, коли кривошип накладатиметься на шатун, або витягуватиметься в одну лінію з ним. У кулісному механізмі вихідна ланка (куліса СД, рис. 1.3, в) перебуватиме у крайніх положеннях, коли кривошип АВ і куліса утворять прямий кут. Зазначимо, що з двох крайніх положень механізму за початкове вибирають те, що відповідає початку робочого ходу. Оскільки в більшості машин робочий хід здійснюється повільніше (рівномірніше) ніж холостий, то він відповідає руху кривошипа з одного крайнього положення до іншого через більший з центральних кутів. Більший з центральних кутів, що описує кривошип при русі механізму з одного крайнього положення до іншого, називається кутом робочого ходу. Розглянемо побудову 12 планів механізму на прикладі шарнірного чотириланковика, структурна схема якого зображена на рис. 1.3, а. Виконуємо перші три пункти наведеної вище послідовності побудови планів. Після цього, радіусом О1А (рис. 2.1) проводимо коло з центром у т. О1, яке є геометричним місцем миттєвих положень т. А кривошипа 1. Як відомо, закон руху початкової ланки в загальному випадку задається у вигляді рівняння
Для визначення положення ланок 2 і 3 достатньо встановити положення кінематичної пари В, що шарнірно з’єднує ці ланки між собою. Для цього умовно роз’єднуємо шарнір у т. В і розглядаємо можливі рухи цієї точки. Оскільки нерухомий центр обертання С займає цілком певне положення, то т. В, яка знаходиться на сталій відстані ВС від т. С, може описати тільки дугу Отже, якщо потрібно побудувати, наприклад, 3 -тє положення механізму, то з точки А3 радіусом R=AB робимо засічку на дузі Якщо до складу механізму входять декілька груп Ассура, то їх плани будуються аналогічно. На планах механізму, у разі необхідності, можна побудувати траєкторії, що описують окремі точки ланок. Траєкторії різних точок шатуна мають різноманітну форму, оскільки шатун здійснює плоскопаралельний рух. Траєкторії точок, що розміщені на ланках, які здійснюють плоскопаралельний рух, називають шатунними кривими. Точність побудованої траєкторії залежить від вибраного числа положень механізму і масштабу
Рис. 2.1
Зазначимо, що залежно від вибору положення точки (F, E, K, Н, G) на шатуні отримуються різні шатунні криві (рис. 2.2). Окремі ділянки деяких кривих мало відрізняються від прямих або дуг кіл. Ці ділянки можуть бути використані для спрямляючих механізмів або механізмів із зупинками. Шатунні криві в сучасній техніці широко використовуються для виконання певних рухів робочих органів різних машин і механізмів. Наприклад, у механізмі сіноворушилки, в тістомісильній машині і т.ін. Подібно будуються плани механізму (кінематичні схеми) інших важільних механізмів другого класу.
Рис. 2.2 При побудові планів механізмів, що мають триповодкові групи, також може бути використаний метод перетину двох траєкторій відносного руху (спосіб засічок). Цей спосіб в розглядуваному випадку ще називають способом удаваних положень або геометричних місць. Оскільки такий метод побудови є досить трудомістким, часто користуються шаблоном, який має форму базисної ланки.
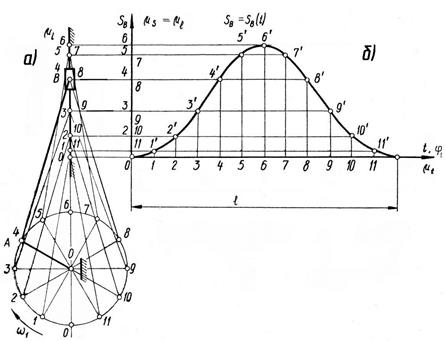
У випадку механізмів з вищими кінематичними парами (наприклад, кулачковими) доводиться враховувати, що профілі, або один з них, мають складні контури. Викреслювання послідовно декількох складних профілів є трудомісткою процедурою. У цих випадках доцільно застосувати метод обернення руху (метод інверсії). Суть його полягає в тому, що всьому механізмові (разом зі стояком) надають обертання з кутовою швидкістю, яка дорівнює за величиною, але протилежна за напрямом кутовій швидкості ланки, що має складний профіль (кулачок). Таким чином, рухому ланку зі складним контуром умовно роблять нерухомою; це дозволяє викреслювати її лише один раз. Відносне положення усіх ланок при цьому не змінюється. Приклад використання методу обернення руху буде розглянуто при вивченні кулачкових механізмів. При побудованих планах механізму неважко побудувати діаграми переміщення та отримати функції положень ланок механізму. Побудова діаграм переміщення. При дослідженні механізмів будують діаграми лінійних або, при коливальному русі ланки, кутових переміщень. Розглянемо побудову графіка sB(t) переміщень повзуна В кривошипно-повзунного механізму (рис. 2.3): - викреслюють 12 рівновіддалених за кутом повороту кривошипа планів механізму в масштабі - будують прямокутну систему координат. На осі абсцис відкладають відрізок l, що в масштабі - ділять відрізок l на 12 рівних частин. Від точок поділу 1, 2, 3, …11, паралельно осі ординат, відкладають відрізки 1-1/, 2-2/, 3-3/,..., які у вибраному масштабі З’єднавши одержані точки 0, 1/, 2/,…11/ плавною кривою, отримують діаграму переміщень повзуна, sB(t). Оскільки у задачах кінематики прийнято рух кривошипа рівномірним (за однакові проміжки часу він повертається на рівні кути), то можна вважати, що по осі абсцис відкладено і час t і кут повороту кривошипа
Рис. 2.3
2.4. Дослідження руху механізмів методом
Якщо один з кінематичних параметрів механізму заданий у вигляді графіка чи таблиці значень, то в цьому випадку ефективними є графічні або чисельні методи диференціювання та інтегрування. Зазначимо, що при експериментальному дослідженні такі графіки викреслюються за допомогою самописних приладів. Задачі дослідження закономірності зміни переміщень, швидкостей і прискорень за повний цикл (період) руху досліджуваного механізму простіше розв’язуються за допомогою кінематичних діаграм (графіків руху). У практичних задачах ТММ кожна кінематична діаграма - це графічне зображення зміни одного з кінематичних параметрів ланки: переміщення, швидкості або прискорення як функції від часу або переміщення початкової ланки механізму (як функції від узагальненої координати). Наприклад, у випадку кривошипно-повзунного механізму для т. В повзуна (рис. 2.3) - це залежності sB(t), vB(t), aB(t) або sB( Розглядуваний метод дозволяє при заданій будь-якій з цих діаграм без значних зусиль отримати інші. Методом кінематичних діаграм часто користуються для наочності та виявлення можливих помилок при обчисленні. Переваги цього методу – простота у використанні й те, що результатом є наочне графічне зображення зміни одного з кінематичних параметрів руху від часу чи узагальненої координати. Варто мати на увазі, що методи графічного диференціювання та інтегрування не завжди можуть забезпечувати достатню точність результатів. Зазначимо, що до графічного диференціювання та інтегрування необхідно деколи звертатись навіть у тих випадках, коли кінематична функція задана аналітично, але не має достатньо простих формул для визначення похідної чи інтеграла. Графічне диференціювання. Метод дотичних. Графічне диференціювання використовується, коли є графік функції, а потрібно отримати графік її похідної. Так, наприклад, побудовано графік переміщення повзуна кривошипно-повзунного механізму (рис. 2.3), а необхідно побудувати графіки швидкості, прискорення. Розглянемо теоретичні основи графічного диференціювання. Використаємо відому залежність v = Нехай крива АВ (рис. 2.4) є графік деякої функції
Проведемо з точки 1// пряму, паралельну осі 0х, до перетину з ординатою т. М1. Ордината точки перетину 1/ і дає значення похідної Таким чином, для того, щоб побудувати графік похідної за графіком функції, поділимо ділянку АВ, заданої кривої, на деяке число частин. Далі, розглянутим методом, неважко знайти у точках поділу заданої кривої значення похідної - тобто точки диференціальної кривої. З’єднавши отримані точки плавною кривою, дістанемо графік функції
Рис. 2.4 Диференціювання методом дотичних має відносно низьку точність, оскільки досить складно проводити дотичні до кривих. Більшого поширення набув метод хорд, який відрізняється більшою точністю. Відмінність методу хорд полягає лише у тому, що значення похідної функції знаходять не у точках поділу кривої, а у точках, що ділять навпіл кожний з інтервалів (рис. 2.5, точки Зазначимо, що графік похідної буде точнішим при більшій кількості частин поділу кривої. Інтервали не обов’язково повинні бути рівними між собою; їх розмір вибирається з урахуванням того, щоб відповідні частини кривої менше відхилялись від прямої. Особливу увагу треба звернути на ділянки, де крива, яку диференціюють, має екстремуми; ділянки, у яких лінія значно звивається, слід розбивати на більше число частинок. Масштаби при графічному диференціюванні. Припустимо, що задана крива (рис. 2.5) зображає діаграму переміщень,
Рис. 2.5
Підставимо в (2.1) де
або в загальному випадку масштаб диференціальної кривої Послідовність диференціювання методом хорд. Задано діаграму переміщення кривошипно-повзунного механізму (рис. 2.6, а). Побудуємо діаграму швидкості: - на заданій кривій відмічають ряд точок 1/, 2/, 3/,…, які з’єднують хордами, тобто, замінюють задану криву ламаною лінією; - під діаграмою переміщень будуємо нову систему координат так, щоб осі абсцис були паралельними, а ординат - лежали на одній прямій (рис. 2.6, б). Ділимо вісь абсцис на такі ж інтервали, як і на попередньому графіку; - відкладаємо по осі абсцис ліворуч від початку системи координат довільний відрізок ОР1 - полюсну відстань;
Рис. 2.6. - з точки Р1 проводимо промені Р11//, Р12//, Р13//,..., паралельні до відповідних хорд кривої переміщень. Ці промені відтинають на осі ординат відрізки 01//, 02//, 03//,..., що пропорційні середній швидкості повзуна посередині відповідних інтервалів часу; - перенесемо точки 01//, 02//, 03//,..., на середини ординат відповідних ділянок. З’єднаємо точки 0, 1/, 2/,... плавною кривою. Отримана крива і буде діаграмою швидкості. Маючи діаграму швидкості, аналогічно методом хорд будують, за потреби, діаграму прискорень (рис. 2.6, в). Зазначимо, якщо діаграму переміщень задано у вигляді функції sB( Масштаби по осях ординат визначаються за формулами: – для діаграм швидкостей та прискорень – для діаграм аналогів швидкостей та прискорень де Н1, Н2 – відрізки в мм, взято з креслення (рис. 2.6). Масштаби по осях абсцис Порівнюючи графіки (рис. 2.6), можна встановити такий зв’язок між кінематичними діаграмами: - зростанню ординат кривої функції, що диференціюється, відповідають додатні значення ординат диференціальної кривої, а зменшенню – від’ємні значення; - екстремальним значенням функції (максимуми та мінімуми) відповідають нульові значення графіка похідної. - точкам перегину графіка функції відповідають екстремальні значення диференціальної кривої. Графічне інтегрування. Побудову графіків швидкості за заданим графіком прискорень та графіків переміщень - за графіком швидкостей виконують так званими прийомами графічного інтегрування. Існує декілька способів побудови інтегральної кривої: спосіб хорд, площ та інші. Розглянемо спосіб хорд. Інтегрування – це дія, обернена диференціюванню. Відповідно послідовність графічного інтегрування за способом хорд обернена послідовності диференціювання за цим способом. Нехай заданим є графік функції швидкості v(t). Знайдемо графік функції переміщення s(t).
|
|||||||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 593; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.117.89 (0.018 с.) |



 ,
, ,
, 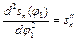 .
. ,
, ,
, .
.  є відношенням миттєвих швидкостей ланок; в загальному випадку її називають передатною функцією. Відношення
є відношенням миттєвих швидкостей ланок; в загальному випадку її називають передатною функцією. Відношення  називається передатним відношенням і позначається un 1. Відношення кутової швидкості однієї ланки до кутової швидкості другої ланки називається передатним відношенням, позначається буквою u, як правило, з цифровими індексами, що відповідають номерам розглядуваних ланок
називається передатним відношенням і позначається un 1. Відношення кутової швидкості однієї ланки до кутової швидкості другої ланки називається передатним відношенням, позначається буквою u, як правило, з цифровими індексами, що відповідають номерам розглядуваних ланок  . Передатне відношення є величиною безрозмірною. Це одна з основних характеристик механізмів передач.
. Передатне відношення є величиною безрозмірною. Це одна з основних характеристик механізмів передач.
 .
. .
. та друга
та друга 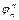 передатні функції являють собою відповідно швидкість
передатні функції являють собою відповідно швидкість  та прискорення
та прискорення  n- ої ланки механізму за умови, що
n- ої ланки механізму за умови, що  . Тому зазначені передатні функції називають також аналогами швидкостей та прискорень.
. Тому зазначені передатні функції називають також аналогами швидкостей та прискорень. ,
, .
. .
. Масштаб має розмірність: у чисельнику – розмірність зображуваної величини, а у знаменнику - мм (розмірність довжини відрізка на кресленні).
Масштаб має розмірність: у чисельнику – розмірність зображуваної величини, а у знаменнику - мм (розмірність довжини відрізка на кресленні). , де lAB - справжній розмір; AB - масштабний розмір на кресленні.
, де lAB - справжній розмір; AB - масштабний розмір на кресленні.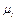 ;
;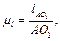 отже
отже 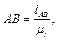
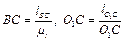 );
);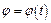 . В технічних задачах при кінематичному дослідженні механізмів закон руху початкової ланки беруть лінійним, тобто швидкість її руху вважають сталою (
. В технічних задачах при кінематичному дослідженні механізмів закон руху початкової ланки беруть лінійним, тобто швидкість її руху вважають сталою ( , дорівнює проектованій середній кутовій швидкості; в дійсності кривошип може обертатися нерівномірно, навіть із зупинками). Таким чином, за рівні проміжки часу кривошип повертається на рівні кути. При побудові 12 планів механізму коло, що описує т. А кривошипа, ділиться на 12 рівних частин, починаючи з початкового положення механізму. Для його знаходження з центра обертання кривошипа О1 досить зробити засічки радіусами R=АВ-О1А і R=О1А+АВ на траєкторії руху т. В - дузі α3-α3 (відповідно кривошип О1А накладатиметься на шатун АВ або витягуватиметься з ним в одну лінію). За початкове положення т. А візьмемо т. А0, яка відповідає початку робочого ходу (
, дорівнює проектованій середній кутовій швидкості; в дійсності кривошип може обертатися нерівномірно, навіть із зупинками). Таким чином, за рівні проміжки часу кривошип повертається на рівні кути. При побудові 12 планів механізму коло, що описує т. А кривошипа, ділиться на 12 рівних частин, починаючи з початкового положення механізму. Для його знаходження з центра обертання кривошипа О1 досить зробити засічки радіусами R=АВ-О1А і R=О1А+АВ на траєкторії руху т. В - дузі α3-α3 (відповідно кривошип О1А накладатиметься на шатун АВ або витягуватиметься з ним в одну лінію). За початкове положення т. А візьмемо т. А0, яка відповідає початку робочого ходу ( ), при заданому напрямі обертання кривошипа. Зрозуміло, що т.
), при заданому напрямі обертання кривошипа. Зрозуміло, що т.  не завжди збігається з точками поділу траєкторії т. А на рівні частини, послідовні положення якої позначені А0, А1, А2, …, 11.
не завжди збігається з точками поділу траєкторії т. А на рівні частини, послідовні положення якої позначені А0, А1, А2, …, 11. кола радіуса ВС. З іншого боку, внаслідок незмінності довжини шатуна АВ точка В може описати навколо т. А тільки дугу радіуса АВ. Таким чином, геометричним місцем можливих положень центра шарніра В є дві дуги кіл радіусів АВ та ВС. Точка перетину цих дуг і дасть дійсне положення т. В для конкретного положення кривошипа.
кола радіуса ВС. З іншого боку, внаслідок незмінності довжини шатуна АВ точка В може описати навколо т. А тільки дугу радіуса АВ. Таким чином, геометричним місцем можливих положень центра шарніра В є дві дуги кіл радіусів АВ та ВС. Точка перетину цих дуг і дасть дійсне положення т. В для конкретного положення кривошипа.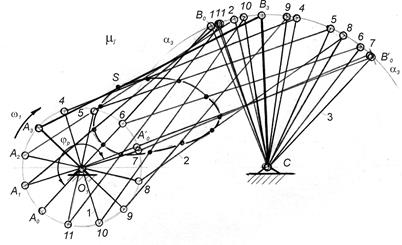

 ; за початок відліку прийнято нижнє крайнє положення повзуна;
; за початок відліку прийнято нижнє крайнє положення повзуна; зображає період Т одного оберту кривошипа, тобто
зображає період Т одного оберту кривошипа, тобто  ,
,  ;
; зображають переміщення повзуна від крайнього нижнього положення. Якщо переміщення відкладаються безпосередньо з планів механізму (як у прикладі на рис. 2.3), то
зображають переміщення повзуна від крайнього нижнього положення. Якщо переміщення відкладаються безпосередньо з планів механізму (як у прикладі на рис. 2.3), то  .
. . Тобто графік sB(t) одночасно є графіком sB(j1), який представляє собою функцію положення механізму. Масштаб
. Тобто графік sB(t) одночасно є графіком sB(j1), який представляє собою функцію положення механізму. Масштаб  цього графіка буде:
цього графіка буде:  , або
, або  .
.
 ,
,  або
або 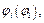
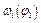 ,
,  .
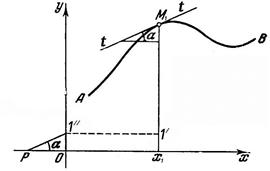
. . Геометрично, похідна функції визначається тангенсом кута нахилу дотичної до графіка функції, проведеної у точці, абсциса якої є точка диференціювання,
. Геометрично, похідна функції визначається тангенсом кута нахилу дотичної до графіка функції, проведеної у точці, абсциса якої є точка диференціювання, 
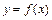 . Проведемо дотичну до графіка у т. М1, що відповідає заданій абсцисі
. Проведемо дотичну до графіка у т. М1, що відповідає заданій абсцисі 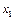 .Відкладемо на осі абсцис вліво від початку прямокутної системи координат відрізок ОР (полюсну відстань), що дорівнює одиниці масштабу. З точки Р (полюса) проведемо пряму, паралельну дотичній до перетину з віссю ординат. Відрізок 01// буде виражати значення похідної
.Відкладемо на осі абсцис вліво від початку прямокутної системи координат відрізок ОР (полюсну відстань), що дорівнює одиниці масштабу. З точки Р (полюса) проведемо пряму, паралельну дотичній до перетину з віссю ординат. Відрізок 01// буде виражати значення похідної 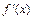 , при заданому значенні
, при заданому значенні 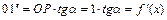
 .
.
 ). Перевагою є те, що при цьому замість дотичних беруться, як правило, з досить великою точністю, хорди, що з’єднують кінцеві точки кожного інтервалу. Метод ґрунтується на відомій теоремі про скінчений приріст функції: якщо функція, що задана графічно, та її перша похідна неперервні, то в будь-якому інтервалі хорда, що стягує дану дугу, паралельна дотичній до кривої, принаймні, в одній точці, яка лежить у середині цього інтервалу.
). Перевагою є те, що при цьому замість дотичних беруться, як правило, з досить великою точністю, хорди, що з’єднують кінцеві точки кожного інтервалу. Метод ґрунтується на відомій теоремі про скінчений приріст функції: якщо функція, що задана графічно, та її перша похідна неперервні, то в будь-якому інтервалі хорда, що стягує дану дугу, паралельна дотичній до кривої, принаймні, в одній точці, яка лежить у середині цього інтервалу. . Знаючи масштаб
. Знаючи масштаб 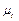 часу, для будь-якої точки М(х,у) кривої можна записати
часу, для будь-якої точки М(х,у) кривої можна записати  ,
, 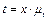 . Тоді
. Тоді . (2.1)
. (2.1)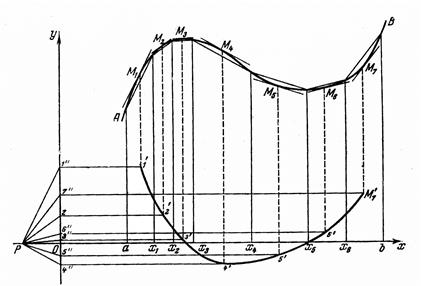
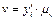 та
та 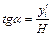 ,
, - відрізки 01//, 02//, 03//,..., які зображають в масштабі
- відрізки 01//, 02//, 03//,..., які зображають в масштабі 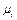 швидкості у відповідних положеннях механізму; Н – полюсна відстань ОР. Тоді масштаб графіка швидкості
швидкості у відповідних положеннях механізму; Н – полюсна відстань ОР. Тоді масштаб графіка швидкості  ,
, .
.
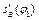 та прискорення
та прискорення  (аналогів швидкості та прискорення).
(аналогів швидкості та прискорення). ,
,  ,
,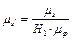 ,
,  ,
,


