
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Якісні показники зубчастої передачіСодержание книги
Поиск на нашем сайте
Розглянемо якісні показники зубчастої передачі, які дають можливість оцінити передачу у відношенні плавності та безшумності зачеплення, стійкості щодо можливого спрацювання, міцності зубців, а також порівняти ряд передач за цими показниками. Така оцінка важлива для раціонального призначення коефіцієнтів зміщення при проектуванні та виготовленні зубчастих передач. Коефіцієнт перекриття враховує неперервність, плавність, безшумність та безударність зачеплення. Такі якості передачі забезпечуються перекриттям роботи однієї пари зубців роботою іншої пари. Зубчасте зачеплення є багатопрофільним зачепленням, в якому спряжені пари зубців почергово входять у зачеплення. Тому перш ніж одна пара зубців вийде із зачеплення, необхідно, щоб друга пара обов’язково ввійшла в зачеплення. Про це судять за коефіцієнтом перекриття. Відношення кута торцевого перекриття зубчастого колеса до його кутового кроку називається коефіцієнтом перекриття ea. Отже, коефіцієнт перекриття прямозубої передачі ea= Кут торцевого перекриття ja – кут повороту зубчастого колеса від моменту входу зубця в зачеплення до моменту виходу його із зачеплення. Коефіцієнт перекриття повинен бути більшим за одиницю, інакше при роботі зубчастої передачі можуть виникнути моменти, коли у зачепленні не буде знаходитися жодна пара зубців і передача буде працювати з ударами. Із-за неточностей виготовлення та монтажу і внаслідок зношення величина коефіцієнта перекриття може виявитися меншою за розрахункову. Тому при проектуванні зачеплення найменшою допустимою величиною коефіцієнта перекриття вважають ea = 1,05, який забезпечить неперервність процесу зачеплення з 5% запасом. Але бажано, щоб значення коефіцієнта ea було якомога більшим. Коефіцієнт перекриття іноді називають коефіцієнтом плавності або тривалості зачеплення. Він визначає середнє число пар зубців, що одночасно знаходяться у зачепленні. Наприклад, якщо ea=1,7, це означає, що протягом 70% всього часу роботи передачі в зачепленні знаходяться дві пари зубців, а на протязі 30% – одна пара. Зі збільшенням коефіцієнта перекриття підвищується плавність роботи та несуча здатність передачі, зменшуються динамічні навантаження та шум передачі. Тому у швидкохідних та високонавантажених передачах замість прямозубих коліс (eamax £1,98 ) використовують косозубі чи шевронні колеса, або колеса з криволінійними зубцями, які забезпечують більші коефіцієнти перекриття (до 10 і більше). Коефіцієнт перекриття може бути визначений аналітично
де aа1, aа2 – кути профілю зубців у точці на колі вершин. Коефіцієнт питомого тиску враховує вплив геометрії зубців (радіусів кривини їхніх профілів) на величину контактних напружень, що виникають у місцях дотику профілів. Формулу Герца, що визначає величину контактних напружень, можна написати у вигляді
де Q – сила взаємодії зубців; У цій формулі тільки величина J залежить від геометрії профілів зубців. Коефіцієнтом питомого тиску називається відношення модуля до зведеного радіуса кривини евольвентних профілів у точці контакту J = Коефіцієнт J величина безрозмірна, що не залежить від модуля, оскільки r пропорційний модулю. Враховуючи, що J = При повороті зубчастих коліс та переміщенні точки контакту К по лінії зачеплення r 1 та r 2 суттєво змінюються, тому коефіцієнт J – функція положення точки контакту на лінії зачеплення. При розрахунку зубців на міцність особливо важливе значення має коефіцієнт Jp у полюсі зачеплення Р (всередині зони однопарного зачеплення) Jp = Коефіцієнт питомого тиску J зменшується (відповідно і контактні напруження) при збільшенні коефіцієнтів зміщення х 1, х2. При цьому зуби утворюються більш пологими ділянками евольвенти. Отже, конструктор може зменшувати контактні напруження, призначуючи відповідні коефіцієнти зміщення. Коефіцієнт ковзання. У точці контакту зубців, що перебувають у зачепленні, мають місце відносні перекочування та ковзання профілів. Ковзання профілів супроводжується тертям. Тертя є причиною втрат енергії та спрацювання робочих поверхонь. Швидкість vs ковзання профілів є одним із основних факторів, які визначають втрати Неважко показати, що швидкість ковзання спряжених профілів у вищій парі дорівнює добутку відстані між точкою контакту К та полюсом зачеплення Р на кутову швидкість
де Отже, швидкість ковзання у зачепленні пропорційна відстані точки контакту до полюса. У полюсі Швидкість ковзання збільшується зі зростанням висоти зубців, тобто їх модуля. У коліс із малим модулем та великим числом зубців ковзання менше, ніж у коліс із великим модулем та малим числом зубців. Проводити оцінку ковзання профілів у відносному русі тільки по величині швидкості ковзання недостатньо: необхідно ще враховувати швидкість руху точки дотику по кожному з профілів, тобто швидкостей Коефіцієнтами ковзання називають відношення швидкості ковзання
Коефіцієнт ковзання враховує вплив геометричних та кінематичних факторів на величину ковзання у процесі зачеплення.
Рис. 9.7 Розрахункові формули для коефіцієнтів ковзання
де На рис. 9.7 показані криві зміни коефіцієнтів ковзання вздовж лінії зачеплення. Детально побудову діаграм розглянемо на занятті з курсового проектування. Аналізуючи отримані епюри, можна констатувати: - відносне ковзання на ніжці зубця більше ніж на головці. Тому ніжка в евольвентному зубці зношується сильніше, ніж головка; - при наближенні до основного кола відносне ковзання стає дуже великим. Звідси, у малих колесах ніжка зношується сильніше ніж у великих. Зазначимо, що значення коефіцієнтів
|
||||
|
Последнее изменение этой страницы: 2016-06-22; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.74.47 (0.007 с.) |

 . (5)
. (5) ,
, ,
, – ширина зубчастих коліс; Е – зведений модуль пружності їхніх матеріалів; r - зведений радіус кривини евольвентних профілів у точці контакту; J – коефіцієнт питомого тиску.
– ширина зубчастих коліс; Е – зведений модуль пружності їхніх матеріалів; r - зведений радіус кривини евольвентних профілів у точці контакту; J – коефіцієнт питомого тиску. .
.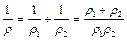 та що згідно з властивостями евольвентних профілів радіус кривини r - відстань від точки контакту К до основного кола (
та що згідно з властивостями евольвентних профілів радіус кривини r - відстань від точки контакту К до основного кола ( ,
,  ), розрахункова формула для коефіцієнта J має вигляд
), розрахункова формула для коефіцієнта J має вигляд . (6)
. (6) .
. енергії у зачепленні і стійкість зубців проти спрацьовування та заїдання.
енергії у зачепленні і стійкість зубців проти спрацьовування та заїдання. у відносному русі профілів
у відносному русі профілів ,
, - змінна відстань від точки дотикання профілів зубців до полюса зачеплення.
- змінна відстань від точки дотикання профілів зубців до полюса зачеплення.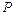 вона дорівнює нулю, а при переході через полюс міняє свій знак. Чим далі розміщена т. К від полюса
вона дорівнює нулю, а при переході через полюс міняє свій знак. Чим далі розміщена т. К від полюса  (див. рис. 9.3).
(див. рис. 9.3).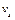 профілів до дотичних складових швидкостей точок дотику
профілів до дотичних складових швидкостей точок дотику  спряжених профілів
спряжених профілів ,
,  .
.
 та
та 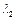 мають такий вигляд
мають такий вигляд ;
;  , (7)
, (7) – алгебраїчне значення відстані від полюса до точки контакту пари зубців (з урахуванням знаку);
– алгебраїчне значення відстані від полюса до точки контакту пари зубців (з урахуванням знаку);  - абсолютні значення довжини відрізків
- абсолютні значення довжини відрізків  .
.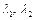 залежить від коефіцієнтів зміщення. Із зростанням коефіцієнтів
залежить від коефіцієнтів зміщення. Із зростанням коефіцієнтів  коефіцієнти ковзання збільшуються.
коефіцієнти ковзання збільшуються.


