
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кутовим прискоренням називають фізичну величину, що визначає зміну кутової швидкості в часі.Содержание книги
Поиск на нашем сайте
Кутове прискорення можна знайти, якщо продиференціювати за часом кутову швидкість:
Якщо Наведені формули визначають Зауважимо, що Лінійними далі будемо називати швидкості і прискорення точок тіла на відміну від кутових Розглянемо розподіл лінійних швидкостей у тілі, що обертається навколо нерухомої осі. Скористаємося натуральним способом визначення руху точки і розглянемо рух довільної точки
де
або
Напрям вектора швидкості Отже, лінійні швидкості залежно від радіуса обертання розподіляються за лінійним законом (рис. 2.15). Щоб знайти розподіл лінійних прискорень, скористаємось формулами (2.34) і (2.44). Дістанемо
Модуль повного прискорення знайдемо за формулою
Кут
Оскільки
2.2.4. Вектори кутової швидкості і кутового прискорення. Формула Ейлера
Узагальнимо поняття про кутову швидкість тіла, що обертається навколо осі. Виберемо початок прямокутної декартової системи координат на осі обертання (рис. 2.17) і вважатимемо, що вона незмінно зв’язана з тілом і обертається разом з ним. Орт Визначимо швидкість довільної точки
Координати
Визначимо похідні Вектор
і напрямлений цей вектор по дотичній до кола радіуса Згідно з цим дістанемо
Якщо кутова швидкість Аналогічно знайдемо
Згідно з (2.49) швидкість точки
З курсу векторної алгебри відомі співвідношення
Підставивши (2.51) в (2.50), дістанемо
Винесемо за дужки
Вектор
Згідно з (2.53), вектор Тоді (2.52) набуває вигляду
Цю формулу називають формулою Ейлера. У проекціях на декартові осі координат
Поняття вектора кутової швидкості і формули Ейлера дістали, розглядаючи найпростіший обертальний рух тіла – обертання навколо нерухомої осі. Здобуті висновки буде поширено на більш загальні випадки руху твердого тіла. Розглянемо вектор кутового прискорення. Кутове прискорення – це вектор, що характеризує зміну вектора кутової швидкості в часі. Тому
Очевидно, вектор при обертанні тіла навколо нерухомої осі вектор кутового прискорення Якщо обертання тіла прискорене, то напрями векторів
2.2.5. Рух вільного твердого тіла. Розподіл швидкостей і прискорень точок у вільному твердому тілі
Основна ознака абсолютно твердого тіла – незмінність відстаней між довільними точками такого тіла. Звідси випливає властивість збереження кута між двома довільними прямими, проведеними в абсолютно твердому тілі. Як буде показано далі, цих властивостей досить для визначення основного закону розподілу лінійних швидкостей і прискорень у вільному твердому тілі. Розглянемо точку
З тілом А незмінно зв’язана система координат
На підставі (2.56) знайдемо швидкість точки М:
Рисунок 2.19 Необхідно знайти похідні
Ці рівняння означають збереження довжин ортів Диференціюючи рівності (2.58) за часом, дістанемо
Отримані рівності – умови ортогональності векторів відповідно
Тут З (2.59) після диференціювання їх за часом дістанемо
Підставляючи (2.60) в (2.61), маємо
звідки на підставі властивостей змішаного добутку векторів
або
Вектор Аналогічно Отже,
а рівності (2.60) мають вигляд:
Рівність (2.57), що визначає швидкість точки М на підставі (2.63), набуває вигляду
або
У виразі (2.64) фізичний зміст вектора Наприклад, якщо вісь обертання нерухома і полюс знаходиться на цій осі, то Рівність (2.64) визначає закон розподілу швидкостей у вільному твердому тілі.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 515; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.72.173 (0.007 с.) |

 [рад/с2]. (2.43)
[рад/с2]. (2.43) і
і  одного знаку, то кутова швидкість зростає (обертання прискорене).
одного знаку, то кутова швидкість зростає (обертання прискорене). і
і  характеризують рух усього тіла.
характеризують рух усього тіла. тіла. Якщо початкове положення точки
тіла. Якщо початкове положення точки  відповідає початковому значенню кута повороту
відповідає початковому значенню кута повороту  , то з
, то з  ,
, – відстань точки
– відстань точки  за часом:
за часом: ,
, . (2.44)
. (2.44) перпендикулярний до радіуса обертання
перпендикулярний до радіуса обертання  .
.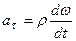 ;
;  ; (2.45)
; (2.45) ;
;  . (2.46)
. (2.46) ;
;  . (2.47)
. (2.47) між вектором повного прискорення і радіусом обертання (рис. 2.16):
між вектором повного прискорення і радіусом обертання (рис. 2.16): . (2.48)
. (2.48)

 лежить на нерухомій осі
лежить на нерухомій осі 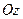 , орти
, орти 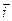 і
і  , зберігаючи модуль, змінюють напрям.
, зберігаючи модуль, змінюють напрям. розкладемо по ортах системи координат:
розкладемо по ортах системи координат: .
.

 точки М і орт
точки М і орт  . (2.49)
. (2.49) і
і  .
. , що викреслює годограф вектора
, що викреслює годограф вектора 
 , тобто перпендикулярно до осі
, тобто перпендикулярно до осі  і паралельно осі
і паралельно осі  (рис. 2.18).
(рис. 2.18). .
. збігається з ортом
збігається з ортом  .
. . (2.50)
. (2.50) ;
;  ;
; 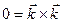 . (2.51)
. (2.51) .
.
 . (2.52)
. (2.52) називають вектором кутової швидкості:
називають вектором кутової швидкості: . (2.53)
. (2.53)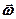 напрямлений уздовж осі обертання в той бік, звідки обертальний рух видно проти ходу годинникової стрілки. Точка прикладання
напрямлений уздовж осі обертання в той бік, звідки обертальний рух видно проти ходу годинникової стрілки. Точка прикладання  . (2.54)
. (2.54)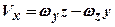 ;
;  ;
; 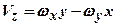 .
. . (2.55)
. (2.55) напрямлений по дотичній до годографа вектора кутової швидкості. У розглянутому випадку годографом вектора
напрямлений по дотичній до годографа вектора кутової швидкості. У розглянутому випадку годографом вектора  є пряма, що збігається з віссю обертання. Отже,
є пряма, що збігається з віссю обертання. Отже, напрямлений вздовж осі обертання.
напрямлений вздовж осі обертання. вільного твердого тіла
вільного твердого тіла 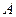 довільної форми (рис. 2.19).
довільної форми (рис. 2.19). . Точка
. Точка  нерухома. Точку О назвемо полюсом. З рис. 2.19 видно, що радіус-вектор
нерухома. Точку О назвемо полюсом. З рис. 2.19 видно, що радіус-вектор  . (2.56)
. (2.56) . (2.57)
. (2.57)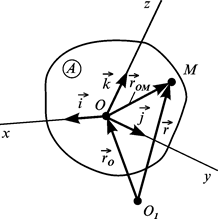
 . Для цього скористаємося згаданими властивостями абсолютно твердого тіла. Розглянемо дві системи рівностей
. Для цього скористаємося згаданими властивостями абсолютно твердого тіла. Розглянемо дві системи рівностей ; (2.58)
; (2.58)
 . (2.59)
. (2.59) і кутів між ними.
і кутів між ними.
 . (2.60)
. (2.60) – довільні вектори.
– довільні вектори. . (2.61)
. (2.61) ,
, ,
, . (2.62)
. (2.62) . У загальному випадку руху вільного твердого тіла вектор
. У загальному випадку руху вільного твердого тіла вектор  не буде перпендикулярним до орту
не буде перпендикулярним до орту  або
або  .
. .
. ,
, . (2.63)
. (2.63) ,
, . (2.64)
. (2.64) і
і  , де
, де 


