
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометричне місце миттєвих осей обертання, віднесене до рухомої системи координат, незмінно зв’язаної з тілом, називають рухомим аксоїдом.Содержание книги
Поиск на нашем сайте
Вершини аксоїдів збігаються з нерухомою точкою і в кожний момент часу мають спільну твірну, яка в цей момент є миттєвою віссю обертання. Теорема Пуансо. При русі тіла навколо нерухомої точки рухомий аксоїд котиться по нерухомому без ковзання. Коченням без ковзання називають рух двох тіл, що задовольняє двом умовам: Умова 1. Геометричні поверхні тіл дотикаються в спільних точках; Умова 2. Швидкості спільних точок обох тіл відносно нерухомої системи координат однакові. Справді, спільні точки поверхонь аксоїдів лежать на миттєвій осі обертання. Отже, швидкості точок рухомого аксоїда, що збігаються з точками нерухомого аксоїда, дорівнюють нулеві. Щоб переконатися у виконанні першої умови, треба скористатися властивостями кривих, що дотикаються [ 7 ]. Застосування теореми Пуансо можна розглядати як один із засобів синтезу механізмів, завдання якого полягає в побудові механізму, що здійснює заданий рух. Щоб здійснити рух тіла навколо нерухомої точки, слід побудувати рухомий і нерухомий аксоїди, з’єднати їх уздовж спільної твірної і котити без ковзання рухомий аксоїд по нерухомому. Теорема Ейлера. Кути Ейлера. Рівняння руху твердого тіла з нерухомою точкою
Визначимо закон руху тіла навколо нерухомої точки. Зв’яжемо незмінно з тілом систему координат
Рисунок 2.43
Припустимо, що в початковий момент часу осі цих систем координат збігаються. Положення системи Теорема Ейлера. Довільне переміщення тіла навколо нерухомої точки можна здійснити трьома послідовними поворотами тіла навколо трьох особливим способом вибраних осей, що проходять через нерухому точку. Перший поворот на кут Кути поворотів Кожному моменту часу відповідають певні значення кутів Ейлера. Отже, кути Ейлера є функціями часу:
Ці рівняння називають рівняннями руху тіла навколо нерухомої точки. З доведеної леми (підрозд. 2.2.11) можна зробити логічний висновок: миттєва кутова швидкість
Модуль вектора Розкладемо вектор
Знайдемо проекції кутової швидкості Тоді матимемо
Зауважимо, що
Далі знаходимо
Підставляємо ці вирази у (2.87), тоді маємо
Так само можна знайти проекції
Знаходимо:
На цій підставі маємо
Формули (2.88) і (2.89) називають кінематичними формулами Ейлера. Якщо проекції
Вектор кутового прискорення Зауважимо, що на практиці часто зустрічається випадок руху тіла навколо нерухомої точки, коли кутові швидкості прецесії
Розподіл швидкостей і прискорень
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 288; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.113.44 (0.01 с.) |


 з початком у тій самій точці О.
з початком у тій самій точці О.
 здійснюємо навколо осі
здійснюємо навколо осі 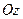 . Вісь
. Вісь  займає проміжне положення
займає проміжне положення  . Другий поворот на кут
. Другий поворот на кут  здійснюємо навколо осі
здійснюємо навколо осі  суміститься із своїм кінцевим положенням, а осі
суміститься із своїм кінцевим положенням, а осі  займуть проміжні положення, а вісь
займуть проміжні положення, а вісь  – кінцеве. Третій поворот робимо навколо цієї осі
– кінцеве. Третій поворот робимо навколо цієї осі  . Рухома система координат
. Рухома система координат 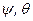 і
і  . (2.85)
. (2.85)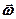 тіла, що рухається навколо нерухомої точки, дорівнює векторній сумі кутових швидкостей прецесії
тіла, що рухається навколо нерухомої точки, дорівнює векторній сумі кутових швидкостей прецесії  нутації
нутації  і власного обертання
і власного обертання  :
: .
. можна знайти, якщо визначити його проекції на осі ортогональної (рухомої або нерухомої) системи координат. Проекції вектора
можна знайти, якщо визначити його проекції на осі ортогональної (рухомої або нерухомої) системи координат. Проекції вектора  осей
осей 
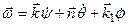 . (2.86)
. (2.86) .
. (2.87)
(2.87) .
.
 ;
; ;
; .
. (2.88)
(2.88) . Дістаємо
. Дістаємо

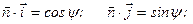
 .
.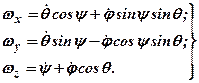 (2.89)
(2.89) .
. напрямлений по дотичній до годографа вектора кутової швидкості
напрямлений по дотичній до годографа вектора кутової швидкості  і власного обертання
і власного обертання  – сталі, і, як наслідок, кут нутації
– сталі, і, як наслідок, кут нутації 


