
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Точок тіла з нерухомою точкоюСодержание книги
Поиск на нашем сайте
За формулою (2.83) визначають швидкість довільної точки
Початок нерухомої системи координат збігається з нерухомою точкою. Проектуючи ліву і праву частини рівності (2.90) на осі
Прискорення довільної точки М визначається за (2.84)
Цей вираз можна переписати інакше:
Перший доданок у (2.92) називають обертальним прискоренням, другий — доосьовим
Напрями прискорень вектор лежить у тій площині, в якій лежать вектори Модулі складових обертального і доосьового прискорень точки можна визначити за формулами:
Рисунок 2.44
Приклад 2.7. Конус з висотою 4 м і радіусом основи Визначити кутову швидкість
Рисунок 2.45 Розв’язання. На підставі теореми Пуансо твердимо, що бічна поверхня конуса є рухомим аксоїдом, а площина
Швидкість точки С спрямована протилежно осі Величину
Отже,
Кут утворений осями: прецесії
Як видно з рис. 2.45, трикутник, утворений векторами
Кутове прискорення
Вектор
Швидкість точки
Швидкість точки
Оскільки Прискорення точок А і В знайдемо за формулами:
Обчислимо кожний доданок і визначимо напрям. Напрями доосьових прискорень знаходимо за правилом векторного добутку:
Як було зазначено, Доосьове прискорення Величина Обертальне прискорення Величина Оскільки Напрями Отже, Величину прискорення точки
Складний рух твердого тіла Найпростішими рухами твердого тіла є, як було показано вище, поступальний і обертальний рух навколо нерухомої осі. Але абсолютно тверде тіло може одночасно брати участь у двох або кількох рухах: поступальних, обертальних навколо паралельних осей, чи осей, що перетинаються, поступальному і обертальному, тощо. Основною задачею кінематики складного руху абсолютно твердого тіла є встановлення залежностей між основними кінематичними характеристиками рухів, що додаються, і визначення характеру результуючого руху твердого тіла. Поняття про абсолютний, відносний і переносний рухи, розглянуті при вивченні складного руху матеріальної точки, розповсюдимо на випадок додавання рухів твердого тіла. Обмежимось випадком додавання двох рухів, один із яких вважатимемо відносним, другий – переносним. Визначимо абсолютну швидкість довільної точки тіла, що бере участь у двох рухах, і за отриманими результатами зробимо висновок про характер результуючого руху.
|
|||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 261; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.233.4 (0.007 с.) |

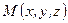 тіла:
тіла: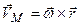 . (2.90)
. (2.90)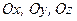 , визначимо проекції швидкості точки М на ці осі:
, визначимо проекції швидкості точки М на ці осі: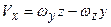 ;
;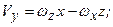 (2.91)
(2.91)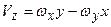 .
.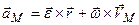 .
. . (2.92)
. (2.92)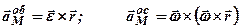 . (2.93)
. (2.93)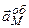 і
і 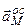 повністю визначаються за (2.93). З виразу доосьового прискорення видно, що
повністю визначаються за (2.93). З виразу доосьового прискорення видно, що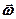 і
і 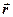 , і напрямлений по перпендикуляру до вектора
, і напрямлений по перпендикуляру до вектора 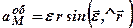 ; (2.94)
; (2.94)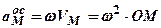 . (2.95)
. (2.95)
 , кутове прискорення
, кутове прискорення  конуса, а також швидкість і прискорення його точок
конуса, а також швидкість і прискорення його точок 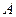 і
і 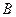 , якщо швидкість центра основи конуса
, якщо швидкість центра основи конуса 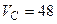 см/с = const.
см/с = const.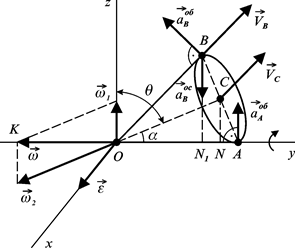
 – нерухомим аксоїдом. Миттєва вісь обертання – твірна конуса
– нерухомим аксоїдом. Миттєва вісь обертання – твірна конуса 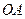 . Вектор
. Вектор 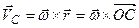 ,
, 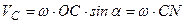 .
. .
.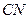 знаходимо з прямокутного трикутника
знаходимо з прямокутного трикутника 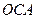 :
: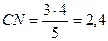 см.
см. рад/с.
рад/с.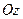 і власного обертання
і власного обертання 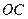 , є кутом нутації
, є кутом нутації  . Оскільки він залишається незмінним, має місце регулярна прецесія. Отже, кутова швидкість
. Оскільки він залишається незмінним, має місце регулярна прецесія. Отже, кутова швидкість  і кутової швидкості власного обертання
і кутової швидкості власного обертання 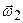 :
: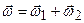 .
. , сторони якого відомі:
, сторони якого відомі: 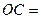 = 4 см,
= 4 см, 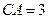 см,
см,  см. Елементарні геометричні міркування дають змогу знайти
см. Елементарні геометричні міркування дають змогу знайти рад/с;
рад/с; 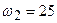 рад/с.
рад/с.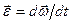 можна розглядати як швидкість точки
можна розглядати як швидкість точки 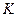 , що викреслює годограф вектора кутової швидкості
, що викреслює годограф вектора кутової швидкості  .
.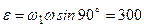 рад/с2.
рад/с2. навколо миттєвої осі
навколо миттєвої осі  .
. , то
, то  см/с. Швидкість точки
см/с. Швидкість точки 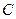 .
.
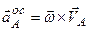 ;
;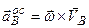 .
. , тому
, тому 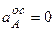 .
.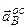 точки
точки 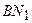 обертання точки
обертання точки 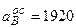 см/с2.
см/с2.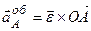 ;
; 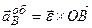 .
.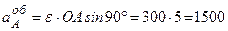 см/с2.
см/с2.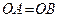 , то
, то 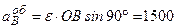 см/с2.
см/с2. і
і 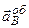 знаходимо за правилом векторного добутку. Ці прискорення знаходяться в площині трикутника
знаходимо за правилом векторного добутку. Ці прискорення знаходяться в площині трикутника 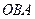 і перпендикулярні
і перпендикулярні 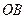 відповідно.
відповідно.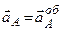 ,
, 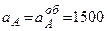 см/с2.
см/с2.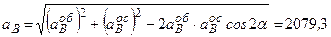 см/с2.
см/с2.


