
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Плоскопаралельним називають такий рух твердого тіла, під час якого всі точки тіла рухаються паралельно певній нерухомій площині, яку називають основною.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Багато механізмів, які зустрічаються на практиці, належать до так званих плоских механізмів. Тому вивчення плоскопаралельного руху тіла має істотне практичне значення. Плоскопаралельний рух можна розглядати як окремий випадок руху вільного твердого тіла. У цьому випадку миттєва вісь обертання перпендикулярна до основної площини. Покажемо, що з означення плоскопаралельного руху випливає можливість звести задачу вивчення руху тіла в просторі до задачі вивчення руху плоскої фігури в площині. Тіло перебуває в плоскопаралельному русі (рис. 2.23), площина
Рисунок 2.23
Складемо рівняння руху плоскої фігури. Виберемо дві системи координат: нерухому
Структура цих рівнянь показує, що рух плоскої фігури можна розглядати як складний: поступальний разом з полюсом О – рівняння (2.69), (2.70) і обертальний навколо полюса О рівняння 2.71. Якщоперенести полюс із точки О в іншу точку, рівняння (2.71) не зміниться, зміняться лише рівняння(2.69) і (2.70). З цих міркувань можна зробити висновок: при плоскопаралеьному русі твердого тіла характеристики обертального руху (кут повороту
Рисунок 2.24 Розглядаючи плоскопаралельний рух як окремий випадок руху вільного твердого тіла, можна зобразити Рівняння руху довільної точки М тіла знайдемо, скориставшись формулами перетворення координат:
2.2.7. Розподіл швидкостей точок тіла при Розглянемо плоскопаралельний рух тіла як окремий випадок руху вільного твердого тіла, скориставшись співвідношенням (2.64). Позначимо другий доданок у правій частині цього виразу
де
Цей вираз є законом розподілу швидкостей у тілі при плоскопаралельному русі.
Рисунок 2.25 Зауважимо, що вектор Таким чином, Швидкість довільної точки плоскої фігури дорівнює векторній сумі швидкостей полюса і обертального руху точки навколо полюса. Із (2.74) можна зробити висновок, що в кожний момент часу існує точка, швидкість якої дорівнює нулеві, тобто Якщо полюс вибрати в миттєвому центрі швидкостей, то на підставі (2.74)
Отже, Швидкості точок плоскої фігури можна розглядати як швидкості її обертального руху навколо миттєвого центра швидкостей. Тому миттєвий центр швидкостей називають ще миттєвим центром обертання. Розглянемо побудову миттєвого центра швидкостей. Для цього існує кілька способів. Спосіб 1. Якщо відома швидкість
Рисунок 2.26 Звідси
Миттєвий центр швидкостей лежить на прямій РО, перпендикулярній до вектора Спосіб 2. Нехай відомі прямі, уздовж яких напрямлені швидкості двох точок А і В плоскої фігури (рис. 2.27), і відома швидкість точки
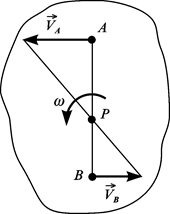
Рисунок 2.27 Спосіб 3. Існує ще кілька окремих випадків визначення миттєвого центра швидкостей: а) швидкості двох точок тіла паралельні, неоднакові і мають один напрям (рис. 2.28, а); б) швидкості двох точок тіла паралельні, неоднакові і мають різні напрями (рис. 2.28, б);
в) швидкості двох точок тіла паралельні, однакові, напрямлені в один бік (рис. 2.29). У цьому разі миттєва кутова швидкість г) у деяких випадках можна знайти положення миттєвого центра швидкостей з умови кочення без ковзання: миттєвий центр знаходиться в точці дотику тіла з нерухомою поверхнею (рис. 2.30). Зауважимо, що під час руху тіла положення миттєвого центра швидкостей змінюється. Геометричне місце миттєвих центрів швидкостей, віднесене до рухомої або нерухомої системи координат, називають відповідно рухомою або нерухомою центроїдою.
З цією геометричною інтерпретацією плоскопаралельного руху пов’язана теорема Пуансо:
|
|||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 503; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.37.211 (0.006 с.) |

 – основна. Зробимо перетин
– основна. Зробимо перетин  тіла площиною, паралельною основній, і розглянемо рух прямої АВ, перпендикулярної до площини
тіла площиною, паралельною основній, і розглянемо рух прямої АВ, перпендикулярної до площини  . За означенням плоскопаралельного руху рух прямої АВ – поступальний. Отже, рух довільної точки А цієї прямої визначає цей поступальний рух. Якщо повторити ці міркування для будь-якої точки плоскої фігури
. За означенням плоскопаралельного руху рух прямої АВ – поступальний. Отже, рух довільної точки А цієї прямої визначає цей поступальний рух. Якщо повторити ці міркування для будь-якої точки плоскої фігури 
 . Положення системи координат
. Положення системи координат  . Положення осей
. Положення осей  і
і  визначається кутом
визначається кутом  . Отже, три параметри
. Отже, три параметри  повністю визначають положення плоскої фігури. Якщо кожному моменту часу
повністю визначають положення плоскої фігури. Якщо кожному моменту часу 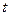 поставити у відповідність значення величин
поставити у відповідність значення величин  , то дістанемо рівняння, які є законом руху плоскої фігури:
, то дістанемо рівняння, які є законом руху плоскої фігури: ; (2.69)
; (2.69) ; (2.70)
; (2.70) . (2.71)
. (2.71) , кутова швидкість
, кутова швидкість 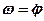 , кутове прискорення
, кутове прискорення 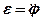 ) не залежать від вибору полюса.
) не залежать від вибору полюса.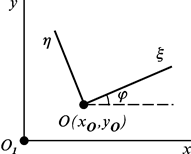
 і
і  у вигляді векторів, перпендикулярних до площини руху тіла.
у вигляді векторів, перпендикулярних до площини руху тіла. ;
; . (2.72)
. (2.72) , (2.73)
, (2.73)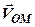 — швидкість обертального руху точки М плоскої фігури навколо полюса О. Тоді маємо (рис. 2.25)
— швидкість обертального руху точки М плоскої фігури навколо полюса О. Тоді маємо (рис. 2.25)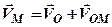 . (2.74)
. (2.74)
 перпендикулярний до вектора
перпендикулярний до вектора  .
. . Цю точку Р, швидкість якої дорівнює нулеві, називають миттєвим центром швидкостей.
. Цю точку Р, швидкість якої дорівнює нулеві, називають миттєвим центром швидкостей. .
.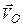 певної точки О фігури і миттєва кутова швидкість
певної точки О фігури і миттєва кутова швидкість  , то миттєвий центр Р швидкостей (рис. 2.26) знайдемо на прямій ОР, перпендикулярній до
, то миттєвий центр Р швидкостей (рис. 2.26) знайдемо на прямій ОР, перпендикулярній до  .
.  ;
; і
і  .
.
 .
. на відстані
на відстані  . Розглянемо швидкості
. Розглянемо швидкості  як швидкості обертального руху навколо миттєвого центра обертання Р. Ці швидкості мають бути перпендикулярні до радіусів обертання РА і РВ. Отже, проводимо
як швидкості обертального руху навколо миттєвого центра обертання Р. Ці швидкості мають бути перпендикулярні до радіусів обертання РА і РВ. Отже, проводимо  і
і  . У точці їх перетину знаходиться миттєвий центр Р швидкостей. Знаючи швидкість
. У точці їх перетину знаходиться миттєвий центр Р швидкостей. Знаючи швидкість  точки А, знаходимо напрям і величину миттєвої кутової швидкості
точки А, знаходимо напрям і величину миттєвої кутової швидкості 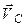 знаходимо згідно з напрямом обертання плоскої фігури навколо Р – миттєвого центра швидкостей. Модулі векторів швидкостей обчислюємо з пропорції
знаходимо згідно з напрямом обертання плоскої фігури навколо Р – миттєвого центра швидкостей. Модулі векторів швидкостей обчислюємо з пропорції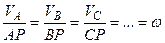 . (2.75)
. (2.75)
 а
а
 б
б
 і тіло в цей момент часу виконує миттєвий поступальний рух;
і тіло в цей момент часу виконує миттєвий поступальний рух;




