Паралельність прямої та площини. Паралельність площин.

1. Ознакою паралельності площини і пря­мої є паралельність прямої будь-якій прямій цієї площини.

2. Ознакою паралельності проекційної пло­щини і прямої є паралельність сліду — проекції площини відповідній проекції заданої прямої.

3. Дві площини, задані слідами, взаємно паралельні, якщо їх однойменні сліди пара­лельні між собою.

4. Площини, задані перетинними (парале­льними) прямими, паралельні, якщо перетинні (паралельні) прямі однієї площини відповід­но паралельні прямим другої площини.

5. Горизонталі і фронталі двох паралель­них площин паралельні між собою. Ця особ­ливість паралельних площин використовуєть­ся для з'ясування паралельності двох пло­щин, якщо одна з площин або обидві задані не слідами.

Перпендикулярність прямої і площини

 

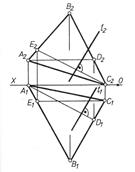
1. Пряма і площина взаємно перпендику­лярні, якщо горизонтальна проекція прямої перпендикулярна до горизонтальної проек­ції горизонталі, а фронтальна — до фронта­льної проекції фронталі площини.

На рис. 4.1 пряма l перпендикулярна до площини трикутникаАВС, оскільки l₁ A₁D₁, а l₁ C₂E₂ (АD — горизонталь, СЕ — фронталь площини).

Рис. 4.1

2. Якщо пряма перпендикулярна до пло­щини, заданої слідами, то проекції цієї пря­мої перпендикулярні до відповідних слідів площини.

3. Відстань від точки до площини визнача­ють довжиною перпендикуляра, проведеного з точки на площину. Алгоритм цього визна­чення такий:

а) проведення перпендикуляра із заданої точки на площину;

б) знаходження точки перетину перпенди­куляра з площиною;

в) визначення справжньої довжини знай­деного перпендикуляра.

 

 

Взаємно перпендикулярні прямі

Дві прямі взаємно перпендикулярні, якщо одна з них лежить у площині, перпендикуляр­ній до другої прямої.

Щоб провести через точку А пряму Р, пер­пендикулярну до заданої прямої l, через задану точку проводимо площину О, перпендикулярну до прямої l (цю площину вигідно задавати горизонталлю і фронталлю). Далі знаходимо точку перетину К пря­мої l з площиною Q і проводимо через неї та задану точку А шуканий перпендикуляр.

Взаємно перпендикулярні прямі

 

1. Щоб одна площина була перпендикуляр­на до іншої, досить, щоб одна з них проходила через перпендикуляр до іншої.

2. Побудову площини Q, перпендикулярної до площини Р, можна виконати двома спосо­бами: а) площину Q проводимо через пряму, перпендикулярну до площини Р; б) площину Q проводимо перпендикулярно до прямої, що лежить у площині Р. Щоб одержати єдиний розв'язок, потрібні додаткові умови.

3. Якщо горизонтальні сліди двох го­ризонтально-проекційних площин взаємно перпендикулярні, то й площини взаємно пер­пендикулярні. Якщо фронтальні сліди двох фронтально-проекційних площин взаємно перпендикулярні, то й площини взаємно пер­пендикулярні.

4. Перпендикулярність горизонтальних слідів площини довільного положення і го­ризонтально-проекційної площини відповідає взаємній перпендикулярності цих площин. Перпендикулярність фронтальних слідів площини довільного положення і фронталь­но-проекційної площини відповідає взаємній перпендикулярності цих площин.

5. Якщо однойменні сліди двох площин до­вільного положення взаємно перпендикулярні, то ці площини не перпендикулярні між собою.

 

Завдання 8. Перпендикулярність прямої і площини

 

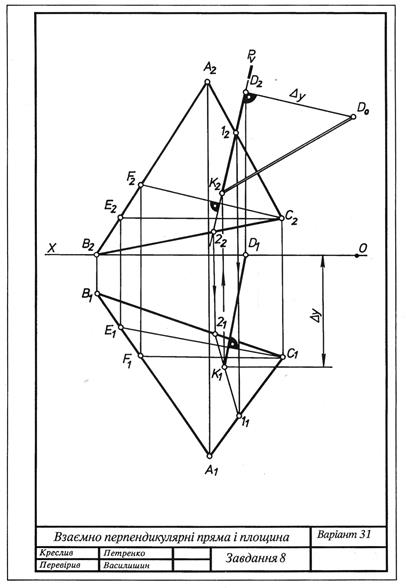
Визначити справжню величину відстані від точки О до площини, заданої трикутником АВС (завдання розв'язати без перетворення ортогональних проекцій).

Дані до завдання взяти з табл.4.

Приклад виконання подано на рис.4.2.

 

 

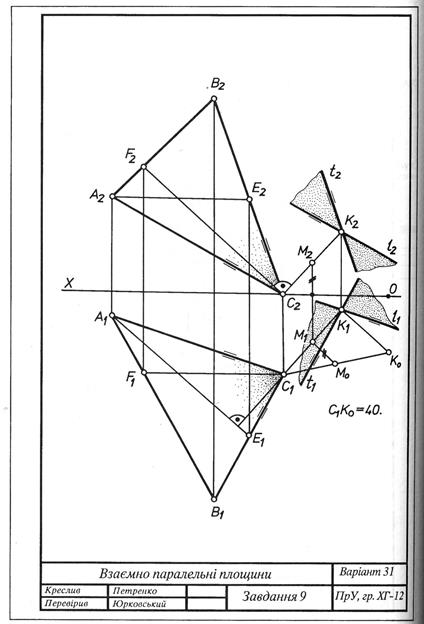
Завдання 9 Паралельність площин

Побудувати площину на відстані 40 мм паралельно площині, заданій трикутником АВС (задачу розв'язати без перетворення ортогональних проекцій).

Дані до задачі взяти з табл. 4.

Приклад виконання подано на рис. 4.3.

 

 

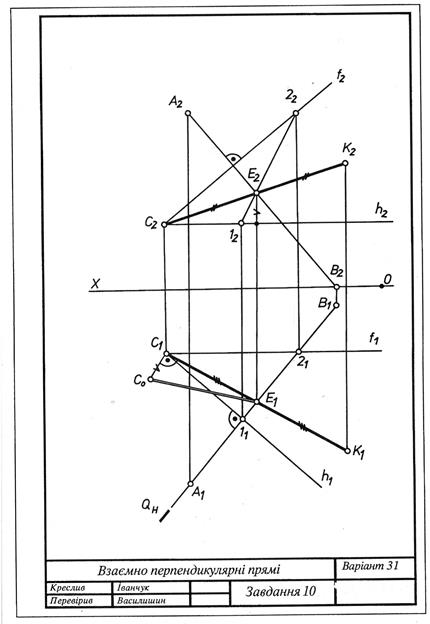
Завдання 10 Перпендикулярність прямих

Визначити справжню величину відстані від точки С до відрізка АВ і побудувати точку К, симетричну точці С відносно цього відрізка (задачу розв'язати без перетворення ортогона­льних проекцій).

Дані до задачі взяти з табл. 4

Приклад виконання подано на рис. 4.4

 

Табл. 4

 

Рис. 4.2

 

Рис. 4.3

Рис. 4.4