Належність прямої і точки площині

 

1. Пряма належить площині, якщо вона про­ходить: через дві точки, які належать цій пло­щині; через точку, яка належить цій площині і паралельна прямій, що розташована в цій площині або паралельній їй.

Якщо площина задана слідами, то пряма належить площині, якщо сліди прямої розта­шовані на однойменних слідах площини; пря­ма паралельна одному зі слідів цієї площини і має з іншим слідом спільну точку.

2. Точка належить площині, якщо вона на­лежить будь-якій прямій цієї площини.

 

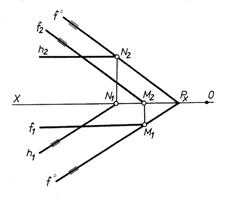
Прямі особливого положення в площині

Особливими прямими у площині є:

а) горизонталі — прямі, що лежать у пло­щині й паралельні горизонтальній площині проекцій;

б) фронталі — прямі, що лежать у площині й паралельні фронтальній площині проекцій;

в) профілі — прямі, що лежать у площині й паралельні профільній площині проекцій;

г) лінії найбільшого нахилу площини до площини проекцій — прямі, що лежать у площині й перпендикулярні до одного зі слідів площини.

У системі двох площин проекцій горизон­таль h (h₁,h₂) має лише один фронтальний слід N (N₁,N₂), який лежить на фронтальному сліді площини; її фронтальна проекція пара­лельна осі ОХ, а горизонтальна — горизонта­льному сліду площини (рис. 3.5). Фронталь f (f₁,f₂) має лише один горизонтальний слід M (M₁,M₂),, який лежить на горизонтальному сліді площини; її горизонтальна проекція па­ралельна осі ОХ, а фронтальна — фронталь­ному сліду площини (рис. 3.6).

 

Рис. 3.6

Перетин прямої з площиною

1. Для побудови точки перетину прямої з площиною загального положення необхідно (рис. 3.7, 3.8):

Рис. 3.7

Рис. 3.8

 

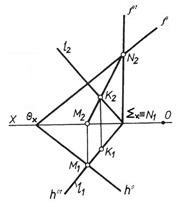
а) через задану пряму l (l₁,l₂) провести де­яку допоміжну площину ;

б) побудувати пряму МN (М₁N₁, М₂N₂) пе­ретину заданої площини з допоміжною;

в) визначити положення точки К (K₁, К₂) перетину прямих: заданої l і побудованої МN.

2. При побудові точки перетину прямої з площиною особливого положення побудова спрощується, оскільки одна з проекцій точки перетину міститься на прямій, у вигляді якої площина проекціюється на ту чи іншу пло­щину проекцій. На рис. 3.9 побудовано точку перетину
К (K₁, К₂) прямої l з горизон­тально-проекційною площиною ( AВС).

Рис. 3.9

 

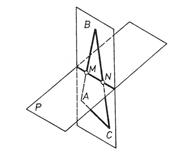
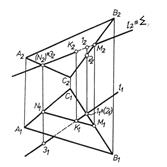
Перетин площин

Задачу на перетин двох площин довільно­го положення розв'язують двома способами:

1) побудувати точки перетину двох прямих однієї площини з іншою площиною, тобто двічі використати алгоритм пошуку точки перети­ну прямої з площиною. На рис. 3.10 площи­на, задана трикутником АВС, перетинається з площиною Р по прямій MN;

Рис. 3.10

2) використавши дві допоміжні січні пло­щини особливого положення, побудувати лі­нії їх перетину з заданими площинами. Дві відповідні точки перетину цих ліній визнача­ють шукану пряму перегину заданих площин. На рис. 3.11 задані площини Р і Q перетинаються по пря

мій MN. Використано допомі­жну площину Т, яка перетинається з площи­нами Р і Q відповідно по прямих а і b, та до­поміжну площину R, яка перетинається з пло­щинами Р і Q відповідно по прямих с і d.

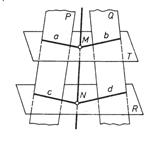
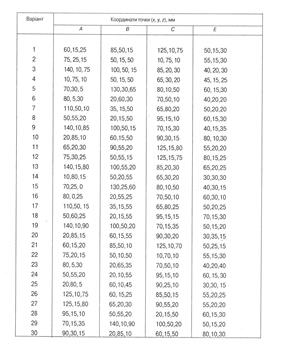
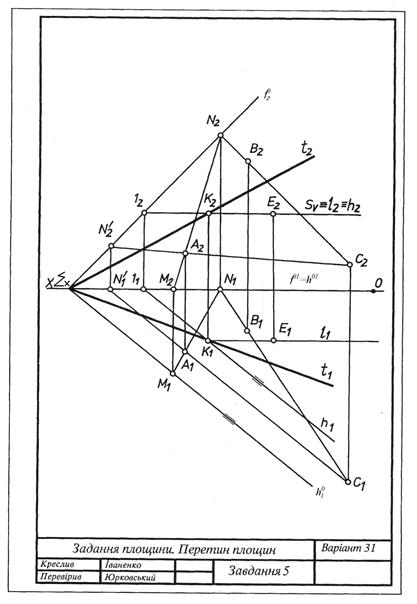
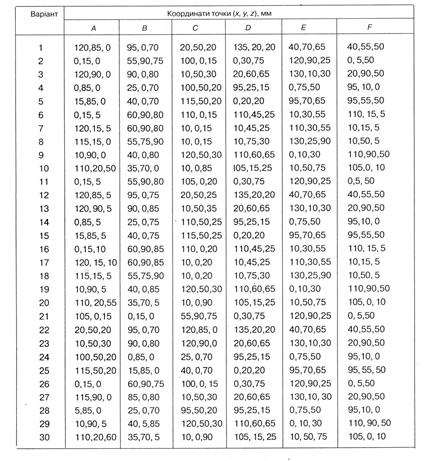
Рис. 3.11

Завдання 5. Задання та перетин площин

Побудувати сліди площини , заданої трьома точками А,В,С. Знайти лінію перетину цієї площини з осьовою площиною О, заданою точкою Е та f⁰¹=h⁰¹.

Дані до завдання взяти з табл. 3.1.

Приклад виконання подано на рис. 3.12.

Таблиця 3.1

Рис. 3.12

 

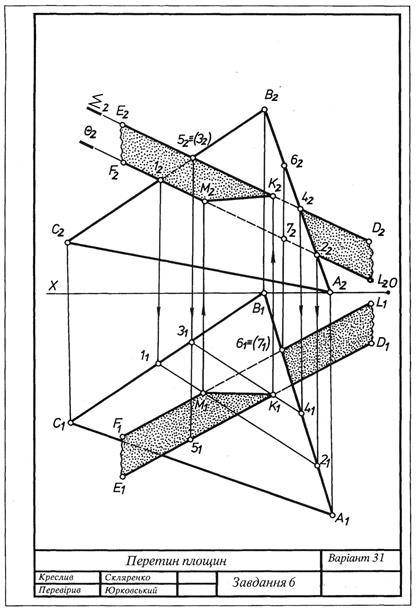
Завдання 6. Перетин площин загального положення

Побудувати лінію перетину площини, заданої трикутником АВС, з площиною, заданою паралельними прямими DE i FL. Визначити взаємну видимість площин.

Дані до завдання взяти з табл. 3.2. Точка L будується з умови паралельності прямих DE i FL.

Приклад виконання подано на рис. 3.13.

Таблиця 3.2

 

 

Рис. 3.13

 

Завдання 7. Перетин площин

 

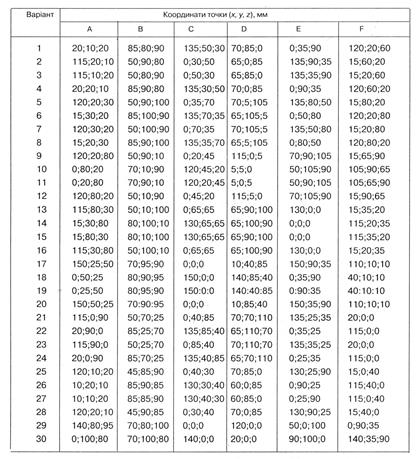
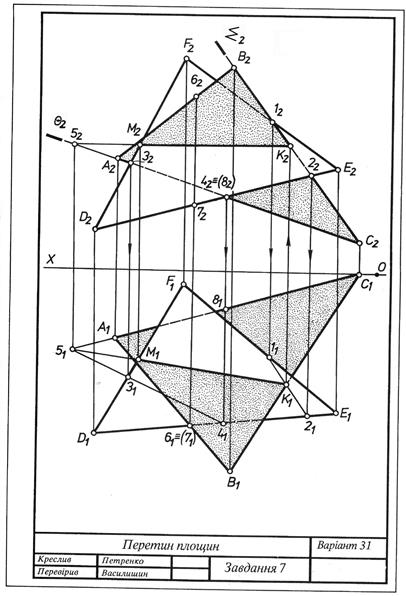
Побудувати лінію перетину площин, заданих трикутниками АВС I DEF. Визначити взаємну видимість площин.

Дані до завдання взяти з табл. 3.3.

Приклад виконання завдання подано на рис. 3.14.

 

Таблиця 3.3

 

 

Рис. 3.14

 

ТЕМА. ПЕРПЕНДИКУЛЯРНІСТЬ І ПАРАЛЕЛЬНІСТЬ ГЕОМЕТРИЧНИХ ЕЛЕМЕНТІВ

4.1 Мета і задачі вивчення теми:

Опанувати методи побудови креслень з перпендикулярними елементами (площина та пряма, площини між собою) та з паралельними елементами (площина та пряма, площини між собою).