Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Спосіб плоско паралельного переміщенняСодержание книги Поиск на нашем сайте
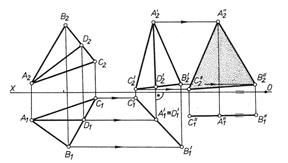
1. Плоскопаралельне переміщення є, по суті, способом обертання навколо осей — проекційних прямих без визначення на епюрі радіуса і осей обертання. Цей спосіб вигідно застосовувати, щоб уникнути накладання зображень фігур, які обертаються, на їх задані проекції. 2. На рис. 5.1 відрізок довільного положення АВ переведений у положення, перпендикулярне до площини проекцій П1. Спочатку переведено відрізок у лінію рівня — фронтальну пряму. Для цього пряма АВ переміщена навколо осі, перпендикулярної до горизонтальної площини проекцій. Далі плоскопаралельним переміщенням відносно осі, перпендикулярної до площини проекцій V, пряму АВ переведено в горизонтально-проекційне положення;
Рис. 5.1
Рис. 5.2 Завдання 11. Визначення справжньої величини трикутника
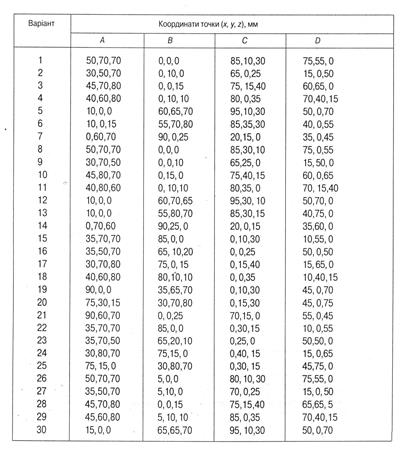
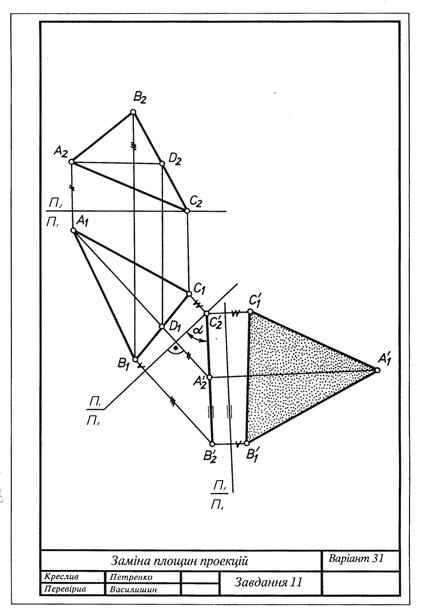
Способом заміни площин проекцій визначити справжню величину трикутника АВС та кут нахилу його до горизонтальної (варіанти 1-15) або фронтальної (варіанти 16-30) площини проекцій. Дані до завдання взяти з табл. 5. Приклад виконання подано на рис. 5.3.
Завдання 12. Визначення величини двогранного кута
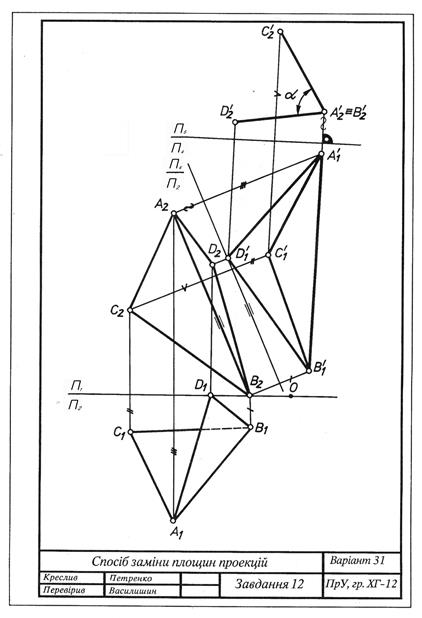
Способом заміни площин проекцій визначити величину двогранного кута, утвореного трикутниками АВС і АВD. Дані до завдання взяти з табл. 5. Приклад виконання подано на рис. 5.4.
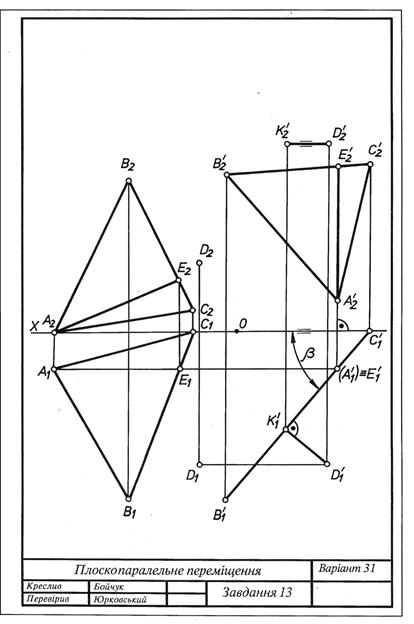
Завдання 13. Визначення відстані від точки до площини
Способом плоскопаралельного переміщення визначити відстань від точки D до площини, заданої трикутником АВС, та кут нахилу цієї площини до горизонтальної (варіанти 1-15) або фронтальної (варіанти 16-30) площини проекцій.
Дані до завдання взяти з табл. 5. Приклад виконання подано на рис. 5.5. Таблиця 5
Рис. 5.3
Рис. 5.4
Рис. 5.5 ТЕМА: ГРАНІ ПОВЕРХНІ ТА МНОГОГРАННИКИ Мета і задачі вивчення теми Опанувати знаннями утворення многогранник поверхонь, методами побудови креслень многогранників, та знаходити лінії перетину многогранників площинами і перетину многогранників між собою.
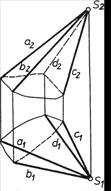
Грані поверхні 1. Многогранною називається поверхня, утворена частинами перетинних площин. 2. Декілька площин.(але не менше трьох), які перетинаються в якійсь точці, утворюють пірамідальну поверхню (рис. 6.1.). Ця точка (на рис. 4.1 — точка S) є вершиною, в якій перетинаються всі ребра піраміди (на рис. 4.1 —ребрао, a, b,с, d).
Рис. 6.1
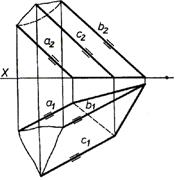
3. Призматична поверхня є окремим випадком пірамідальної з невласною вершиною. Всі ребра такої поверхні взаємно паралельні (рис.6.2).
Рис. 6.2 Многогранники 1. Многогранником називається тіло, обмежене многогранною поверхнею. 2. Сукупність усіх ребер і вершин много-гранника є його сіткою. 3. Якщо многогранник розташований з одного боку площини будь-якої його грані, то він називається випуклим. 4. Для отримання проекцій многогранника будують проекції його сітки (рис. 6.3).
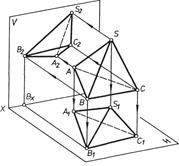
Рис. 6.3 5. Пірамідою називають многогранник, усі грані якого, крім однієї, мають спільну вершину; її називають вершиною піраміди. Звичайно піраміду задають на кресленні проекціями її основи і вершини (рис. 4.4), а зрізану
піраміду — проекціями обох основ (рис. 6.4). Якщо висота піраміди проходить через центр основи піраміди, то піраміда вважається прямою. Пряму піраміду називають правильною, якщо її основа — правильний многокутник.
Рис. 6.4 6. Призма — це многогранник, обмежений призматичною поверхнею і двома площинат ми, паралельними між собою, але не паралельними ребрам призми. Ці дві грані (рівні многокутники) називаються основами призми. Якщо основи не паралельні між собою, призма є зрізаною. 7. Многогранники, в яких усі ребра, грані, плоскі, двогранні та просторові кути рівні між собою, називаються правильними випуклими многогранниками (тілами Платона).
Існує п'ять таких тіл: а) тетраедр (чотиригранник), гранями якого є чотири рівносторонні трикутники; б) октаедр (восьмигранник), гранями якого є вісім рівносторонніх трикутників; в) ікосаедр (двадцятигранник), утворений з двадцяти рівносторонніх трикутників; г) гексаедр (шестигранник), або куб, гранями якого є шість квадратів; д) додекаедр (дванадцятигранник), утворений з дванадцяти правильних п'ятикутників. Навколо всіх правильних многогранників можна описати сферу.
|
||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 207; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.8.188 (0.008 с.) |

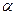 - кут між прямою АВ і горизонтальною площиною проекцій.
- кут між прямою АВ і горизонтальною площиною проекцій.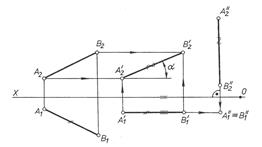

 3. На рис. 5.2 площину трикутника АВС загального положення переведено у фронтальну площину (площину рівня). Виконано послідовно два плоскопаралельні переміщення трикутника АВС: спочатку відносно осі, перпендикулярної до площини проекцій П2, потім відносно осі, перпендикулярної до площини проекцій П1. При першому плоскопаралельному переміщенні площину трикутника перетворено на горизонтально-проекційну, при цьому фронталь АD трикутника переведена в горизонтально-проекційне положення (А'1,D'2 Х). Другим плоскопаралельним переміщенням трикутник A'В'С' перетворено на трикутник A"В"С", при цьому фронтальна проекція А"2В"2С"2 визначає справжні розміри трикутника АВС.
3. На рис. 5.2 площину трикутника АВС загального положення переведено у фронтальну площину (площину рівня). Виконано послідовно два плоскопаралельні переміщення трикутника АВС: спочатку відносно осі, перпендикулярної до площини проекцій П2, потім відносно осі, перпендикулярної до площини проекцій П1. При першому плоскопаралельному переміщенні площину трикутника перетворено на горизонтально-проекційну, при цьому фронталь АD трикутника переведена в горизонтально-проекційне положення (А'1,D'2 Х). Другим плоскопаралельним переміщенням трикутник A'В'С' перетворено на трикутник A"В"С", при цьому фронтальна проекція А"2В"2С"2 визначає справжні розміри трикутника АВС.