Тема: проекції точки і прямої

МЕТОДИЧНІ ВКАЗІВКИ

до виконання контрольних робіт студентами

заочної форми навчання та індивідуальних завдань

студентами денної форми навчання з розділу нарисна геометрія дисципліни

„ІНЖЕНЕРНА ГРАФІКА”

(для студентів всіх спеціальностей)

 

 

СЄВЄРОДОНЕЦЬК 2005

УДК 22.151.3

 

Методичні вказівки до виконання контрольних робіт студентами заочної форми навчання та індивідуальних завдань студентами денної форми навчання з розділу нарисна геометрія дисципліни „Інженерна графіка” студентів всіх спеціальностей. Укл. М.І. Гуліда, Л.Г. Холіна.- Сєвєродонецьк: Вид-во СТІ 2005. 78 –с.

 

 

Приведені матеріали, необхідні для виконання контрольних робіт та індивідуальних завдань з дисципліни „Інженерна графіка”. Описані основні теоретичні положення з розділу „нарисна геометрія”, мета та задачі тем розділу. Складені варіанти завдань та наведені приклади виконання їх, дані контрольні питання по темам розділу.

 

 

Укладачі М.І. Гуліда

Л.Г. Холіна

 

Відповідальний за випуск О.Г. Архіпов

 

Рецензент О.О. Дорогін

 

 

Затверджено Вченою радою інституту.

Протокол №___ від „____” ___________ 2005р.

 

 

Голова Вченої ради,

К.т.н., доцент О.Г. Архіпов

ЗМІСТ

1. Область застосування..................................................... 4

2. Тема. Проекція точки і прямої....................................... 4

3. Тема. Проекціювання площин........................................ 19

4. Тема. Перпендикулярність і паралельність геометричних елементів.......................................................................... 30

5. Тема. Способи перетворення креслення....................... 38

6. Тема. Грані поверхні та многогранники....................... 45

7. Тема. Криві поверхні....................................................... 51

8. Тема. Перетин поверхонь............................................... 61

9. Порядок оформлення та захисту завдань, критерії
оцінки................................................................................ 74

10. Контрольні питання щодо захисту завдань.................. 74

Список літератури........................................................... 77

ОБЛАСТЬ ЗАСТОСУВАННЯ

 

Методичні вказівки призначені для виконання контрольних робіт студентами заочниками та індивідуальних завдань студентами денної форми навчання при вивченні дисципліни „Нарисна геометрія” або аналогічних розділів „Інженерної графіки”.

 

ТЕМА: ПРОЕКЦІЇ ТОЧКИ І ПРЯМОЇ

 

2.1. Мета і задачі вивчення теми:

 

Опанувати методи проеціювання точки і прямої лінії залежно від їх розташування в просторі, а також визначити основні параметри об’єктів проеціювання.

 

ТЕМА ПРОЕКЦЮВАННЯ ПЛОЩИН

 

3.1 Мета і задачі вивчення теми:

Опанувати методами зображення площин на кресленнях, та їх взаємодією з прямими лініями та другими площинами.

 

Способи задання площин на кресленні

1. Площина на епюрі може бути задана:

а) проекціями трьох точок, що не належать на одній прямій
(рис. 3.1);

б) проекціями прямої та точки, яка належить прямій (рис. 3.2)

в) проекціями паралельних прямих (рис. 3.3)

г) проекціями перетин них прямих (рис. 3.4)

д) проекціями плоскої фігури (рис. 3.5)

 

Рис. 3.1 Рис. 3.2 Рис. 3.3

 

 

 

Рис. 3.4 Рис. 3.5

 

Класифікація площин

1. Площину, не перпендикулярну і не пара­лельну до жодної з площин проекцій, назива­ють площиною довільного (загального) по­ложення (рис. 3.1-3.5).

Характерною ознакою довільної площини, заданої слідами, є те, що останні не перпен­дикулярні до площин проекцій.

 

2. Площину, перпендикулярну до одної або двох площин проекцій, називають особливою, перпендикулярну до одної площини проек­цій — проекційною; перпендикулярну до двох площин проекцій — площиною рівня.

У таблиці наведені характерні ознаки пло­щин особливого положення.

 

 

3. Точки, лінії та плоскі фігури, що розта­шовані у проекційній площині, мають одну зі своїх проекцій на однойменному сліду пло­щини. Таку властивість використано для про­ведення проекційної площини через точку або пряму. Для цього один зі слідів площини проводять через однойменну проекцію точ­ки або прямої.

 

Належність прямої і точки площині

 

1. Пряма належить площині, якщо вона про­ходить: через дві точки, які належать цій пло­щині; через точку, яка належить цій площині і паралельна прямій, що розташована в цій площині або паралельній їй.

Якщо площина задана слідами, то пряма належить площині, якщо сліди прямої розта­шовані на однойменних слідах площини; пря­ма паралельна одному зі слідів цієї площини і має з іншим слідом спільну точку.

2. Точка належить площині, якщо вона на­лежить будь-якій прямій цієї площини.

 

Перетин прямої з площиною

1. Для побудови точки перетину прямої з площиною загального положення необхідно (рис. 3.7, 3.8):

Рис. 3.7

Рис. 3.8

 

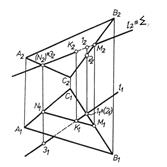
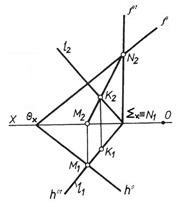
а) через задану пряму l (l₁,l₂) провести де­яку допоміжну площину ;

б) побудувати пряму МN (М₁N₁, М₂N₂) пе­ретину заданої площини з допоміжною;

в) визначити положення точки К (K₁, К₂) перетину прямих: заданої l і побудованої МN.

2. При побудові точки перетину прямої з площиною особливого положення побудова спрощується, оскільки одна з проекцій точки перетину міститься на прямій, у вигляді якої площина проекціюється на ту чи іншу пло­щину проекцій. На рис. 3.9 побудовано точку перетину
К (K₁, К₂) прямої l з горизон­тально-проекційною площиною ( AВС).

Рис. 3.9

 

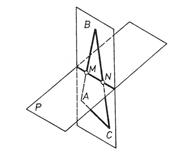
Перетин площин

Задачу на перетин двох площин довільно­го положення розв'язують двома способами:

1) побудувати точки перетину двох прямих однієї площини з іншою площиною, тобто двічі використати алгоритм пошуку точки перети­ну прямої з площиною. На рис. 3.10 площи­на, задана трикутником АВС, перетинається з площиною Р по прямій MN;

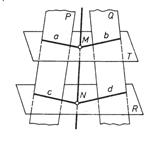
Рис. 3.10

2) використавши дві допоміжні січні пло­щини особливого положення, побудувати лі­нії їх перетину з заданими площинами. Дві відповідні точки перетину цих ліній визнача­ють шукану пряму перегину заданих площин. На рис. 3.11 задані площини Р і Q перетинаються по пря

мій MN. Використано допомі­жну площину Т, яка перетинається з площи­нами Р і Q відповідно по прямих а і b, та до­поміжну площину R, яка перетинається з пло­щинами Р і Q відповідно по прямих с і d.

Рис. 3.11

Завдання 7. Перетин площин

 

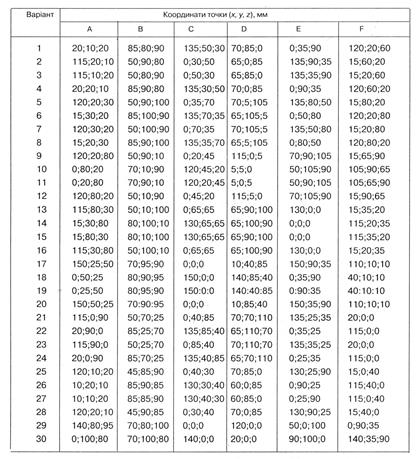
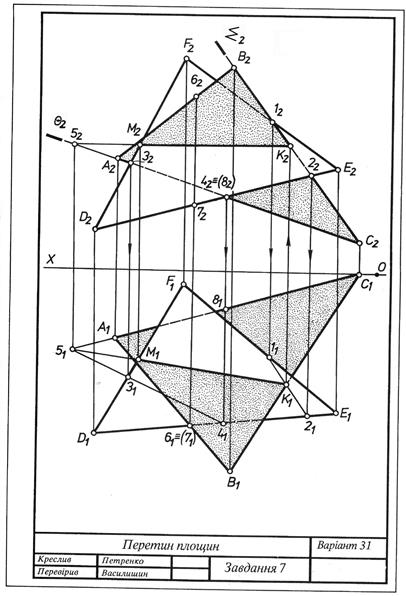
Побудувати лінію перетину площин, заданих трикутниками АВС I DEF. Визначити взаємну видимість площин.

Дані до завдання взяти з табл. 3.3.

Приклад виконання завдання подано на рис. 3.14.

 

Таблиця 3.3

 

 

Рис. 3.14

 

Мета і задачі вивчення теми

Опанувати знаннями утворення многогранник поверхонь, методами побудови креслень многогранників, та знаходити лінії перетину многогранників площинами і перетину многогранників між собою.

 

Грані поверхні

1. Многогранною називається поверхня, утворена частинами перетинних площин.

2. Декілька площин.(але не менше трьох), які перетинаються в якійсь точці, утворюють пірамідальну поверхню (рис. 6.1.). Ця точка (на рис. 4.1 — точка S) є вершиною, в якій перетинаються всі ребра піраміди (на рис. 4.1 —ребрао, a, b,с, d).

 

Рис. 6.1

 

3. Призматична поверхня є окремим ви­падком пірамідальної з невласною верши­ною. Всі ребра такої поверхні взаємно пара­лельні (рис.6.2).

Рис. 6.2

Многогранники

1. Многогранником називається тіло, об­межене многогранною поверхнею.

2. Сукупність усіх ребер і вершин много-гранника є його сіткою.

3. Якщо многогранник розташований з одного боку площини будь-якої його грані, то він називається випуклим.

4. Для отримання проекцій многогранника будують проекції його сітки (рис. 6.3).

Рис. 6.3

5. Пірамідою називають многогранник, усі грані якого, крім однієї, мають спільну верши­ну; її називають вершиною піраміди. Звичай­но піраміду задають на кресленні проекція­ми її основи і вершини (рис. 4.4), а зрізану

 

піраміду — проекціями обох основ (рис. 6.4). Якщо висота піраміди проходить через центр основи піраміди, то піраміда вважається пря­мою. Пряму піраміду називають правильною, якщо її основа — правильний многокутник.

Рис. 6.4

6. Призма — це многогранник, обмежений призматичною поверхнею і двома площинат ми, паралельними між собою, але не парале­льними ребрам призми. Ці дві грані (рівні многокутники) називаються основами призми. Якщо основи не паралельні між со­бою, призма є зрізаною.

7. Многогранники, в яких усі ребра, грані, плоскі, двогранні та просторові кути рівні між собою, називаються правильними випуклими многогранниками (тілами Платона).

Існує п'ять таких тіл:

а) тетраедр (чотиригранник), гранями яко­го є чотири рівносторонні трикутники;

б) октаедр (восьмигранник), гранями яко­го є вісім рівносторонніх трикутників;

в) ікосаедр (двадцятигранник), утворений з двадцяти рівносторонніх трикутників;

г) гексаедр (шестигранник), або куб, гра­нями якого є шість квадратів;

д) додекаедр (дванадцятигранник), утворе­ний з дванадцяти правильних п'ятикутників.

Навколо всіх правильних многогранників можна описати сферу.

 

ТЕМА. КРИВІ ПОВЕРХНІ

7.1. Мета і задачі вивчення теми:

Опанувати методами побудови і аналізу криволінійних поверхонь та навчитися будувати лінії перетину поверхонь площинами.

 

Загальні відомості

1. Основні способи задання поверхні:

а) аналітичний; поверхня розглядається як неперервна двопараметрична (двовимірна) множина точок. Координати точок цієї множи­ни задовольняють деяке рівняння F (х, у,z) = 0 — многочлен n-го степеня. Довільна пряма в за­гальному випадку перетинає поверхню n-го степеня в n точках (справжніх або уявних);

б) кінематичний; поверхня розглядається як неперервна множина положень деякої лінії, що переміщається в просторі за певним законом. Лінії, які утворюють поверхню, називаються твірними. Закон переміщення твірної у прос­торі доцільно задавати нерухомими лініями, які називаються напрямними; ці лінії твірна перетинає в будь-якому своєму положенні;

в) задання поверхні каркасом — множиною ліній, які заповнюють поверхню так, що через кожну точку поверхні проходить одна лінія каркаса. Каркаси поверхонь поділяються на точкові та лінійчаті.

2. Поверхня вважається заданою на крес­ленні, якщо відносно будь-якої точки, заданої на тому ж кресленні, можна однозначно ви­значити, чи належить точка цій поверхні, чи ні.

3. Кожну поверхню вигідно задавати за допомогою визначника—сукупності незале­жних геометричних умов, що визначають цю поверхню в просторі. Визначник складаєть­ся з двох частин: геометричної, в якій зада­ються деякі основні елементи та величини, й алгоритмічної, яка свідчить про характер змі­ни форми твірної і закону її переміщення.

4. Поверхні, твірною яких є пряма лінія, на­зиваються лінійчатими. Нелінійчаті, або криві поверхні утворюються за допомогою криво­лінійних твірних.

5. Усі поверхні можна поділити на розгор-тні й нерозгортні. До розгортних належать ті, які можна розгорнути без деформації — су­містити з площиною так, що всі елементи поверхні зображаються у справжній величині. Нерозгортні поверхні при розгортанні не можна сумістити з площиною.

Перетин поверхонь площиною

1. Лінія перетину многогранника площи­ною визначається або за точками перетину ребер многогранника, або за лініями пере­тину граней многогранника з цією площиною. У першому випадку („спосіб ре­бер”) знаходимо точку перетину прямої з площиною, у другому („спосіб граней”) — визначаємо лінію перетину площин.

2. Многокутник, утворений від перетину многогранника площиною, називається фігу­рою перерізу. Кількість сторін многокутника перерізу дорівнює кількості граней, які пере­тинаються січною площиною.

3. При перетині кривих поверхонь площи­ною в загальному випадку криві лінії утво­рюються шляхом знаходження точок перети­ну твірних поверхні з січною площиною (рис. 7.1). Якщо ж крива поверхня нелінійчата, то для побудови лінії перетину такої поверхні площиною необхідно застосовувати допомі­жні площини (рис. 7.2). Точки шуканої лі­нії знаходять на перетині ліній, по яких допо­міжні січні площини перетинають поверхню і площину. Здебільшого слід користуватися проекційними площинами, оскільки вони пе­ретинають поверхні по лініях, які легко побу­дувати, — прямих і колах.

 

Рис. 7.1 Рис. 7.2

 

ТЕМА. ПЕРЕТИН ПОВЕРХОНЬ

Мета і задачі вивчення теми

Опанувати способами побудови ліній перетину криволінійних поверхонь між собою та перетину криволінійних поверхонь з многогранниками.

КОНТРОЛЬНІ ПИТАННЯ ЩОДО ЗАХИСТУ ЗАВДАНЬ

Тема: Проеціювання площин.

1. Які ви знайете способи задання площин на кресленнях?

2. Як класифікуються площини?

3. Як визначити належність точки та прямої до площини?

4. Як визначити кути нахилу площини до площин проекцій?

5. Визначити алгоритм побудови точки перетину прямої з площиною.

6. Які особливості визначення точки перетину площин заданих слідами?

7. Як визначити точку перетину прямої з площиною особливого положення?

8. Як визначити лінію перетину площин довільного положення?

 

Тема: Криві поверхні

1. Які поверхні називають лінійчатими та не лінійчатими?

2. Які поверхні називаються розгортними та перегортними?

3. В чому сутність методу твірних при побутові лінії перетину поверхонь площинами?

4. В чому сутність методу допоміжних січних площин?

5. Які положення допоміжних січних площин бути по відношенню до поверхні?

Тема: Перетин поверхонь

1. В чому сутність методу допоміжних площин?

2. Межі використання цього методу.

3. В чому сутність методу допоміжних січних куль?

4. Межі використання цього методу.

5. Особливості побудови лінії перетину кривої поверхні з многогранником.

 

СПИСОК ЛІТЕРАТУРИ

 

1. В.О. Гордон «Начертательная геометрия», М.-«Наука»,
   1988 г. – 272 с.
2. С.А. Фролов «Начертательная геометрия», М.- «Машиностроение», 1983 г.
3. Х.А. Арустамов. Сборник задач по начертательной геометрии. – М. Машиностроение, 1965 г. – 375 с.
4. А.К. Рудаев. Сборник задач по начертательной геометрии. – М. Физмат. 1962 г., -344 с.
5. С.А. Фролов Сборник задач по начертательной геометрии. – М. Машиностроение. 1987 г., -176 с.

 

Навчальне видання

 

 

МЕТОДИЧНІ ВКАЗІВКИ

до виконання контрольних робіт студентами заочної форми навчання та індивідуальних завдань студентами денної форми навчання з розділу нарисна геометрія дисципліни „ІНЖЕНЕРНА ГРАФІКА”

студентів всіх спеціальностей)

 

У к л а д а чі:

Микола Іванович Гуліда

Людмила Георгіївна Холіна

 

 

Редактор В.Н.Полчачов

Комп'ютерна верстка В.М. Закотянський

 

 

Підписано до друку___________

Формат 60 х 84 ¹/₁₆. Папір друк. Гарнітура Times

Друк офсетний. Умов. др. Арк. Обл.вид.арк.

Тираж прим. Вид. №_____ Зам. ______Ціна договірна

 

 

Видавництво Сєвєродонецького технологічного інституту

СНУ імені Володимира Даля

 

 

Адрес видавництва: 93400, г.Сєвєродонецьк, Луганська обл. пр.Радянський, 59-а, головний корпус

Телефон: [phone]

Е-mail: sti@ sti.lg.ua

 

 

МЕТОДИЧНІ ВКАЗІВКИ

до виконання контрольних робіт студентами

заочної форми навчання та індивідуальних завдань

студентами денної форми навчання з розділу нарисна геометрія дисципліни

„ІНЖЕНЕРНА ГРАФІКА”

(для студентів всіх спеціальностей)

 

 

СЄВЄРОДОНЕЦЬК 2005

УДК 22.151.3

 

Методичні вказівки до виконання контрольних робіт студентами заочної форми навчання та індивідуальних завдань студентами денної форми навчання з розділу нарисна геометрія дисципліни „Інженерна графіка” студентів всіх спеціальностей. Укл. М.І. Гуліда, Л.Г. Холіна.- Сєвєродонецьк: Вид-во СТІ 2005. 78 –с.

 

 

Приведені матеріали, необхідні для виконання контрольних робіт та індивідуальних завдань з дисципліни „Інженерна графіка”. Описані основні теоретичні положення з розділу „нарисна геометрія”, мета та задачі тем розділу. Складені варіанти завдань та наведені приклади виконання їх, дані контрольні питання по темам розділу.

 

 

Укладачі М.І. Гуліда

Л.Г. Холіна

 

Відповідальний за випуск О.Г. Архіпов

 

Рецензент О.О. Дорогін

 

 

Затверджено Вченою радою інституту.

Протокол №___ від „____” ___________ 2005р.

 

 

Голова Вченої ради,

К.т.н., доцент О.Г. Архіпов

ЗМІСТ

1. Область застосування..................................................... 4

2. Тема. Проекція точки і прямої....................................... 4

3. Тема. Проекціювання площин........................................ 19

4. Тема. Перпендикулярність і паралельність геометричних елементів.......................................................................... 30

5. Тема. Способи перетворення креслення....................... 38

6. Тема. Грані поверхні та многогранники....................... 45

7. Тема. Криві поверхні....................................................... 51

8. Тема. Перетин поверхонь............................................... 61

9. Порядок оформлення та захисту завдань, критерії
оцінки................................................................................ 74

10. Контрольні питання щодо захисту завдань.................. 74

Список літератури........................................................... 77

ОБЛАСТЬ ЗАСТОСУВАННЯ

 

Методичні вказівки призначені для виконання контрольних робіт студентами заочниками та індивідуальних завдань студентами денної форми навчання при вивченні дисципліни „Нарисна геометрія” або аналогічних розділів „Інженерної графіки”.

 

ТЕМА: ПРОЕКЦІЇ ТОЧКИ І ПРЯМОЇ

 

2.1. Мета і задачі вивчення теми:

 

Опанувати методи проеціювання точки і прямої лінії залежно від їх розташування в просторі, а також визначити основні параметри об’єктів проеціювання.