
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Відстань від точки до прямоїСодержание книги Поиск на нашем сайте
Розглянемо точку
Означення. Відстанню від точки
Відстань від точки
Приклад 1.
Дано координати вершин трикутника
Знайти:
1. Довжину сторони 2. Рівняння сторін 3. Внутрішній кут 4. Рівняння медіани 5. Рівняння висоти 6. Систему лінійних нерівностей, які визначають трикутник
Зробити рисунок. Розв’язання.
Побудуємо трикутник
1. Визначимо довжину сторони АВ за формулою відстані між двома точками на площині:
отже,
2. Одержимо рівняння сторін
Скористаємось рівнянням прямої, що проходить через дві задані точки:
Одержимо
Скористуємось тепер основною властивістю пропорції (добуток крайніх членів дорівнює добутку середніх членів пропорції):
або
Для того, щоб одержати рівняння прямої
Аналогічно, для прямої
Отже,
3. Відомо, що тангенс кута
4. Медіаною трикутника називають відрізок, який сполучає вершину трикутника з серединою протилежної сторони.
Оскільки
Визначимо координати точки
отже точка
Застосуємо тепер рівняння прямої, що проходить через дві задані точки:
5. Висотою трикутника називають перпендикуляр, опущений з вершини трикутника на протилежну сторону.
Оскільки
Оскільки Підставимо тепер кутовий коефіцієнт
Одержимо:
Довжина висоти
Точка
загальне рівняння прямої
6. Множину точок
Підставимо в рівняння прямої
а отже нерівність, яка визначає першу з півплощин буде:
Загальне рівняння
Підставляємо в це рівняння координати точки
Таким чином, друга півплощина визначається нерівністю
Одержимо рівняння прямої
Підставимо в це рівняння координати точки
Отже, нерівність, яка визначає третю півплощину, має вигляд:
а система одержаних нерівностей, яка визначає множину точок трикутника:
Питання для самоперевірки
1. За якою формулою визначається відстань між двома точками на площині?
2. За якими формулами обчислюються координати точки, що ділить заданий відрізок у заданому відношенні?
3. Що називається рівнянням лінії на площині
4. Який вид має рівняння прямої з кутовим коефіцієнтом?
5. Який геометричний зміст параметрів
6. Запишіть загальне рівняння прямої. Як знайти кутовий коефіцієнт цієї прямої?
7. Який вид має рівняння прямої у відрізках на осях? Рівняння прямої, що проходить через дві задані точки?
8. Як знайти кут між двома прямими?
9. Сформулюйте умову паралельності прямих.
10. Яка умова перпендикулярності прямих?
11. Як знайти точку перетину двох прямих?
12. Як побудувати пряму, задану відповідним рівнянням?
13. Як знайти відстань від точки до прямої?
Задачі до розділу 1
1. Знайти рівняння прямої, що проходить через точку перетину прямих
2. Дана пряма
3. Знайти кут між прямими
4. Знайти відстань від точки
5. Записати рівняння прямої, що проходить через точку
6. Скласти рівняння прямої, яка відтинає на осі ординат відрізок, величина якого дорівнює
7. Знайти координати точки
8. Знайти точку перетину прямих
9. Приведіть рівняння прямої
10. Знайти відстань від точки
11. Скласти різні види рівняння прямої, що проходить через точку
12. Скласти рівняння прямої, що проходить через точку
13. Знайти відстань від середини відрізка, що сполучає точки
14. Визначити периметр трикутника з вершинами
15. Визначити координати середин сторін трикутника з вершинами
16. Записати рівняння прямої, яка проходить через початок системи координат і нахилена до осі
17. Серед прямих
18. В точках перетину прямої
19. Знайти вершини трикутника, сторони якого задані рівнянням
20. Дана пряма
В задачах 21 – 40 дано координати вершин трикутника
Вимагається знайти:
1) периметр трикутника;
2) рівняння сторін
3) внутрішній кут
4) рівняння медіани
5) рівняння висоти
6) рівняння прямої, що проходить через точку
7) систему лінійних нерівностей, що визначають трикутник
Зробити рисунок.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
РОЗДІЛ 2. КРИВІ ДРУГОГО ПОРЯДКУ
|
||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.01 с.) |

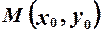 і пряму
і пряму 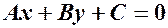 .
.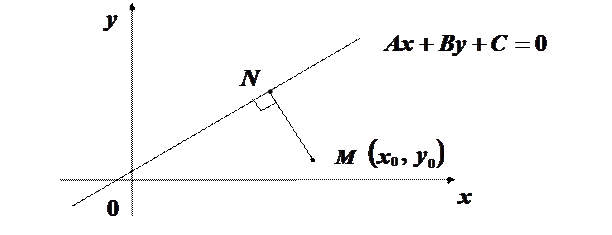
 до прямої
до прямої  , заданої рівнянням
, заданої рівнянням 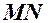 , опущеного з точки
, опущеного з точки 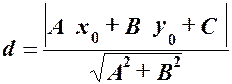 .
. :
: 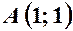 ,
, 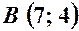 ,
, 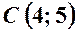 .
. ;
; в загальному вигляді та з кутовим коефіцієнтом.
в загальному вигляді та з кутовим коефіцієнтом. ;
; ;
; та її довжину;
та її довжину;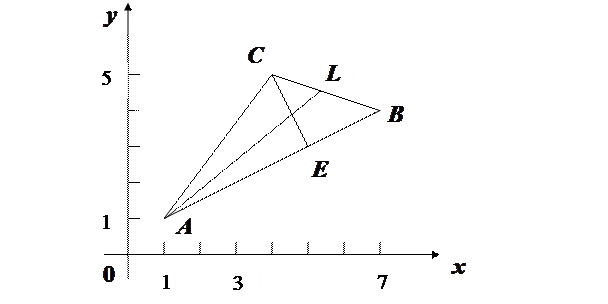

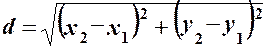 .
.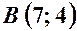 ,
,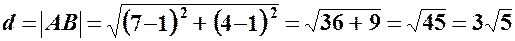 (од.).
(од.).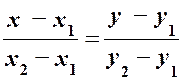 .
.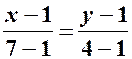 , звідки
, звідки 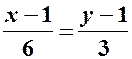 , або
, або 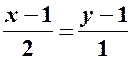 .
.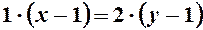 ,
,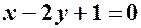 – загальне рівняння прямої
– загальне рівняння прямої  через
через  :
: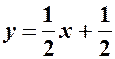 – рівняння
– рівняння 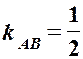 .
.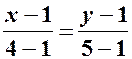 , або
, або 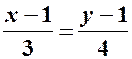 .
.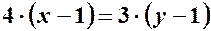 ,
, 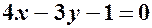 – загальне рівняння прямої
– загальне рівняння прямої 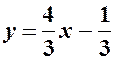 – рівняння
– рівняння 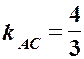 .
. між двома прямими, кутові коефіцієнти яких відповідно дорівнюють
між двома прямими, кутові коефіцієнти яких відповідно дорівнюють 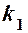 і
і 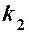 , обчислюють за формулою:
, обчислюють за формулою: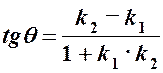 .
.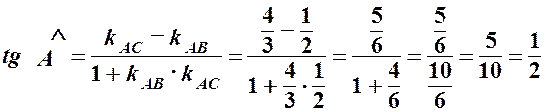 ,
,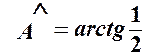 .
.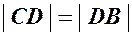 .
. : скористуємось для цього формулами ділення відрізка навпіл:
: скористуємось для цього формулами ділення відрізка навпіл: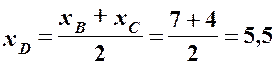 ,
, 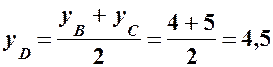 ,
,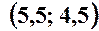 .
.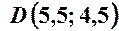 .
.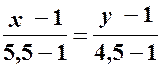 ;
; 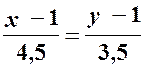 ;
;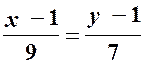
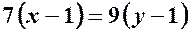 ;
;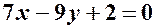 – загальне рівняння медіани
– загальне рівняння медіани 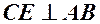 . Одержимо рівняння висоти
. Одержимо рівняння висоти 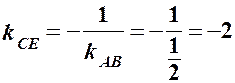 .
.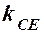 та координати точки
та координати точки 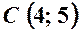 в рівняння:
в рівняння: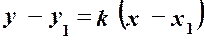 .
.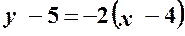 ;
; 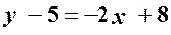 ;
; 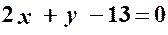 – рівняння висоти
– рівняння висоти  до прямої
до прямої 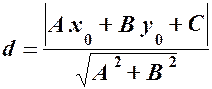 .
.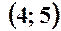 ;
;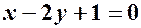 , тоді:
, тоді: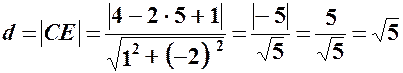 (од.).
(од.).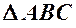 можна розглядати як перетин трьох площин, з яких перша обмежена прямою
можна розглядати як перетин трьох площин, з яких перша обмежена прямою 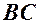 і містить точку
і містить точку 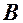 .
.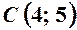 , маємо тоді:
, маємо тоді: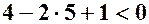 ,
,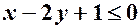 .
.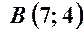 :
: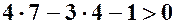 .
.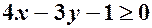 .
.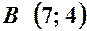 ,
, 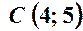
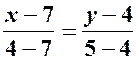 ;
; 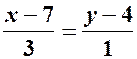 ;
; 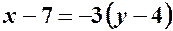 ;
;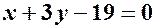 – загальне рівняння прямої
– загальне рівняння прямої 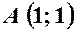 :
: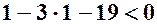 .
.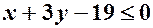 ,
,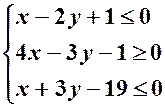 .
. ?
? і
і  в рівнянні прямої з кутовим коефіцієнтом?
в рівнянні прямої з кутовим коефіцієнтом?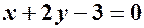 і
і  і паралельна осі
і паралельна осі  .
.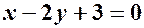 . Скласти рівняння прямої, що проходить через точку
. Скласти рівняння прямої, що проходить через точку  і перпендикулярна до заданої прямої.
і перпендикулярна до заданої прямої. і
і  .
. до прямої
до прямої  .
. паралельно прямій
паралельно прямій  .
. і утворює з віссю
і утворює з віссю  .
. , яка ділить відрізок
, яка ділить відрізок  у відношенні
у відношенні  , якщо
, якщо  ,
,  .
. і
і  .
. до вигляду у відрізках на осях. Побудуйте пряму.
до вигляду у відрізках на осях. Побудуйте пряму. ,
, 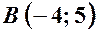 ,
,  .
. , паралельно прямій
, паралельно прямій  .
. та відтинає на осях координат однакові відрізки.
та відтинає на осях координат однакові відрізки. і
і  до прямої
до прямої  .
. ,
, 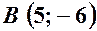 ,
,  .
. ,
,  ,
,  .
. ?
?  ?
? ,
,  ,
,  ,
,  визначити паралельні та перпендикулярні.
визначити паралельні та перпендикулярні. з осями координат проведені перпендикуляри до цієї прямої. Записати їх рівняння.
з осями координат проведені перпендикуляри до цієї прямої. Записати їх рівняння. ,
,  ,
,  .
. . Які з точок
. Які з точок  ,
, 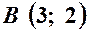 ,
,  ,
,  ,
,  ,
,  лежать на цій прямій?
лежать на цій прямій?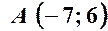 ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
, 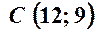 .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
, 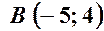 ,
,  .
.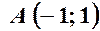 ,
,  ,
,  .
. ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
, 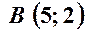 ,
,  .
. ,
,  .
. ,
,  ,
, 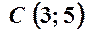 .
.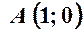 ,
,  ,
,  .
. ,
,  ,
,  .
.


