
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лінійні операції над векторамиСодержание книги Поиск на нашем сайте
Додавання векторів.
Означення. Сумою n векторів, розміщених послідовно (початок наступного вектора співпадає з кінцем попереднього), називається вектор, який сполучає початок першого вектор-доданка з кінцем останнього вектор-доданка.
У випадку двох векторів їх суму можна визначити за правилом трикутника або за правилом паралелограма.
Означення. Сумою двох векторів, розташованих послідовно, називається вектор, який з’єднує початок першого з кінцем другого (правило трикутника).
Означення. Сумою двох векторів, які мають спільний початок, називають вектор, що співпадає з діагоналлю паралелограма, побудованого на цих векторах (правило паралелограма).

Множення вектора на число.
Означення. Добутком вектора
Означення. Одиничним вектором (ортом) вектора
ПРОЕКЦІЯ ВЕКТОРА НА ВІСЬ
Означення. Проекцією точки
Означення. Проекцією вектора
Означення. Кутом між вектором і віссю називають найменший кут
Т е о р е м а. Проекція вектора
РОЗКЛАД ВЕКТОРА ЗА КООРДИНАТНИМИ ОРТАМИ
Розглянемо у просторі прямокутну систему координат Нехай точка
Означення. Декартові прямокутні координати точки
Позначимо проекції вектора
Одержимо
Вектор
Модуль вектора
Позначимо кути, які вектор
Маємо тепер
Косинуси
Напрямні косинуси задовольняють умову:
Зауважимо, якщо
то
СКАЛЯРНИЙ ДОБУТОК ВЕКТОРІВ ТА ЙОГО ВЛАСТИВОСТІ
Означення. Скалярним добутком векторів
Скалярний добуток двох векторів має такі в л а с т и в о с т і:
1. Переставний закон: 2. Розподільний закон: 3. Сполучний закон: 4. Якщо 5. Скалярний квадрат вектора дорівнює квадрату його модуля:
6. Вектори перпендикулярні тоді і лише тоді, коли їх скалярний добуток дорівнює нулю. Отже, якщо
7. Скалярні добутки ортів:
СКАЛЯРНИЙ ДОБУТОК ДВОХ ВЕКТОРІВ, ЗАДАНИХ КООРДИНАТАМИ Нехай задано два вектори:
Обчислимо скалярний добуток
оскільки
Отже, маємо:
Наслідки.
1.
2.
3. Умова перпендикулярності векторів:
Умова перпендикулярності векторів:
Приклад 8.
Дано координати точок
Вимагається: 1) записати вектори 2) знайти кут між векторами 3) знайти проекції:
Розв’язання. 1) Якщо відомі координати точки
або
Маємо
Остаточно:
Модуль вектора
2) Скористуємося формулою
3)
Питання для самоперевірки
13. Які вектори називаються колінеарними?
14. Які вектори називаються компланарними?
15. Що називається сумою векторів?
16. Як визначається операція множення вектора на число?
17. Що називається проекцією вектора на вісь?
18. Який розклад вектора за координатними ортами?
19. Дайте означення скалярного добутку двох векторів.
20. Сформулюйте основні властивості скалярного добутку.
21. Як обчислюється скалярний добуток двох векторів в координатній формі?
22. За якою формулою обчислюється кут між двома векторами?, проекція вектора на вектор?
23. Сформулюйте умови паралельності та перпендикулярності векторів. Задачі до розділу 3
В задачах 101–120 дано координати точок
Вимагається: 1) записати вектори
2) знайти кут
3) Знайти проекцію вектора
101.
102.
103.
104.
105.
106.
107.
108.
109.
110.
111.
112.
113.
114.
115.
116.
117.
118.
119.
120.
РОЗДІЛ 4.
|
||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 994; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.008 с.) |


 на скаляр
на скаляр  називається вектор
називається вектор 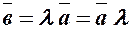 , модуль якого дорівнює добутку
, модуль якого дорівнює добутку  на
на  , а напрям співпадає з напрямом
, а напрям співпадає з напрямом  , і протилежний напряму
, і протилежний напряму  .
. , напрям якого співпадає з напрямом
, напрям якого співпадає з напрямом  .
. на вісь
на вісь 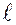 називають основу
називають основу  перпендикуляра
перпендикуляра  , опущеного з точки
, опущеного з точки  (рис. 3.).
(рис. 3.). на вісь
на вісь  , взятий зі знаком „ + ”, якщо вектор
, взятий зі знаком „ + ”, якщо вектор  спів напрямлений з віссю
спів напрямлений з віссю 
 , на який треба повернути вісь, щоб її напрям співпав з напрямом вектора
, на який треба повернути вісь, щоб її напрям співпав з напрямом вектора  .
.
 на косинус кута між вектором та віссю.
на косинус кута між вектором та віссю. ,
,  .
. . Нехай
. Нехай  – орт осі
– орт осі  ,
,  – орт осі
– орт осі  ,
,  – орт осі
– орт осі  .
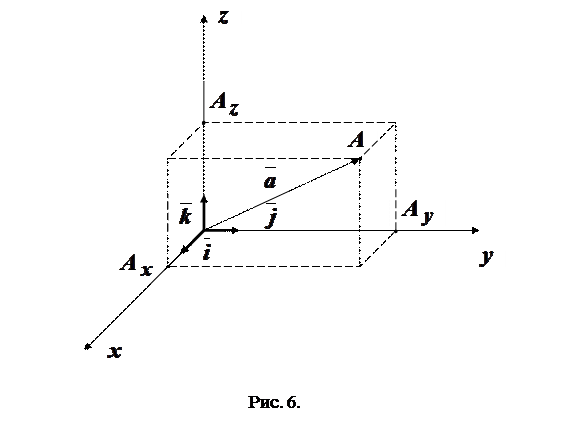
. – деяка довільна точка простору. Вектор
– деяка довільна точка простору. Вектор  називають радіус-вектором точки
називають радіус-вектором точки  .
. на осі відповідно
на осі відповідно  (абсциса),
(абсциса),  (ордината),
(ордината),  (апліката), тоді
(апліката), тоді ,
, ,
, ,
, .
.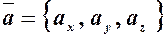 .
.
 .
.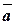 утворює з координатними осями так:
утворює з координатними осями так: ,
,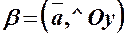 ,
, (рис. 7).
(рис. 7).
 ,
, 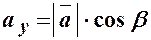 ,
,  .
. ,
,  ,
,  називають напрямленими косинусами радіус-вектора
називають напрямленими косинусами радіус-вектора  ,
,  ,
,  .
. .
. ,
,  ,
,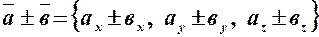 ,
, .
. називають число, яке дорівнює добутку модулів цих векторів на косинус кута між ними.
називають число, яке дорівнює добутку модулів цих векторів на косинус кута між ними.
 .
. .
. .
.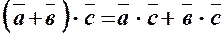 .
. .
. .
. .
. , то
, то  і навпаки.
і навпаки. ,
, 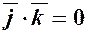 ,
,  ,
,  ,
,  ,
,  .
.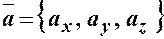 і
і  ; інакше
; інакше  ,
,  .
. .
.

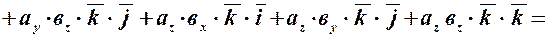
 ,
, .
. .
. .
. .
. .
. .
.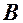 ,
,  .
. і
і  в координатній формі та знайти модулі цих векторів;
в координатній формі та знайти модулі цих векторів; ,
,  .
. ,
,  ,
,  .
. і точки
і точки  , то вектор
, то вектор  ,
, .
. ,
, .
. ,
, .
. обчислюємо за формулою
обчислюємо за формулою .
. .
.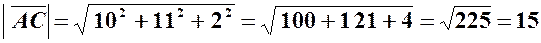 .
.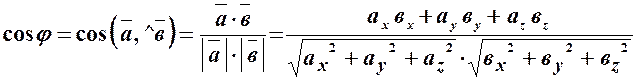 ,
, .
. .
. .
.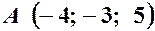 ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
, 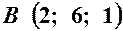 ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
.


