
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналітична геометрія на площині та у просторі.Стр 1 из 7Следующая ⇒
Дьяченко Н.К. АНАЛІТИЧНА ГЕОМЕТРІЯ НА ПЛОЩИНІ ТА У ПРОСТОРІ. ЕЛЕМЕНТИ ВЕКТОРНОЇ АЛГЕБРИ. Навчальний посібник
Дніпропетровськ Дьяченко Н.К.
Аналітична геометрія на площині та у просторі. Елементи векторної алгебри: Навчальний посібник/ Дніпропетровський державний аграрний університет – Дніпропетровськ, 2009 – 78 с.
У навчальному посібнику розглянуто основні поняття і положення аналітичної геометрії на площині та у просторі, а також елементи векторної алгебри. Розібрано типові задачі, а також наведені завдання для самостійного розв’язування. Посібник буде корисним для студентів заочної форми навчання економічних спеціальностей, а також для студентів очної форми навчання при підготовці до модульної роботи з аналітичної геометрії.
РОЗДІЛ 1. ПРЯМА НА ПЛОЩИНІ
ВІДСТАНЬ МІЖ ДВОМА ТОЧКАМИ НА ПЛОЩИНІ
Нехай задано точки
З
Отже, відстань між двома точками на площині
Відстань точки
ДІЛЕННЯ ВІДРІЗКА В ЗАДАНОМУ ВІДНОШЕННІ
Дано точки
Вимагається знайти координати точки
Координати точки
Зауваження. Координати середини відрізка
ПОНЯТТЯ РІВНЯННЯ ЛІНІЇ НА ПЛОЩИНІ
Нехай на площині задано декартову прямокутну систему координат
Означення. Рівняння
РІВНЯННЯ ПРЯМОЇ НА ПЛОЩИНІ
Рівняння прямої з кутовим коефіцієнтом. Означення. Кутом нахилу прямої до осі
Означення. Кутовим коефіцієнтом прямої називається тангенс кута нахилу цієї прямої до осі
Рівняння прямої з кутовим коефіцієнтом має вид:
Числовий параметр
Розглянемо деякі частинні випадки.
1) Якщо
2) Якщо
3) Якщо
Загальне рівняння прямої. Т е о р е м а. Кожне рівняння першого ступеня відносно х і у, тобто рівняння виду
Рівняння
називають загальним рівнянням прямої.
Частинні випадки.
1)
2)
3) 4)
5)
Рівняння прямої, що проходить через задану точку в заданому напрямі. Нехай задано точку
називають рівнянням прямої, що проходить через задану точку в заданому напрямі.
Рівняння прямої, що проходить через дві задані точки. Нехай задано точки
Використаємо рівняння (3). Підставимо в це рівняння координати точки Маємо
Підставимо цей кутовий коефіцієнт в рівняння (3).
Дістанемо
звідки
рівняння прямої, що проходить через дві задані точки.
В рівнянні (4) припускаємо, що
Якщо
Якщо
Рівняння прямої у відрізках на осях. Рівняння прямої у відрізках на осях має вид:
Параметр
КУТ МІЖ ДВОМА ПРЯМИМИ. ТОЧКА ПЕРЕТИНУ ДВОХ ПРЯМИХ
Нехай задано дві прямі:
Вимагається знайти координати точки перетину цих прямих.
Оскільки точка перетину прямих лежить як на першій, так і на другій прямій, то координати цієї точки повинні задовольняти кожне з рівнянь прямих. Отже, для того, щоб знайти координати точки перетину прямих, треба розв’язати сумісно систему рівнянь цих прямих:
Зауваження. 1. Якщо
2. Якщо
Питання для самоперевірки
1. За якою формулою визначається відстань між двома точками на площині?
2. За якими формулами обчислюються координати точки, що ділить заданий відрізок у заданому відношенні?
3. Що називається рівнянням лінії на площині
4. Який вид має рівняння прямої з кутовим коефіцієнтом?
5. Який геометричний зміст параметрів
6. Запишіть загальне рівняння прямої. Як знайти кутовий коефіцієнт цієї прямої?
7. Який вид має рівняння прямої у відрізках на осях? Рівняння прямої, що проходить через дві задані точки?
8. Як знайти кут між двома прямими?
9. Сформулюйте умову паралельності прямих.
10. Яка умова перпендикулярності прямих?
11. Як знайти точку перетину двох прямих?
12. Як побудувати пряму, задану відповідним рівнянням?
13. Як знайти відстань від точки до прямої?
Задачі до розділу 1
1. Знайти рівняння прямої, що проходить через точку перетину прямих
2. Дана пряма
3. Знайти кут між прямими
4. Знайти відстань від точки
5. Записати рівняння прямої, що проходить через точку
6. Скласти рівняння прямої, яка відтинає на осі ординат відрізок, величина якого дорівнює
7. Знайти координати точки
8. Знайти точку перетину прямих
9. Приведіть рівняння прямої
10. Знайти відстань від точки
11. Скласти різні види рівняння прямої, що проходить через точку
12. Скласти рівняння прямої, що проходить через точку
13. Знайти відстань від середини відрізка, що сполучає точки
14. Визначити периметр трикутника з вершинами
15. Визначити координати середин сторін трикутника з вершинами
16. Записати рівняння прямої, яка проходить через початок системи координат і нахилена до осі
17. Серед прямих
18. В точках перетину прямої
19. Знайти вершини трикутника, сторони якого задані рівнянням
20. Дана пряма
В задачах 21 – 40 дано координати вершин трикутника
Вимагається знайти:
1) периметр трикутника;
2) рівняння сторін
3) внутрішній кут
4) рівняння медіани
5) рівняння висоти
6) рівняння прямої, що проходить через точку
7) систему лінійних нерівностей, що визначають трикутник
Зробити рисунок.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
РОЗДІЛ 2. КРИВІ ДРУГОГО ПОРЯДКУ КОЛО
Означення. Коло – геометричне місце точок площини, рівновіддалених від даної точки, що називається центром кола.
Одержимо рівняння кола з центром в точці
Нехай точка
Визначимо відстань між точками
канонічне рівняння кола з центром в точці
Коло радіуса
Якщо в рівнянні (1) розкрити дужки, то одержимо рівняння кола у вигляді:
Як бачимо, для рівняння кола виконуються дві умови: 1) коефіцієнти при 2) відсутній член з добутком координат х ∙ у. Приклад 2. Знайти центр і радіус кола Розв’язання.
Перетворимо ліву частину рівняння, виділимо для цього повні квадрати по змінним
ЕЛІПС
Означення. Еліпсом називається геометричне місце точок площини, сума відстаней від кожної з яких до двох заданих точок (фокусів), є величина стала, дорівнює 2а, більша, ніж відстань між фокусами.
Позначимо відстань між фокусами Виберемо систему координат так, щоб фокуси мали координати
Нехай точка
тоді
Ліву і праву частини останнього рівняння піднесемо до квадрату:
звідки
або
тоді
Згідно з умовою в означенні еліпса
Позначимо
Еліпс, заданий канонічним рівнянням, симетричний відносно осей координат:
точка
Точки перетину еліпса з осями називаються вершинами еліпса.
Отже, еліпс має чотири вершини:
Означення. Ексцентриситетом еліпса називається відношення відстані між фокусами до довжини великої осі.
Оскільки
Ексцентриситет характеризує форму еліпса: якщо
Означення. Директрисами еліпса називають дві прямі, перпендикулярні до фокальної осі еліпса і розміщенні симетрично відносно центра еліпса на відстані
Приклад 3. Побудувати, виписати основні числові характеристики:
Розв’язання. Дане рівняння є канонічним рівнянням еліпса.
Побудуємо прямокутну декартову систему координат на площині. Вздовж осі

Вершини еліпса мають координати:
Визначимо параметр
Фокуси лежать на осі
Ексцентриситет еліпса
Директриси мають рівняння:
Приклад 4.
Скласти канонічне рівняння еліпса, що проходить через точку
Розв’язання.
Канонічне рівняння еліпса має вид:
З урахуванням, що велика піввісь
Оскільки точка Визначимо звідси:
Тепер запишемо шукане канонічне рівняння еліпса:
ГІПЕРБОЛА
Означення. Гіперболою називається геометричне місце точок на площині, абсолютна величина різниці відстаней яких до двох заданих точок – фокусів, є величина стала, дорівнює
Позначимо відстань між фокусами
Нехай точка
Зробивши перетворення, аналогічні тим, що зроблено при виведенні рівняння еліпса маємо:
де
Гіпербола має дві вершини:
Означення. Ексцентриситетом гіперболи називається відношення відстані між фокусами до довжини дійсної осі:
Означення. Асимптотою кривої називають таку пряму з властивістю, що точка, яка віддаляється по кривій у нескінченність, необмежено наближається до цієї прямої.
Гіпербола має дві асимптоти:
Означення. Директрисами гіперболи називаються дві прямі, перпендикулярні до фокусної (дійсної) осі гіперболи і знаходяться на відстані
Означення. Гіпербола, у якої Приклад 5.
Скласти рівняння геометричного місця точок, відношення відстаней яких від даної точки Розв’язання.
В прямокутній декартовій системі координат побудуємо точку
 – довільна точка шуканого геометричного місця точок. – довільна точка шуканого геометричного місця точок.  – перпендикуляр до прямої – перпендикуляр до прямої  . Точка . Точка 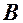 має координати має координати  . .
За умовою задачі
Відстані
тепер маємо:
Ліву і праву частини рівняння розділимо почленно на 5:
Одержане рівняння – канонічне рівняння гіперболи. Дійсна піввісь
Визначимо координати фокусів гіперболи:
Отже, фокуси гіперболи: Ексцентриситет одержаної гіперболи Отже, Директриса гіперболи:
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 879; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.137.243 (0.329 с.) |
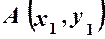 і
і  . Визначимо відстань між ними.
. Визначимо відстань між ними.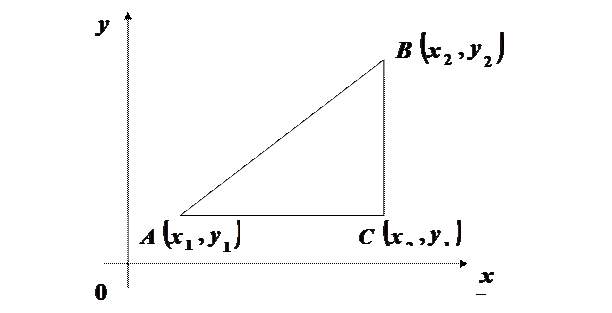
 маємо:
маємо: .
.
 від початку координат знаходимо за формулою
від початку координат знаходимо за формулою  .
.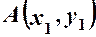 та
та  .
. , яка ділить відрізок
, яка ділить відрізок  у відношенні
у відношенні  , тобто
, тобто .
. .
. знаходимо за формулами
знаходимо за формулами .
. і деяку лінію
і деяку лінію  .
. називають рівнянням лінії (відносно заданої системи координат), якщо рівняння задовольняється координатами
називають рівнянням лінії (відносно заданої системи координат), якщо рівняння задовольняється координатами  і
і  будь-якої точки, яка лежить на лінії і не задовольняється координатами
будь-якої точки, яка лежить на лінії і не задовольняється координатами  називається кут між прямою та віссю
називається кут між прямою та віссю  .
.


 називають початковою ординатою. Параметр
називають початковою ординатою. Параметр  , то рівняння (1) має вигляд
, то рівняння (1) має вигляд  – рівняння прямої, що проходить через початок системи координат.
– рівняння прямої, що проходить через початок системи координат. , то рівняння (1) має вигляд
, то рівняння (1) має вигляд  – рівняння прямої, паралельної осі
– рівняння прямої, паралельної осі  , то рівняння (1) має вигляд
, то рівняння (1) має вигляд  – рівняння осі
– рівняння осі  , визначає на площині пряму лінію.
, визначає на площині пряму лінію.
 ,
,  .
.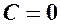 ,
,  . Рівняння (2) тоді матимемо вид
. Рівняння (2) тоді матимемо вид  – рівняння прямої, що проходить через початок системи координат.
– рівняння прямої, що проходить через початок системи координат. ,
,  . Пряма визначається рівнянням
. Пряма визначається рівнянням  , або
, або  – пряма, яка паралельна осі
– пряма, яка паралельна осі  ,
,  . В цьому випадку рівняння (2) буде мати вид
. В цьому випадку рівняння (2) буде мати вид  , звідки
, звідки  – рівняння прямої, паралельної осі
– рівняння прямої, паралельної осі  .
. ,
,  , рівняння (2) має вигляд:
, рівняння (2) має вигляд: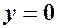 – рівняння осі
– рівняння осі 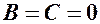 ,
,  , рівняння (2) має вигляд:
, рівняння (2) має вигляд: – рівняння осі
– рівняння осі 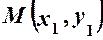 , через яку проходить пряма і кутовий коефіцієнт
, через яку проходить пряма і кутовий коефіцієнт  цієї прямої, тоді рівняння
цієї прямої, тоді рівняння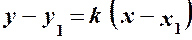
 і
і  . Вимагається скласти рівняння прямої, що проходить через ці точки.
. Вимагається скласти рівняння прямої, що проходить через ці точки. .
.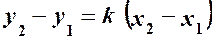 , звідки
, звідки  – кутовий коефіцієнт прямої, яка проходить через дві задані точки.
– кутовий коефіцієнт прямої, яка проходить через дві задані точки. ,
,
 ,
,  , інакше, це рівняння не має змісту.
, інакше, це рівняння не має змісту. , то будемо мати
, то будемо мати  – пряма, паралельна осі ординат.
– пряма, паралельна осі ординат. , то маємо пряму
, то маємо пряму  – пряма паралельна осі абсцис.
– пряма паралельна осі абсцис.

 в цьому рівнянні – абсциса точки перетину прямої з віссю
в цьому рівнянні – абсциса точки перетину прямої з віссю 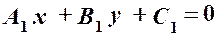 і
і 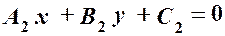 .
.
 , то прямі паралельні, точок перетину немає.
, то прямі паралельні, точок перетину немає. , то прямі зливаються, і таким чином точок перетину безліч.
, то прямі зливаються, і таким чином точок перетину безліч.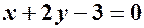 і
і  і паралельна осі
і паралельна осі 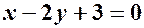 . Скласти рівняння прямої, що проходить через точку
. Скласти рівняння прямої, що проходить через точку  і перпендикулярна до заданої прямої.
і перпендикулярна до заданої прямої. і
і  .
. до прямої
до прямої  .
. паралельно прямій
паралельно прямій  .
. і утворює з віссю
і утворює з віссю  .
. , яка ділить відрізок
, яка ділить відрізок  у відношенні
у відношенні  , якщо
, якщо  ,
,  .
. і
і  .
. до вигляду у відрізках на осях. Побудуйте пряму.
до вигляду у відрізках на осях. Побудуйте пряму. ,
, 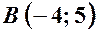 ,
,  .
. , паралельно прямій
, паралельно прямій  .
. та відтинає на осях координат однакові відрізки.
та відтинає на осях координат однакові відрізки. і
і  до прямої
до прямої  .
. ,
, 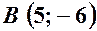 ,
,  .
. ,
,  ,
,  .
. ?
?  ?
? ,
,  ,
,  ,
,  визначити паралельні та перпендикулярні.
визначити паралельні та перпендикулярні. з осями координат проведені перпендикуляри до цієї прямої. Записати їх рівняння.
з осями координат проведені перпендикуляри до цієї прямої. Записати їх рівняння. ,
,  ,
,  .
. . Які з точок
. Які з точок  ,
, 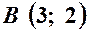 ,
,  ,
,  ,
,  ,
,  лежать на цій прямій?
лежать на цій прямій? .
. в загальному вигляді та їх кутові коефіцієнти;
в загальному вигляді та їх кутові коефіцієнти; ;
; та її довжину;
та її довжину;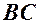 ;
;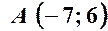 ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
, 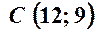 .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
, 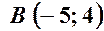 ,
,  .
.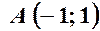 ,
,  ,
,  .
. ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
, 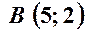 ,
,  .
. ,
,  .
. ,
,  ,
, 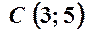 .
.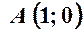 ,
,  ,
,  .
. ,
,  ,
,  .
. і радіуса
і радіуса 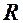 .
. – довільна точка кола.
– довільна точка кола.
 і
і  за формулою відстані між двома точками на площині:
за формулою відстані між двома точками на площині: , звідси маємо
, звідси маємо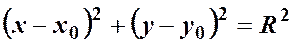 –
–
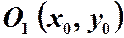 радіуса
радіуса  .
.
 .
.
 і
і  рівні;
рівні; .
. ,
,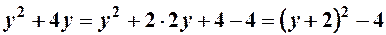 .
. – рівняння кола з центром в точці
– рівняння кола з центром в точці  радіуса
радіуса 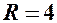 .
. і
і 
 .
. і
і 

 – довільна точка еліпса. За визначенням еліпса маємо:
– довільна точка еліпса. За визначенням еліпса маємо: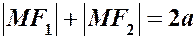 .
. ;
; ,
, ,
, .
. ,
, ,
, ,
,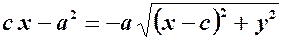 ,
, ,
, .
. , отже
, отже  .
. . Тоді рівняння перепишеться:
. Тоді рівняння перепишеться: , або
, або  – канонічне рівняння еліпса.
– канонічне рівняння еліпса. – велика вісь еліпса,
– велика вісь еліпса,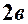 – мала вісь еліпса,
– мала вісь еліпса,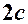 – відстань між фокусами,
– відстань між фокусами,  ,
, – центр еліпса.
– центр еліпса. ;
;  ;
;  ;
; 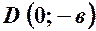 .
.
 .
.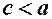 , то
, то  .
. , то еліпс сплющується.
, то еліпс сплющується. від нього. Директриси еліпса
від нього. Директриси еліпса  .
. .
. ,
,  – велика піввісь;
– велика піввісь;  ,
,  – мала піввісь.
– мала піввісь.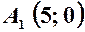 ,
, ;
; ,
, .
. :
: .
. від центра еліпса і мають координати
від центра еліпса і мають координати  ,
,  .
. .
. , звідси
, звідси  .
. і має велику піввісь
і має велику піввісь  .
. .
. .
. .
. .
. (менша, ніж відстань між фокусами).
(менша, ніж відстань між фокусами). і
і 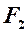 через
через  – довільна точка гіперболи, тоді
– довільна точка гіперболи, тоді 
 .
.
 ,
, і
і .
. – канонічне рівняння гіперболи,
– канонічне рівняння гіперболи, ,
,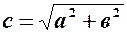 .
. ,
, 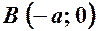 . Точка
. Точка  – центр гіперболи.
– центр гіперболи. .
.
 .
.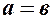 називається р і в н о б і ч н о ю.
називається р і в н о б і ч н о ю. і від даної прямої
і від даної прямої  . Рівняння привести до канонічного виду та побудувати криву.
. Рівняння привести до канонічного виду та побудувати криву.
 .
. і
і  ,
, ,
, ,
, ;
; ;
; ;
; ;
; .
. .
. , уявна піввісь
, уявна піввісь  .
. .
. ,
,  .
. . Рівняння асимптот гіперболи мають вид:
. Рівняння асимптот гіперболи мають вид:  і
і  .
. і
і  – асимптоти.
– асимптоти.


