
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Відстань між двома точками на площиніСодержание книги Поиск на нашем сайте
Нехай задано точки
З
Отже, відстань між двома точками на площині
Відстань точки
ДІЛЕННЯ ВІДРІЗКА В ЗАДАНОМУ ВІДНОШЕННІ
Дано точки
Вимагається знайти координати точки
Координати точки
Зауваження. Координати середини відрізка
ПОНЯТТЯ РІВНЯННЯ ЛІНІЇ НА ПЛОЩИНІ
Нехай на площині задано декартову прямокутну систему координат
Означення. Рівняння
РІВНЯННЯ ПРЯМОЇ НА ПЛОЩИНІ
Рівняння прямої з кутовим коефіцієнтом. Означення. Кутом нахилу прямої до осі
Означення. Кутовим коефіцієнтом прямої називається тангенс кута нахилу цієї прямої до осі
Рівняння прямої з кутовим коефіцієнтом має вид:
Числовий параметр
Розглянемо деякі частинні випадки.
1) Якщо
2) Якщо
3) Якщо
Загальне рівняння прямої. Т е о р е м а. Кожне рівняння першого ступеня відносно х і у, тобто рівняння виду
Рівняння
називають загальним рівнянням прямої.
Частинні випадки.
1)
2)
3) 4)
5)
Рівняння прямої, що проходить через задану точку в заданому напрямі. Нехай задано точку
називають рівнянням прямої, що проходить через задану точку в заданому напрямі.
Рівняння прямої, що проходить через дві задані точки. Нехай задано точки
Використаємо рівняння (3). Підставимо в це рівняння координати точки Маємо
Підставимо цей кутовий коефіцієнт в рівняння (3).
Дістанемо
звідки
рівняння прямої, що проходить через дві задані точки.
В рівнянні (4) припускаємо, що
Якщо
Якщо
Рівняння прямої у відрізках на осях. Рівняння прямої у відрізках на осях має вид:
Параметр
КУТ МІЖ ДВОМА ПРЯМИМИ. УМОВА ПАРАЛЕЛЬНОСТІ ТА ПЕРПЕНДИКУЛЯРНОСТІ ПРЯМИХ
Нехай задано дві прямі, що перетинаються:
Під кутом між двома прямими розуміємо найменший кут
тоді
З урахуванням
тангенс кута між двома прямими. Якщо прямі паралельні, то
Умова п а р а л е л ь н о с т і двох прямих. Дві пряміпаралельні тоді і лише тоді, коли їх кутові коефіцієнти рівні:
Якщо дві прямі перпендикулярні, то формула (6) не має змісту. Але в цьому випадку можна розглянути котангенс кута між прямими
Для перпендикулярних прямих
Умова п е р п е н д и к у л я р н о с т і двох прямих.
Дві прямі на площині перпендикулярні тоді і тільки тоді, коли їх кутові коефіцієнти обернені за величиною і протилежні за знаком:
ТОЧКА ПЕРЕТИНУ ДВОХ ПРЯМИХ
Нехай задано дві прямі:
Вимагається знайти координати точки перетину цих прямих.
Оскільки точка перетину прямих лежить як на першій, так і на другій прямій, то координати цієї точки повинні задовольняти кожне з рівнянь прямих. Отже, для того, щоб знайти координати точки перетину прямих, треба розв’язати сумісно систему рівнянь цих прямих:
Зауваження. 1. Якщо
2. Якщо
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 597; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.57.173 (0.008 с.) |

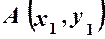 і
і  . Визначимо відстань між ними.
. Визначимо відстань між ними.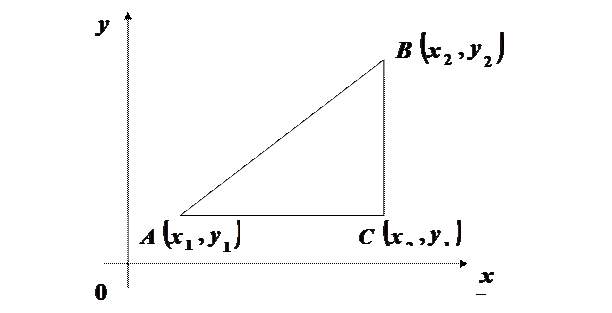
 маємо:
маємо: .
.
 від початку координат знаходимо за формулою
від початку координат знаходимо за формулою  .
.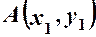 та
та  .
. , яка ділить відрізок
, яка ділить відрізок  у відношенні
у відношенні  , тобто
, тобто .
. .
. знаходимо за формулами
знаходимо за формулами .
. і деяку лінію
і деяку лінію  .
. називають рівнянням лінії (відносно заданої системи координат), якщо рівняння задовольняється координатами
називають рівнянням лінії (відносно заданої системи координат), якщо рівняння задовольняється координатами  і
і  будь-якої точки, яка лежить на лінії і не задовольняється координатами
будь-якої точки, яка лежить на лінії і не задовольняється координатами  називається кут між прямою та віссю
називається кут між прямою та віссю  .
.


 називають початковою ординатою. Параметр
називають початковою ординатою. Параметр  , то рівняння (1) має вигляд
, то рівняння (1) має вигляд  – рівняння прямої, що проходить через початок системи координат.
– рівняння прямої, що проходить через початок системи координат. , то рівняння (1) має вигляд
, то рівняння (1) має вигляд  – рівняння прямої, паралельної осі
– рівняння прямої, паралельної осі  , то рівняння (1) має вигляд
, то рівняння (1) має вигляд  – рівняння осі
– рівняння осі  , визначає на площині пряму лінію.
, визначає на площині пряму лінію.
 ,
, 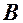 ,
,  .
.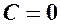 ,
,  . Рівняння (2) тоді матимемо вид
. Рівняння (2) тоді матимемо вид  – рівняння прямої, що проходить через початок системи координат.
– рівняння прямої, що проходить через початок системи координат. ,
,  . Пряма визначається рівнянням
. Пряма визначається рівнянням  , або
, або  – пряма, яка паралельна осі
– пряма, яка паралельна осі  ,
,  . В цьому випадку рівняння (2) буде мати вид
. В цьому випадку рівняння (2) буде мати вид  , звідки
, звідки  – рівняння прямої, паралельної осі
– рівняння прямої, паралельної осі  .
. ,
,  , рівняння (2) має вигляд:
, рівняння (2) має вигляд: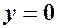 – рівняння осі
– рівняння осі 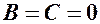 ,
,  , рівняння (2) має вигляд:
, рівняння (2) має вигляд: – рівняння осі
– рівняння осі 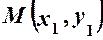 , через яку проходить пряма і кутовий коефіцієнт
, через яку проходить пряма і кутовий коефіцієнт  цієї прямої, тоді рівняння
цієї прямої, тоді рівняння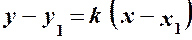
 і
і  . Вимагається скласти рівняння прямої, що проходить через ці точки.
. Вимагається скласти рівняння прямої, що проходить через ці точки. .
.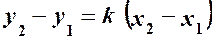 , звідки
, звідки  – кутовий коефіцієнт прямої, яка проходить через дві задані точки.
– кутовий коефіцієнт прямої, яка проходить через дві задані точки. ,
,
 ,
,  , інакше, це рівняння не має змісту.
, інакше, це рівняння не має змісту. , то будемо мати
, то будемо мати  – пряма, паралельна осі ординат.
– пряма, паралельна осі ординат. , то маємо пряму
, то маємо пряму  – пряма паралельна осі абсцис.
– пряма паралельна осі абсцис.

 в цьому рівнянні – абсциса точки перетину прямої з віссю
в цьому рівнянні – абсциса точки перетину прямої з віссю  і
і  . Вимагається знайти кут між цими прямими.
. Вимагається знайти кут між цими прямими.
 , утворений цими прямими, який відраховуємо проти годинникової стрілки.
, утворений цими прямими, який відраховуємо проти годинникової стрілки. , звідки
, звідки  ,
, .
. ,
,  остаточно маємо:
остаточно маємо: –
–
 , а отже
, а отже  .
. .
. , отже
, отже  , звідки
, звідки  .
. .
.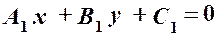 і
і 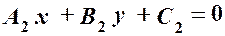 .
.
 , то прямі паралельні, точок перетину немає.
, то прямі паралельні, точок перетину немає. , то прямі зливаються, і таким чином точок перетину безліч.
, то прямі зливаються, і таким чином точок перетину безліч.


