
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття кривої другого порядкуСодержание книги Поиск на нашем сайте
Означення. Кривою другого порядку називають лінію, що визначається рівнянням другого степеня відносно декартових координат:
де
КОЛО
Означення. Коло – геометричне місце точок площини, рівновіддалених від даної точки, що називається центром кола.
Одержимо рівняння кола з центром в точці
Нехай точка
Визначимо відстань між точками
канонічне рівняння кола з центром в точці
Коло радіуса
Якщо в рівнянні (1) розкрити дужки, то одержимо рівняння кола у вигляді:
Як бачимо, для рівняння кола виконуються дві умови: 1) коефіцієнти при 2) відсутній член з добутком координат х ∙ у. Приклад 2. Знайти центр і радіус кола Розв’язання.
Перетворимо ліву частину рівняння, виділимо для цього повні квадрати по змінним
ЕЛІПС
Означення. Еліпсом називається геометричне місце точок площини, сума відстаней від кожної з яких до двох заданих точок (фокусів), є величина стала, дорівнює 2а, більша, ніж відстань між фокусами.
Позначимо відстань між фокусами Виберемо систему координат так, щоб фокуси мали координати
Нехай точка
тоді
Ліву і праву частини останнього рівняння піднесемо до квадрату:
звідки
або
тоді
Згідно з умовою в означенні еліпса
Позначимо
Еліпс, заданий канонічним рівнянням, симетричний відносно осей координат:
точка
Точки перетину еліпса з осями називаються вершинами еліпса.
Отже, еліпс має чотири вершини:
Означення. Ексцентриситетом еліпса називається відношення відстані між фокусами до довжини великої осі.
Оскільки
Ексцентриситет характеризує форму еліпса: якщо
Означення. Директрисами еліпса називають дві прямі, перпендикулярні до фокальної осі еліпса і розміщенні симетрично відносно центра еліпса на відстані
Приклад 3. Побудувати, виписати основні числові характеристики:
Розв’язання. Дане рівняння є канонічним рівнянням еліпса.
Побудуємо прямокутну декартову систему координат на площині. Вздовж осі

Вершини еліпса мають координати:
Визначимо параметр
Фокуси лежать на осі
Ексцентриситет еліпса
Директриси мають рівняння:
Приклад 4.
Скласти канонічне рівняння еліпса, що проходить через точку
Розв’язання.
Канонічне рівняння еліпса має вид:
З урахуванням, що велика піввісь
Оскільки точка Визначимо звідси:
Тепер запишемо шукане канонічне рівняння еліпса:
ГІПЕРБОЛА
Означення. Гіперболою називається геометричне місце точок на площині, абсолютна величина різниці відстаней яких до двох заданих точок – фокусів, є величина стала, дорівнює
Позначимо відстань між фокусами
Нехай точка
Зробивши перетворення, аналогічні тим, що зроблено при виведенні рівняння еліпса маємо:
де
Гіпербола має дві вершини:
Означення. Ексцентриситетом гіперболи називається відношення відстані між фокусами до довжини дійсної осі:
Означення. Асимптотою кривої називають таку пряму з властивістю, що точка, яка віддаляється по кривій у нескінченність, необмежено наближається до цієї прямої.
Гіпербола має дві асимптоти:
Означення. Директрисами гіперболи називаються дві прямі, перпендикулярні до фокусної (дійсної) осі гіперболи і знаходяться на відстані
Означення. Гіпербола, у якої Приклад 5.
Скласти рівняння геометричного місця точок, відношення відстаней яких від даної точки Розв’язання.
В прямокутній декартовій системі координат побудуємо точку
 – довільна точка шуканого геометричного місця точок. – довільна точка шуканого геометричного місця точок.  – перпендикуляр до прямої – перпендикуляр до прямої  . Точка . Точка 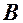 має координати має координати  . .
За умовою задачі
Відстані
тепер маємо:
Ліву і праву частини рівняння розділимо почленно на 5:
Одержане рівняння – канонічне рівняння гіперболи. Дійсна піввісь
Визначимо координати фокусів гіперболи:
Отже, фокуси гіперболи: Ексцентриситет одержаної гіперболи Отже, Директриса гіперболи: Для даного приклада:
Зробимо рисунок.

ПАРАБОЛА
Означення. Парабола – геометричне місце точок площини рівновіддалених від даної точки – фокуса і від даної прямої, яка називається директрисою.
Нехай точка
Декартову прямокутну систему координат вибираємо так, щоб вісь Позначимо відстань від заданої точки
Тоді координати фокуса
отже, Рівняння
Ексцентриситет параболи дорівнює одиниці: Приклад 6. Дана парабола
Розв’язання. Проаналізуємо задане рівняння.
Отже, рівняння директриси
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 709; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.24.49 (0.01 с.) |

 ,
, ,
,  ,
,  ,
,  ,
,  – дійсні числа і
– дійсні числа і  і радіуса
і радіуса 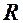 .
. – довільна точка кола.
– довільна точка кола.
 і
і  за формулою відстані між двома точками на площині:
за формулою відстані між двома точками на площині: , звідси маємо
, звідси маємо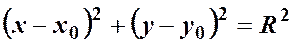 –
–
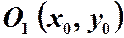 радіуса
радіуса  .
.
 .
.
 і
і  рівні;
рівні; .
. і
і  .
. ,
,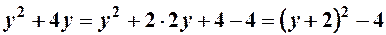 .
. – рівняння кола з центром в точці
– рівняння кола з центром в точці  радіуса
радіуса 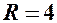 .
. і
і 
 .
. і
і 

 – довільна точка еліпса. За визначенням еліпса маємо:
– довільна точка еліпса. За визначенням еліпса маємо: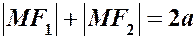 .
. ;
; ,
, ,
, .
. ,
, ,
, ,
,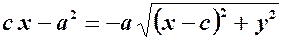 ,
, ,
, .
. , отже
, отже  .
. . Тоді рівняння перепишеться:
. Тоді рівняння перепишеться: , або
, або  – канонічне рівняння еліпса.
– канонічне рівняння еліпса. – велика вісь еліпса,
– велика вісь еліпса,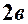 – мала вісь еліпса,
– мала вісь еліпса,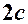 – відстань між фокусами,
– відстань між фокусами,  ,
, – центр еліпса.
– центр еліпса. ;
;  ;
;  ;
; 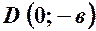 .
.
 .
.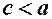 , то
, то  .
. , то еліпс сплющується.
, то еліпс сплющується. від нього. Директриси еліпса
від нього. Директриси еліпса  .
. .
. ,
,  – велика піввісь;
– велика піввісь;  ,
,  – мала піввісь.
– мала піввісь. вліво і вправо від початку системи координат відкладемо відстань
вліво і вправо від початку системи координат відкладемо відстань  вгору і вниз – відстань
вгору і вниз – відстань 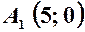 ,
, ;
; ,
, .
. :
: .
. від центра еліпса і мають координати
від центра еліпса і мають координати  ,
,  .
. .
. , звідси
, звідси  .
. і має велику піввісь
і має велику піввісь  .
. .
. .
. .
. .
. (менша, ніж відстань між фокусами).
(менша, ніж відстань між фокусами). і
і 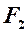 через
через  – довільна точка гіперболи, тоді
– довільна точка гіперболи, тоді 
 .
.
 ,
, і
і .
. – канонічне рівняння гіперболи,
– канонічне рівняння гіперболи, ,
,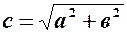 .
. ,
, 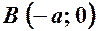 . Точка
. Точка  – центр гіперболи.
– центр гіперболи. .
.
 .
.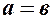 називається р і в н о б і ч н о ю.
називається р і в н о б і ч н о ю. і від даної прямої
і від даної прямої  . Рівняння привести до канонічного виду та побудувати криву.
. Рівняння привести до канонічного виду та побудувати криву.
 .
. і
і  ,
, ,
, ,
, ;
; ;
; ;
; ;
; .
. .
. , уявна піввісь
, уявна піввісь  .
. .
. ,
,  .
. . Рівняння асимптот гіперболи мають вид:
. Рівняння асимптот гіперболи мають вид:  і
і  .
. і
і  – асимптоти.
– асимптоти. і
і  – рівняння директрис.
– рівняння директрис.

 – фокус параболи, а пряма
– фокус параболи, а пряма  – її директриса.
– її директриса. .
.
 , рівняння директриси
, рівняння директриси  . Нехай
. Нехай  .
. ,
, ,
, ,
,  ,
, – канонічне рівняння параболи,
– канонічне рівняння параболи,  – параметр параболи (відстань від фокуса до директриси). Вершина параболи ділить відстань між фокусом і директрисою навпіл.
– параметр параболи (відстань від фокуса до директриси). Вершина параболи ділить відстань між фокусом і директрисою навпіл. ,
,  ,
,  – канонічні рівняння параболи.
– канонічні рівняння параболи.


 .
. . Записати рівняння директриси і знайти координати фокуса.
. Записати рівняння директриси і знайти координати фокуса. , звідки
, звідки 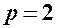 .
. , а фокус має координати
, а фокус має координати  .
.


