
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналітична геометрія у просторіСодержание книги Поиск на нашем сайте
РІВНЯННЯ ПЛОЩИНИ, ЩО ПРОХОДИТЬ ЧЕРЕЗ ЗАДАНУ ТОЧКУ ПЕРПЕНДИКУЛЯРНО ДО ЗАДАНОГО ВЕКТОРА
Нехай площину
Вектор
Візьмемо на площині
При будь-якому положенні точки
або
рівняння площини, що проходить через задану точку ЗАГАЛЬНЕ РІВНЯННЯ ПЛОЩИНИ. ДОСЛІДЖЕННЯ НЕПОВНОГО РІВНЯННЯ ПЛОЩИНИ Якщо в останньому рівнянні відкрити дужки, то одержимо Позначимо – будемо мати
Як бачимо, це рівняння першого степеня відносно
Рівняння площини називають неповним, якщо в ньому відсутні деякі члени.
1. Якщо в рівнянні площини вільний член
2. Якщо в рівнянні
Аналогічно,
3. Якщо в рівнянні площини
Аналогічно,
4. Якщо в рівнянні площини
Аналогічно,
5. Якщо в рівнянні площини
Аналогічно,
КУТ МІЖ ДВОМА ПЛОЩИНАМИ. УМОВИ ПАРАЛЕЛЬНОСТІ ТА ПЕРПЕНДИКУЛЯРНОСТІ ПЛОЩИН
Нехай задано дві площини:
з нормальними векторами
Тоді кут між площинами – це кут між векторами
Звідси одержуємо:
Умова паралельності площин:
Умова перпендикулярності площин:
ВІДСТАНЬ ВІД ТОЧКИ ДО ПЛОЩИНИ
Відстанню від заданої точки
Нехай точка
РІВНЯННЯ ПРЯМОЇ У ПРОСТОРІ
Пряму
Вектор
Пряма має безліч напрямних векторів. Всі вони паралельні між собою, а отже, їх координати пропорційні.
Нехай точка
Якщо кожне з відношень прирівняємо до параметра
Пряму у просторі можна задати як перетин двох площин, тобто системою двох лінійних рівнянь:
Для того, щоб дві площини визначили пряму, треба щоб вони не були паралельні, тобто вектори
Якщо пряма
КУТ МІЖ ДВОМА ПРЯМИМИ
Кут
Нехай
Умова паралельності двох прямих у просторі:
Умова перпендикулярності двох прямих у просторі:
ПЕРЕТИН ПРЯМОЇ З ПЛОЩИНОЮ
Нехай задано площину
Вимагається знайти точку перетину прямої з площиною. Для цього розв’яжемо систему рівнянь
Запишемо параметричні рівняння прямої:
звідки
Можливі наступні випадки:
1.
2.
3.
Приклад 9. Знайти точку перетину прямої
Розв’язання.
Для того, щоб знайти координати точки перетину прямої з площиною, розв’яжемо систему
Запишемо параметричні рівняння прямої. Для цього кожне з відношень прирівняємо до параметра
Параметричні рівняння прямої підставляємо тепер в рівняння площини:
Тепер маємо:
РОЗДІЛ 5. СФЕРА
Означення. Сфера – геометричне місце точок площини, рівновіддалених від даної точки – центра сфери.
Канонічне рівняння сфери має вид:
де
Рівняння другого степеня відносно
1. це рівняння ІІ степеня відносно
2. коефіцієнти при квадратах
3. в рівнянні немає членів з добутками
Приклад 10.
Дано рівняння
Потрібно:
1) довести, що дане рівняння є рівнянням сфери; 2) знайти координати центра і радіус сфери; 3) скласти рівняння площини, що проходить через центр сфери і вісь 4) скласти рівняння прямої, що проходить через центр сфери і початок координат;
Розв’язання.
1) Дане рівняння є рівнянням сфери, оскільки це рівняння другого степеня відносно
2) Визначимо координати центра і радіус сфери. Для цього виділимо повні квадрати по змінним
3) Одержимо тепер рівняння площини, що проходить через точку
Оскільки площина проходить через вісь З іншого боку, оскільки шукана площина проходить через центр сфери – точку
Один із параметрів
4) Для того, щоб одержати рівняння прямої, що проходить через центр сфери і початок координат скористуємось рівнянням прямої, що проходить через дві задані точки:
Точка
Питання для самоперевірки
1. Який вид має рівняння площини, що проходить:
а) через задану точку перпендикулярно до заданого вектора;
б) загальне рівняння площини?
2. Дослідження неповного рівняння площини.
3. Як знайти кут між двома площинами? Сформулюйте умови паралельності та перпендикулярності площин.
4. Як знайти відстань від заданої точки до заданої площини?
5. Які Ви знаєте види рівнянь прямої у просторі.
6. Яка умова паралельності прямих у просторі? Сформулюйте також умову перпендикулярності прямих у просторі.
7. Як знайти координати точки перетину площини і прямої?
8. Як знайти відстань від заданої точки до заданої площини?
9. За яких умов загальне рівняння другого степеня визначає сферу? Як знайти її центр та радіус? Задачі до розділів 4, 5
В задачах 1–20 дано рівняння
Потрібно:
1) довести, що рівняння
2) знайти координати центра і радіус сфери;
3) скласти рівняння площини, що проходить через центр сфери і задану вісь;
4) скласти рівняння прямої, що проходить через центр сфери і задану точку
121.
122.
123.
124.
125.
126.
127.
128.
129.
130.
131.
132.
133.
134.
135.
136.
137.
138.
139.
140.
БІБЛІОГРАФІЧНИЙ СПИСОК
1. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М.: Наука, 1986.
2. Шнейдер В.Е., Слуцкий А.И., Шумов А.С. Краткий курс высшей математики. М.: Высшая школа, 1972.
3. Шкіль М.І., Колесник Т.В., Котлова В.М. Вища математика. Київ: „Либідь”, 1994, книга 1.
4. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах. М.: Высшая школа, 1974, часть 1.
5. Минорский В.П. Сборник задач по высшей математике. М.: Наука, 1987.
6. Дубовик В.П., Юрик І.І. Вища математика. Київ: Вища школа, 1993.
7. Лихолетов И.И., Мацкевич И.П. Руководство к решению задач по высшей математике, теории вероятностей и математической статистике. Минск: Высшая школа, 1969. ЗМІСТ
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 941; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.174.45 (0.008 с.) |

 у просторі задано деякою її точкою
у просторі задано деякою її точкою  та ненульовим вектором
та ненульовим вектором 
 , перпендикулярним цій площині.
, перпендикулярним цій площині. називають нормальним вектором площини.
називають нормальним вектором площини. довільну точку
довільну точку  . Тоді вектор
. Тоді вектор  має координати
має координати  .
. на площині
на площині  , а отже, їх скалярний добуток буде дорівнювати 0:
, а отже, їх скалярний добуток буде дорівнювати 0: ,
, –
– перпендикулярно вектору
перпендикулярно вектору  .
.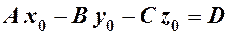 ,
, – загальне рівняння площини.
– загальне рівняння площини.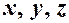 ; вектор
; вектор 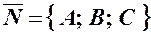 – нормальний вектор площини.
– нормальний вектор площини. , то площина проходить через початок системи координат.
, то площина проходить через початок системи координат. , то площина
, то площина  паралельна осі
паралельна осі  .
. – площина паралельна осі
– площина паралельна осі  ,
,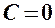 – площина паралельна осі
– площина паралельна осі  .
. , то площина
, то площина  паралельна координатній площині
паралельна координатній площині  .
. – площина паралельна осі
– площина паралельна осі  ,
, – площина паралельна осі
– площина паралельна осі  .
. , то площина
, то площина  проходить через вісь
проходить через вісь  – площина проходить через вісь
– площина проходить через вісь  – площина проходить через вісь
– площина проходить через вісь 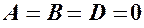 , то площина
, то площина  , або
, або  – площина
– площина  – площина
– площина  – площина
– площина  і
і 
 ,
, .
. і
і  .
. .
. ;
; .
. до площини
до площини  називають довжину перпендикуляра, опущеного із точки
називають довжину перпендикуляра, опущеного із точки  , а площина
, а площина  , тоді відстань від точки
, тоді відстань від точки  .
. у просторі в прямокутній декартовій системі координат можна задати точкою
у просторі в прямокутній декартовій системі координат можна задати точкою 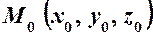 і вектором
і вектором  , паралельним цій прямій.
, паралельним цій прямій. називають напрямним вектором прямої.
називають напрямним вектором прямої. – поточна точка прямої
– поточна точка прямої  колінеарний вектору
колінеарний вектору  – канонічні рівняння прямої, що проходить через точку
– канонічні рівняння прямої, що проходить через точку  паралельно вектору
паралельно вектору  , тобто
, тобто  ,
,  ,
,  і виразимо координати поточної точки
і виразимо координати поточної точки  через
через  ,
,  ,
,  – параметричні рівняння прямої.
– параметричні рівняння прямої. .
. і
і  не паралельні (це означає, що їх координати не пропорційні).
не паралельні (це означає, що їх координати не пропорційні). і
і 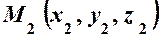 , то
, то  – канонічні рівняння прямої, що проходить через дві задані точки.
– канонічні рівняння прямої, що проходить через дві задані точки. між двома прямими
між двома прямими 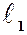 і
і  – це кут між їхніми напрямними векторами
– це кут між їхніми напрямними векторами  і
і  .
. ,
,  , тоді
, тоді .
.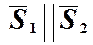 , отже їх координати пропорційні:
, отже їх координати пропорційні: .
. , отже
, отже .
. і пряму
і пряму  .
.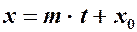 ,
, 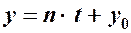 ,
,  і підставимо їх в рівняння площини:
і підставимо їх в рівняння площини: ,
, ,
,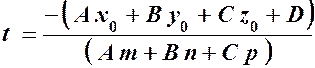 .
. – тоді система має єдиний розв’язок (пряма і площина перетинаються в одній точці);
– тоді система має єдиний розв’язок (пряма і площина перетинаються в одній точці); ,
,  – система розв’язків не має (пряма паралельна площині);
– система розв’язків не має (пряма паралельна площині); – система має безліч розв’язків (пряма належить площині).
– система має безліч розв’язків (пряма належить площині). з площиною
з площиною  .
.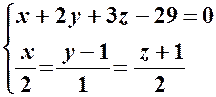 .
. :
: ;
;  .
.
 ,
, ,
, ,
, .
. ,
,  ,
,  – координати точки перетину прямої і площини.
– координати точки перетину прямої і площини. ,
, – координати центра сфери,
– координати центра сфери,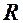 – радіус.
– радіус. тоді і лише тоді буде рівняння сфери, коли:
тоді і лише тоді буде рівняння сфери, коли: .
. .
. ;
; .
.
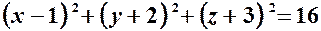 – канонічне рівняння сфери з центром в точці
– канонічне рівняння сфери з центром в точці  радіуса
радіуса  .
.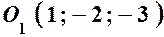 і вісь
і вісь  і рівняння площини має вид
і рівняння площини має вид 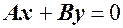 .
. , то координати цієї точки повинні задовольняти рівнянню площини.
, то координати цієї точки повинні задовольняти рівнянню площини. ,
, .
. або
або 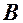 можна вибрати довільно, але
можна вибрати довільно, але  . Нехай
. Нехай  , тоді
, тоді  .
. – рівняння шуканої площини.
– рівняння шуканої площини. .
. , тоді
, тоді ;
; – рівняння прямої
– рівняння прямої 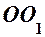 .
. .
. , вісь
, вісь  .
. , вісь
, вісь  ,
,  .
. , вісь
, вісь  .
. , вісь
, вісь  ,
,  .
. , вісь
, вісь  .
. , вісь
, вісь 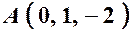 .
. , вісь
, вісь  .
. , вісь
, вісь  .
. , вісь
, вісь  .
. , вісь
, вісь  .
. , вісь
, вісь 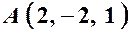 .
. , вісь
, вісь  .
. , вісь
, вісь  .
. , вісь
, вісь  .
. , вісь
, вісь  .
. , вісь
, вісь  .
. , вісь
, вісь  .
.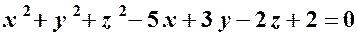 , вісь
, вісь  .
. , вісь
, вісь 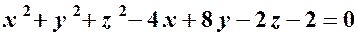 , вісь
, вісь  .
.


