
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перетворення декартових координатСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Паралельне перенесення системи координат
Систему координат
Дістанемо систему координат
Поворот системи координат на кут φ Нехай задана прямокутна декартова система координат
Тоді залежність між старими координатами
ПОБУДОВА КРИВИХ ДРУГОГО ПОРЯДКУ ЗА ЇХ РІВНЯННЯМ
Вид рівняння кривої залежить від вибору системи координат. В різних системах координат для однієї й тієї ж кривої ми будемо одержувати рівняння різної складності. Отже, виникає наступна задача. Дано рівняння кривої другого порядку в деякій декартовій системі координат
Розглянемо рівняння другого степеня виду
Таке рівняння визначає на площині еліпс, гіперболу або параболу (можливі випадки виродження цих кривих). Для того, щоб привести це рівняння до канонічного виду треба виділити повні квадрати по змінним х і у і виконати паралельне перенесення системи координат.
При цьому, якщо:
1)
2)
3)
ГРАФІК КВАДРАТНОГО ТРИЧЛЕНА
Нехай задано рівняння виду
Графіком квадратного тричлена є парабола з віссю симетрії, паралельній осі ординат. Якщо параметр
Аналогічно, рівняння
Ці рівняння паралельним перенесенням системи координат перетворюються до канонічного виду рівняння параболи.
Приклад 7.
Привести до канонічного виду рівняння
Розв’язання. Виділимо повний квадрат по змінній
Тепер маємо
Виконаємо паралельне перенесення системи координат:
В новій системі координат

ГРАФІК ОБЕРНЕНО ПРОПОРЦІЙНОЇ ЗАЛЕЖНОСТІ
Розглянемо функцію
Для того, щоб привести дане рівняння до канонічного виду, труба виконати поворот осей координат на кут При
Старі осі
Питання для самоперевірки
1. Що називається кривою другого порядку?
2. Дайте означення кола. Яке канонічне рівняння кола? Який вид має рівняння кола з центром в початку координат?
3. Що називається еліпсом? Яке канонічне рівняння еліпса?
4. Що називається ексцентриситетом еліпса? Як змінюється форма еліпса, якщо ексцентриситет зменшується, наближаючись до нуля; або збільшується, наближаючись до одиниці?
5. Дайте означення гіперболи. Яке канонічне рівняння гіперболи? Що називається ексцентриситетом гіперболи?
6. Які прямі називаються асимптотами гіперболи? Який вид мають рівняння асимптот гіперболи, заданої канонічним рівнянням?
7. Яка гіпербола називається рівнобічною?
8. Що називається параболою? Який вид має канонічне рівняння параболи, симетричної відносно осі
9. Що називається директрисами еліпса, гіперболи?
10. Який вид мають формули перетворення прямокутних координат при паралельному перенесенні системи координат? При повороті системі координат на кут
11. Що являється графіком квадратного тричлена?
12. Обернено пропорційна залежність. Що являється її графіком?
Задачі до розділу 2
41. Знайти координати центра і радіус кола
42. Дані точки
43. Привести до канонічного виду рівняння
44. Знайти відстань між центрами двох кіл:
45. Скласти рівняння кола, яке проходить через точки
46. Скласти канонічне рівняння еліпса, якщо відстань між фокусами дорівнює 16, а ексцентриситет
47. Побудувати, виписати основні числові характеристики:
48. Записати рівняння еліпса, фокуси якого лежать на осі абсцис симетрично початку координат, якщо велика піввісь дорівнює 13, а відстань між фокусами – 10.
49. Записати рівняння еліпса, що проходить через точки
50. Еліпс, симетричний відносно осей координат, фокуси якого розташовані на осі
51. Записати канонічне рівняння гіперболи, яка проходить через точку 52. Фокуси гіперболи співпадають з фокусами еліпса
53. Ексцентриситет гіперболи дорівнює
54. Побудувати, виписати основні числові характеристики:
55. Записати рівняння гіперболи, фокуси якої лежать на осі
56. Записати рівняння параболи, фокус якої знаходиться в точці
57. Скласти рівняння параболи, вершина якої знаходиться в початку координат, якщо ця парабола проходить через точку
58. Визначити координати фокусів і рівняння директрис для парабол: 1) 2) 3) 4)
59. Знайти відстань від точки
60. Написати рівняння параболи, що проходить через точки
В задачах 61–80 потрібно привести рівняння параболи до канонічного виду, побудувати їх.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
В задачах 81–100 потрібно скласти рівняння геометричного місця точок, відношення відстаней яких до даної точки
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
97.
98.
99.
100.
РОЗДІЛ 3. ЕЛЕМЕНТИ ВЕКТОРНОЇ АЛГЕБРИ ОСНОВНІ ПОНЯТТЯ
Означення. Вектором називають напрямлений відрізок
Геометрично вектор зображують напрямленим відрізком простору.
Означення. Модулем вектора називається довжина відрізка, який зображує вектор і позначається Означення. Два вектори називаються колінеарними, якщо вони розташовані на одній або на паралельних прямих.
Означення. Два вектори називають рівними, якщо вони колінеарні, напрямлені в одну сторону і мають рівні модулі.
Означення. Вектори називають компланарними, якщо вони розташовані в одній або паралельних площинах.
Означення. Нульовим вектором
Модуль нульового вектора дорівнює нулю, а напрям – невизначений.
|
||||||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 1380; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.006 с.) |

 перенесемо паралельно собі так, щоб початок координат співпадав з точкою
перенесемо паралельно собі так, щоб початок координат співпадав з точкою  .
.
 . Координати довільної точки
. Координати довільної точки  в системі
в системі  , а в системі
, а в системі  .
. – формули, які пов’язують координати точки
– формули, які пов’язують координати точки  (початок системи координат не змінюється; кут
(початок системи координат не змінюється; кут  .
.
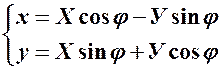 .
. , яке не є простішим. Потрібно за допомогою перетворень координат одержати простіше рівняння кривої.
, яке не є простішим. Потрібно за допомогою перетворень координат одержати простіше рівняння кривої. (це рівняння не містить члена
(це рівняння не містить члена  з добутком координат).
з добутком координат). , маємо рівняння еліпса (
, маємо рівняння еліпса ( – рівняння кола);
– рівняння кола); , маємо рівняння гіперболи;
, маємо рівняння гіперболи; , маємо рівняння параболи.
, маємо рівняння параболи. , права частина якого – квадратний тричлен.
, права частина якого – квадратний тричлен. , то вітки параболи напрямлені вгору, при
, то вітки параболи напрямлені вгору, при  – вниз.
– вниз. визначає параболу, вісь симетрії якої паралельна осі
визначає параболу, вісь симетрії якої паралельна осі  .
. , побудувати параболу.
, побудувати параболу. .
.
 .
. , або
, або 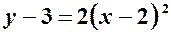 .
.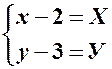 ,
, ,
, – центр нової системи координат.
– центр нової системи координат. – канонічне рівняння параболи з вершиною в точці
– канонічне рівняння параболи з вершиною в точці 

 . Графіком цієї функції є рівнобічна гіпербола, асимптоти якої співпадають з координатними осями.
. Графіком цієї функції є рівнобічна гіпербола, асимптоти якої співпадають з координатними осями. .
. гілки гіперболи розташовані і І та ІІІ чверті, а її дійсна піввісь співпадає з віссю
гілки гіперболи розташовані і І та ІІІ чверті, а її дійсна піввісь співпадає з віссю  ; при
; при  – гіпербола розташована в ІІ та ІV координатних кутах, дійсна піввісь співпадає з віссю
– гіпербола розташована в ІІ та ІV координатних кутах, дійсна піввісь співпадає з віссю 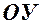 .
. є бісектрисами координатних кутів нової системи
є бісектрисами координатних кутів нової системи  і асимптотами рівнобічної гіперболи.
і асимптотами рівнобічної гіперболи.
 .
. ;
;  . Написати рівняння кола, діаметром якого є відрізок
. Написати рівняння кола, діаметром якого є відрізок  .
. .
.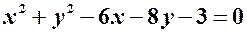 і
і  .
. ,
,  ,
,  .
. .
. .
. ,
, 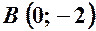 і центр якого співпадає з початком координат, а осями симетрії є осі координат.
і центр якого співпадає з початком координат, а осями симетрії є осі координат. і має ексцентриситет
і має ексцентриситет  . Написати рівняння цього еліпса.
. Написати рівняння цього еліпса. і має асимптоти
і має асимптоти  .
.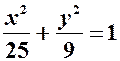 . Скласти канонічне рівняння гіперболи, якщо її ексцентриситет
. Скласти канонічне рівняння гіперболи, якщо її ексцентриситет  .
. . Скласти канонічне рівняння гіперболи, що проходить через точку
. Скласти канонічне рівняння гіперболи, що проходить через точку  .
. .
. , а ексцентриситет
, а ексцентриситет  .
.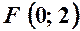 , а рівняння директриси
, а рівняння директриси  .
. і симетрична відносно осі
і симетрична відносно осі  ;
; ;
; ;
; .
. до її вершини, якщо абсциса точки
до її вершини, якщо абсциса точки  і
і  і симетрична відносно осі
і симетрична відносно осі  .
. .
. .
.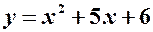 .
. .
. .
. .
. .
. .
.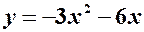 .
. .
. .
.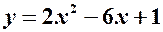 .
. .
. .
. .
. .
. .
. .
.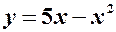 .
. і до даної прямої
і до даної прямої  (або
(або  ) дорівнює числу
) дорівнює числу  . Одержане рівняння привести до канонічного виду і побудувати криву.
. Одержане рівняння привести до канонічного виду і побудувати криву. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  ,
, 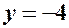 ,
,  ,
,  ,
,  .
. ,
,  ,
,  .
.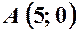 ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
, 
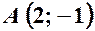 ,
,  ,
,  ,
, 
 ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
.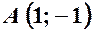 ,
,  ,
,  .
. .
.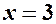 ,
,  , точка
, точка  – початок, а точка
– початок, а точка 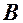 – кінець. Векторна величина характеризується числовим значенням і напрямом.
– кінець. Векторна величина характеризується числовим значенням і напрямом.
 або
або  .
. називається вектор, у якого початок і кінець співпадають.
називається вектор, у якого початок і кінець співпадають.


