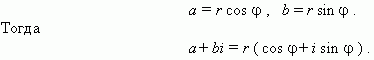Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полярная система координат в плоскостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Луч, выходящий из заданной точки Введем прямоугольную систему координат
Рис. 45 Рис.46 Система уравнений
осуществляет преобразование полярных координат в декартовые (прямоугольные). Правые части в равенствах (1) - непрерывно дифференцируемые функции с якобианом
Уравнение
где Будем считать, что
Рис.47 Зададим в плоскости
Согласно формуле (2) § 2.7 мы заменили Пример 1.
Мы следовали формуле (3). Надо учесть, что область, определяемая в декартовых координатах неравенством Формулу (3) можно получить из естественных соображений, не прибегая к общей формуле (2) § 2.7. Плоскость
где
Пример 2. Вычислить интеграл
Переходя к полярным координатам (рис. 49), получаем
1. Рис. 48 Рис.49 21. Поверхности 2-ого порядка (уравнение и рисунки, самостоятельно конспект). К невырожденным поверхностям второго порядка относятся эллипсоид, эллиптический параболоид, гиперболический параболоид, однополостной гиперболоид и двуполостной гиперболоид. Строгое изучение этих поверхностей проводится в курсе аналитической геометрии. Здесь же мы ограничимся определениями и иллюстрациями.
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
Свойства эллипсоида.
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением Свойства эллиптического параболоида.
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
Свойства гиперболического параболоида.
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
Свойства однополостного гиперболоида.
Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением
Свойства двуполостного гиперболоида.
По аналогии с коническими сечениями существуют и вырожденные поверхности второго порядка. Так, уравнением второго порядка x 2 = 0 описывается пара совпадающих плоскостей, уравнением x 2 = 1 – пара параллельных плоскостей, уравнением x 2 – y 2 = 0 – пара пересекающихся плоскостей. Уравнение x 2 + y 2 + z 2 = 0 описывает точку с координатами (0; 0; 0), уравнение x 2 + y 2 = 1 – круговой цилиндр, уравнение x 2 + y 2 = z 2 – круговой конус. Существуют и другие вырожденные случаи. Полная теория поверхностей второго порядка рассматривается в курсе аналитической геометрии.
вырождающиеся нераспадающиеся поверхности: цилиндрические поверхности, -
конические поверхности -
вырождающиеся распадающиеся поверхности:
21. (К.ч.) Комплексные числа и действия над ними в алгебраической форме (в том числе деление), сопряженное Начальные сведения о мнимых и комплексных числах приведены в разделе «Мнимые и комплексные числа». Необходимость в этих числах нового типа появилась при решении квадратных уравнений для случая D < 0 (здесь D – дискриминант квадратного уравнения). Долгое время эти числа не находили физического применения, поэтому их и назвали «мнимыми» числами. Однако сейчас они очень широко применяются в различных областях физики и техники: электротехнике, гидро- и аэродинамике, теории упругости и др.
Комплексные числа записываются в виде: a+ bi. Здесь a и b – действительные числа, а i – мнимая единица, т.e. i 2 = –1.Число a называется абсциссой, a b – ординатой комплексного числа a+ bi. Два комплексных числа a+ bi и a – bi называются сопряжёнными комплексными числами. Основные договорённости: 1. Действительное число а может быть также записано в форме комплексного числа: a+ 0 i или a – 0 i. Например, записи 5 + 0 i и 5 – 0 i означают одно и то же число 5.
2. Комплексное число 0 + bi называется чисто мнимым числом. Запись bi означает то же самое, что и 0 + bi.
3. Два комплексных числа a+ bi и c+ di считаются равными, если a= c и b= d. В противном случае комплексные числа не равны.
Сложение. Суммой комплексных чисел a+ bi и c+ di называется комплексное число (a+ c) + (b+ d) i. Таким образом, при сложениикомплексных чисел отдельно складываются их абсциссы и ординаты. Это определение соответствует правилам действий с обычными многочленами.
Вычитание. Разностью двух комплексных чисел a+ bi (уменьшаемое) и c+ di (вычитаемое) называется комплексное число (a – c) + (b – d) i. Таким образом, при вычитании двух комплексных чисел отдельно вычитаются их абсциссы и ординаты.
Умножение. Произведением комплексных чисел a+ bi и c+ di называется комплексное число: (ac – bd) + (ad + bc) i. Это определение вытекает из двух требований:
1) числа a+ bi и c+ di должны перемножаться, как алгебраические двучлены, 2) число i обладает основным свойством: i 2 = – 1.
П р и м е р. (a+ bi)(a – bi) = a 2 + b 2. Следовательно, произведение двух сопряжённых комплексных чисел равно действительному положительному числу. Деление. Разделить комплексное число a+ bi (делимое) на другое c+ di (делитель) - значит найти третье число e+ f i (чатное), которое будучи умноженным на делитель c+ di, даёт в результате делимое a+ bi. Если делитель не равен нулю, деление всегда возможно. П р и м е р. Найти (8 + i): (2 – 3 i). Р е ш е н и е. Перепишем это отношение в виде дроби: Умножив её числитель и знаменатель на 2 + 3 i и выполнив все преобразования, получим:
Геометрическое представление комплексных чисел. Действительные числа изображаются точками на числовой прямой:
Здесь точка A означает число –3, точка B – число 2, и O – ноль. В отличие от этого комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a+ bi будет представлено точкой Р с абсциссой а и ординатой b (см. рис.). Эта система координат называется комплексной плоскостью.
Модулем комплексного числа называется длина вектора OP, изображающего комплексное число на координатной (комплексной) плоскости. Модуль комплексного числа a+ bi обозначается | a+ bi | или буквой r и равен:
Сопряжённые комплексные числа имеют одинаковый модуль. __ Аргумент комплексного числа - это угол Тригонометрическая форма комплексного числа. Абсциссу a и ординату b комплексного числа a + bi можно выразить через его модуль r и аргумент
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 830; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.009 с.) |

 , называется полярной осью, а. точку
, называется полярной осью, а. точку  плоскости имеет полярные координаты
плоскости имеет полярные координаты  , где
, где  - расстояние от
- расстояние от  - угол между векторами (направленным отрезком)
- угол между векторами (направленным отрезком)  и полярной осью, отсчитываемый от последней против часовой стрелки.
и полярной осью, отсчитываемый от последней против часовой стрелки. , у которой положительная ось
, у которой положительная ось  совпадает с полярной осью (рис. 46).
совпадает с полярной осью (рис. 46).
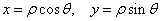 (1)
(1) . (2)
. (2) ,
, - непрерывная на отрезке
- непрерывная на отрезке  функция, определяет в полярных координатах кривую
функция, определяет в полярных координатах кривую  - геометрическое место точек, полярные координаты которых удовлетворяют этому уравнению.
- геометрическое место точек, полярные координаты которых удовлетворяют этому уравнению. . Тогда кривая
. Тогда кривая  пересекает
пересекает 
 , ограниченную лучами
, ограниченную лучами 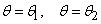 и кривой
и кривой 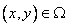 соответствует при помощи уравнений (1) только одной паре
соответствует при помощи уравнений (1) только одной паре  нашей области задана непрерывная функция
нашей области задана непрерывная функция 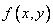 от
от  или она может быть ограниченной на
или она может быть ограниченной на  . (3)
. (3)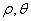 посредством равенства (1) и ввели в качестве множителя абсолютную величину якобиана
посредством равенства (1) и ввели в качестве множителя абсолютную величину якобиана 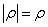 . Для области
. Для области  пар
пар  до
до  .
.
 , в полярных координатах определяется неравенством
, в полярных координатах определяется неравенством  .
.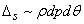 (заштрихованная фигура на рис. 48 может быть приближенно принята за прямоугольник со сторонами
(заштрихованная фигура на рис. 48 может быть приближенно принята за прямоугольник со сторонами 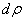 и
и 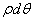 ). Поэтому, если просуммировать по этим элементам, то получим
). Поэтому, если просуммировать по этим элементам, то получим ,
, .
. .
.

 Определение 5.12.
Определение 5.12. a > 0, b > 0, c > 0, называется эллипсоидом.
a > 0, b > 0, c > 0, называется эллипсоидом.




 a > 0, b > 0, называется эллиптическим параболоидом.
a > 0, b > 0, называется эллиптическим параболоидом. a > 0, b > 0, называется гиперболическим параболоидом.
a > 0, b > 0, называется гиперболическим параболоидом.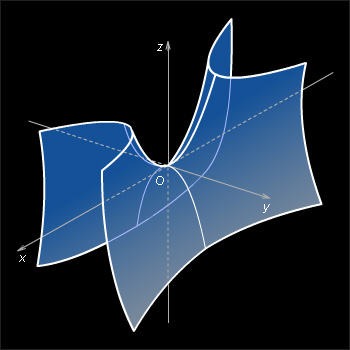
 a > 0, b > 0, c > 0, называется однополостным гиперболоидом.
a > 0, b > 0, c > 0, называется однополостным гиперболоидом.
 a > 0, b > 0, c > 0, называется двуполостным гиперболоидом.
a > 0, b > 0, c > 0, называется двуполостным гиперболоидом.
 и неограничен сверху.
и неограничен сверху. получается эллипс, при
получается эллипс, при  – точка, а в сечении плоскостями, перпендикулярными осям Ox и Oy, – гипербола.
– точка, а в сечении плоскостями, перпендикулярными осям Ox и Oy, – гипербола. - эллипсоид,
- эллипсоид, -мнимый эллипсоид,
-мнимый эллипсоид,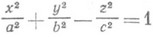 - однополостный гиперболоид,
- однополостный гиперболоид, -двуполостный гиперболоид,
-двуполостный гиперболоид, - эллиптический параболоид,
- эллиптический параболоид, - гиперболический параболоид;
- гиперболический параболоид;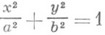 - эллиптический цилиндр,
- эллиптический цилиндр, -мнимый эллиптический цилиндр,
-мнимый эллиптический цилиндр, - гиперболический цилиндр, у 2 = 2рх -параболический цилиндр';
- гиперболический цилиндр, у 2 = 2рх -параболический цилиндр'; - коническая поверхность,
- коническая поверхность, -мнимая коническая поверхность;
-мнимая коническая поверхность;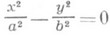 - пара пересекающихся плоскостей,
- пара пересекающихся плоскостей, - пара мнимых пересекающихся плоскостей,
- пара мнимых пересекающихся плоскостей, - пара параллельных плоскостей,
- пара параллельных плоскостей, , модуль z, argz, Argz, свойства аргумента. Тригонометрическая форма К.ч., умножение и деление в тригонометрической форме.
, модуль z, argz, Argz, свойства аргумента. Тригонометрическая форма К.ч., умножение и деление в тригонометрической форме.  . Показательная формула К.ч.
. Показательная формула К.ч.




 между осью OX и вектором OP, изображающим это комплексное число. Отсюда, tan
между осью OX и вектором OP, изображающим это комплексное число. Отсюда, tan  :
: