
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Каноническое уравнение эллипса.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема. В канонической для эллипса системе координат уравнение эллипса имеет вид:
Доказательство. Доказательство проведем в два этапа. На первом этапе мы докажем, что координаты любой точки, лежащей на эллипсе удовлетворяют уравнению (4). На втором этапе мы докажем, что любоерешение уравнения (4) дает координаты точки, лежащей на эллипсе. Отсюда будет следовать, что уравнению (4) удовлетворяют те и только те точки координатной плоскости, которые лежат на эллипсе. Отсюда и изопределения уравнения кривой будет следовать, что уравнение (4) является уравнением эллипса. 1) Пусть точка М(х, у) является точкой эллипса, т.е. сумма ее фокальных радиусов равна 2а:
Воспользуемся формулой расстояния между двумя точками накоординатной плоскости и найдем по этой формуле фокальные радиусы данной точки М:
Перенесем один корень в правую часть равенства и возведем в квадрат:
Сокращая, получаем:
Приводим подобные, сокращаем на 4 и уединяем радикал:
Возводим в квадрат
Раскрываем скобки и сокращаем на
откуда получаем:
Используя равенство (2), получаем:
Разделив последнее равенство на 2) Пусть теперь пара чисел (х, у) удовлетворяет уравнению (4) и пусть М(х, у) – соответствующая точка на координатной плоскости Оху. Тогда из (4) следует:
Подставляем это равенство в выражение для фокальных радиусов точки М:
Здесь мы воспользовались равенством (2) и (3). Таким образом, Теперь заметим, что из равенства (4) следует, что
Отсюда, в свою очередь, следует, что
Из равенств (5) следует, что Теорема доказана. Определение. Уравнение (4) называется каноническим уравнением эллипса. Определение. Канонические для эллипса оси координат называются главными осями эллипса. Определение. Начало канонической для эллипса системы координатназывается центром эллипса.
Определение гиперболы и параболы, уравнение и рисунки. Полярная система координат на плоскости. Гипербола Как учат в школе, графиком функции
Пусть на плоскости даны две точки Определение. Гиперболой называют множество Для того, чтобы получить уравнение гиперболы, воспользуемся методом, который аналогичен тому, что был использован в случае эллипса. Введем систему координат на плоскости так, чтобы фокусы
Пусть точка Перепишем равенство
или
С этим уравнением поступим также, как в случае эллипса мы поступили с уравнением (1):
Произведя необходимые преобразования дальше, получим:
Поделив обе части полученного уравнения на
Осталось доказать, что (2*) - действительно уравнение гиперболы: как и в случае эллипса, мы должны проверить, что если координаты точки Имеем:
Совершенно аналогично
Нам нужно выбрать знак перед скобками так, чтобы каждон из выражений было положительным. Из (2*) замечаем, что Таким образом уравнение (2*) действительно является уравнением гиперболы. Его называют каноническим уравнением гиперболы. Разберемся теперь, как соотносится уравнения (2*) и
и сделаем сначала такую замену переменных:
Тогда уравнение (Ш) примет вид
Это уравнение уже более похоже на уравнение (2*), нам осталось избавиться в нем от суммы
После такой замены (Ш*) примет вид
Парабола В школе говорят, что парабола - это график функции Возьмем точку Определение. Параболой называется множество точек плоскости, равноудаленных от точки Приступим к получению канонического уравнения параболы. Предположим, что расстояние между Пусть точка
После возведения в квадрат этого уравнения, будем иметь
Нам осталось проверить, что всякая точка
|
||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 617; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.98.210 (0.011 с.) |

 . (4)
. (4)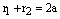 .
. ,
,  , откуда получаем:
, откуда получаем: .
. .
. .
. .
.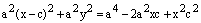 .
.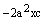 :
: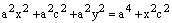 ,
,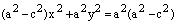 .
.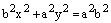 .
.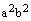 , получаем равенство (4), ч.т.д.
, получаем равенство (4), ч.т.д. .
.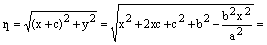
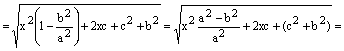
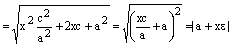 .
.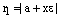 . Аналогично,
. Аналогично, 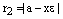 .
.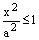 или
или 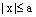 и т.к.
и т.к.  , то отсюда следует неравенство:
, то отсюда следует неравенство: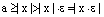 .
. или
или  и
и ,
,  . (5)
. (5) является гипербола. Мы посмотрим на гиперболу несколько с иной точки зрения.
является гипербола. Мы посмотрим на гиперболу несколько с иной точки зрения.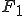 и
и 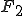 .
.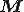 точек плоскости таких, что модуль разности растояний от каждой из таких точек до
точек плоскости таких, что модуль разности растояний от каждой из таких точек до 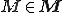 в том и только том случае, когда
в том и только том случае, когда  постоянен Точки
постоянен Точки  и
и  соответственно:
соответственно: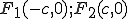
 плоскости такова, что
плоскости такова, что 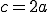 . Здесь
. Здесь  и
и  - фиксированные положительные числа. Таким образом,
- фиксированные положительные числа. Таким образом, 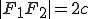 и, как следует из неравенства треугольника,
и, как следует из неравенства треугольника, 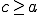 . Однако, если
. Однако, если 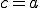 , то либо
, то либо  , либо
, либо  . А это означает, что
. А это означает, что  лежит на одном из лучей, дополняющих до прямой отрезок
лежит на одном из лучей, дополняющих до прямой отрезок 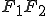 . Поэтому этот случай мы рассматривать не будем.
. Поэтому этот случай мы рассматривать не будем. в координатах:
в координатах: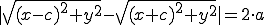 (2)
(2) (2`)
(2`) .
.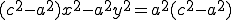 , или, принимая во внимание то, что
, или, принимая во внимание то, что 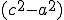 положительно,
положительно, 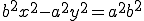 для
для  .
. , получим:
, получим: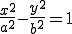 (2*)
(2*) .(*)
.(*)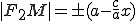 (**).
(**).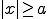 . Кроме того,
. Кроме того, 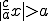 . При положительном
. При положительном 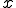 внутри скобок в (*) стоит положительное число, а внутри скобок из (**) - отрицательное число. Поэтому при
внутри скобок в (*) стоит положительное число, а внутри скобок из (**) - отрицательное число. Поэтому при 
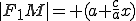 и
и 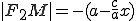 , а
, а  . Случай
. Случай  рассматривается аналогично, и приводит к равенству
рассматривается аналогично, и приводит к равенству  .
.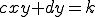 (Ш)
(Ш)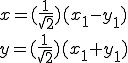
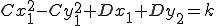 для подходящих
для подходящих 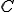 и
и  .(Ш*)
.(Ш*)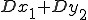 . Для этого сделаем такую замену переменных:
. Для этого сделаем такую замену переменных:
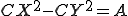 при подходящем значении
при подходящем значении  . Интересующийся читатель сможет без труда установить,что
. Интересующийся читатель сможет без труда установить,что  . Как хорошо известно, эту параболу можно сдвинуть по плоскости так, что ее вершина окажется в начале координат, а уравнение примет вид
. Как хорошо известно, эту параболу можно сдвинуть по плоскости так, что ее вершина окажется в начале координат, а уравнение примет вид  . Мы, как и выше поступили с гиперболой, дадим геометрическое определение параболы и получим ее каноническое уравнение.
. Мы, как и выше поступили с гиперболой, дадим геометрическое определение параболы и получим ее каноническое уравнение.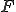 на плоскости и прямую
на плоскости и прямую 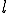 , которая не проходит через
, которая не проходит через  , а
, а 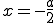 .
.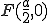 и
и 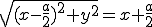 .
. , откуда получается
, откуда получается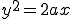 (3)
(3) , из чего следует, что
, из чего следует, что 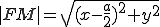 . Заменяя здесь
. Заменяя здесь 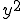 на
на  из (3), получим
из (3), получим 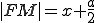 . То есть
. То есть 


