
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эллипс. Вывод канонического уравнения. Свойства.Содержание книги
Поиск на нашем сайте
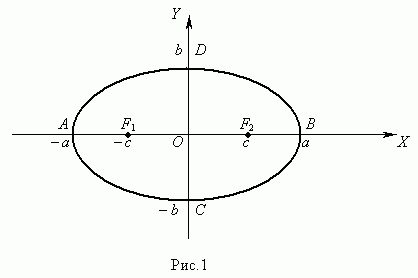
Опр: Эллипсом наз сножесто точек плоскости, сумма расстояний от которых до 2 заданных точек есть величина постоянная.Заданые точки – наз фокусами эллипса.(F1,F2)
5) Параметрические ур-ния эллипса: 6) Эксцентриситет
Гипербола. Вывод канонического уравнения. Свойства. Асимптоты Гиперболой наз множеатво точек плоскости модуль разницы расстояний от которых до двух заданных точек есть величина постоянная. Две заданные точки наз фокусами.
5)Из окружности 6) 7) Эксцентриситет
Парабола. Вывод канонического уравнения. Свойства. Параболой наз множество точек плоскости расстояние от которых до зад точки (фокуса) и до заданной прямой (директрисы) равно.
|MK|=|MF| р- фокальный параметр.
Родство эллипса, гиперболы и параболы. Кривая второго порядка - это множество точек плоскости для которых отношение расстояния до заданной точки (фокуса) и до заданной прямой (директрисы) есть величина постоянная равная а) б) в) Опр: Кривая второго порядка наз центральной, если она имеет один центр симметрии и не центральной или гиперболич, если имеет бесконечное множество центров симметрии, или не имеет. Общее ур-ние кривой: 5.Преобразование прям д с к. 1)Параллельный перенос: Рассмотрим точку М. У нее были корд (х,у) в старой системе корд. и 2) Поворот прям д с к вокруг начала корд на угол альфа. М(х,у) в старой системе корд.
3) Общее преобразование прямоуг д с к, состоит из поворота и переноса. 1] а)параллельный перенос начала координат на Матрица перехода:
6. Общ ур линий второго порядка Центральные линии).
1этап) Если ур-ие не содержит xy то первый этам можно пропустить. Если b не равн нулю:
Пусть Второй этап: ((центр кривые)) 1) если 2) если 3) если 4) если 5) если Теорема: ((в след билете)) НЕцентральные линии).
1этап) Если ур-ие не содержит xy то первый этап можно пропустить. Если b не равн нулю:
Пусть
Второй этап: ((нецентр кривые)) 1) если если 2) если 3) если 4) если Теорема: Пусть в прямоуг д.с.к. задано ур крив втор порядка. Существует такая прямоуг д.с.к. в которой ур-ие принимает один из девяти кон видов.((перечислены выше))
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 379; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.249.191 (0.008 с.) |

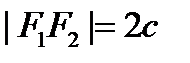 ;
; 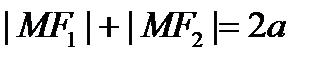 , т.е. а и с- параметры, а>c
, т.е. а и с- параметры, а>c  ;
;  ;
; 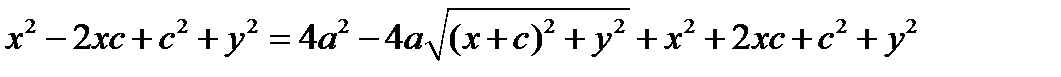 ;
; 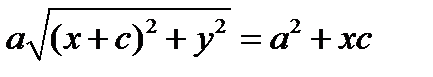 ;
; 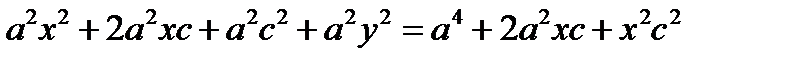 ;
; 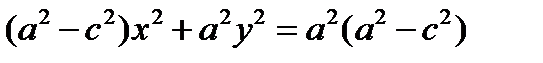 т.к. a>c, то
т.к. a>c, то 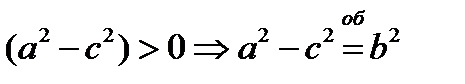 ;
; 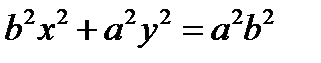 ;
; 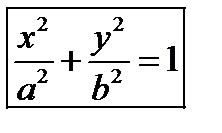 - канонич ур-ние эллипса в канонич системе координат. a и b- параметры, а- большая полуось b- малая полуось. Свойства: 1) пересечение с осями координат: с Ох:
- канонич ур-ние эллипса в канонич системе координат. a и b- параметры, а- большая полуось b- малая полуось. Свойства: 1) пересечение с осями координат: с Ох: 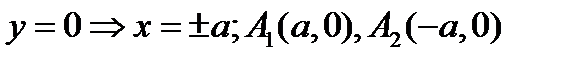 с Оу
с Оу 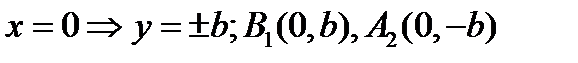 ;
; 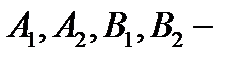 вершины эллипса. 2) Симметричность:
вершины эллипса. 2) Симметричность: 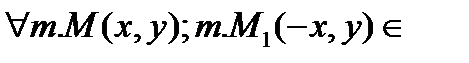 эллипсу => эллипс симметричен относительно Оу.
эллипсу => эллипс симметричен относительно Оу. 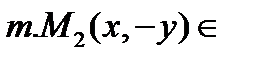 эллипсу => симметричен относит Ох
эллипсу => симметричен относит Ох 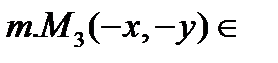 эллипсу => О-ценр симметрии эллипса. 3) Эллипс расположен в ограниченной части плоскости
эллипсу => О-ценр симметрии эллипса. 3) Эллипс расположен в ограниченной части плоскости 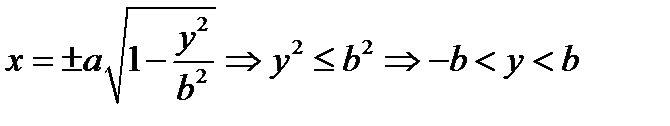 ;
; 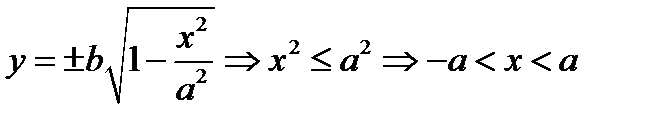 4) Эллипс можно получить из окружности с помощью сжатия или растяжения
4) Эллипс можно получить из окружности с помощью сжатия или растяжения 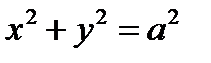 ;
; 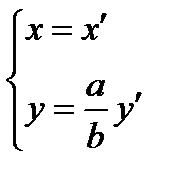 ;
; 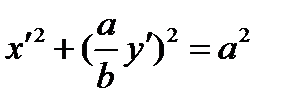 ;
; 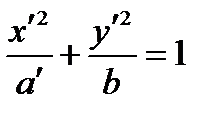
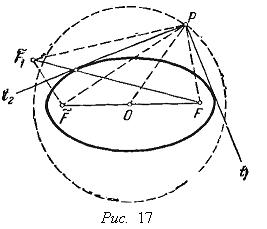
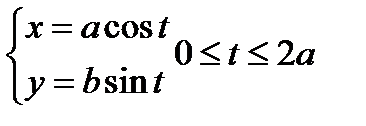
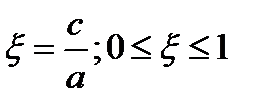 ;
; 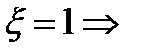 отрезок;
отрезок; 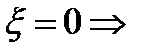 окружность(с=0).
окружность(с=0). 
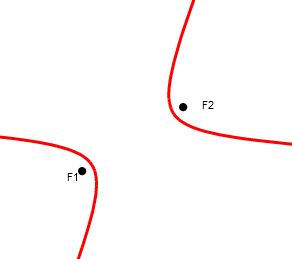
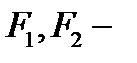 фокусы.
фокусы. 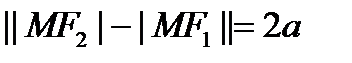 , a<c. Если
, a<c. Если 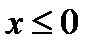 - модуль опускается со знаком минус. Если
- модуль опускается со знаком минус. Если 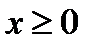 , со знаком плюс.
, со знаком плюс. 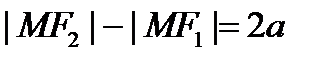 ;
; 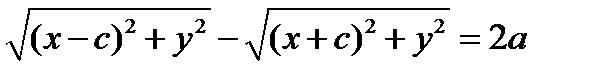 ;
; 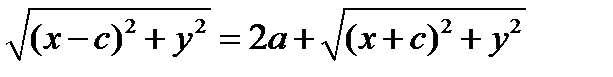 ;
; 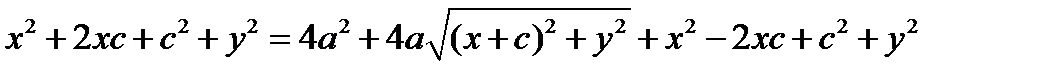 ;
; 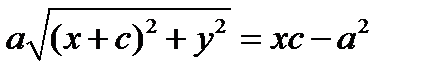 ;
; 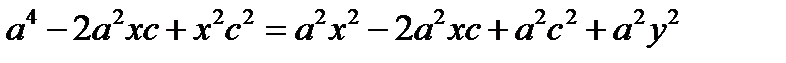 ;
; 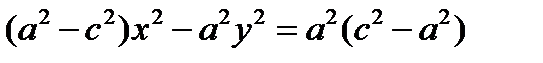 т.к. a<c, то
т.к. a<c, то 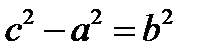 ;
; 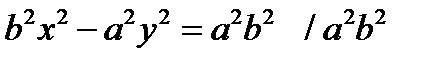 ;
; 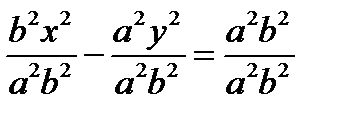
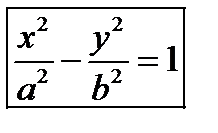 - каноническое ур-ние в канонической системе координат. а(Ох)- действит полуось, b(Оу)- мнимая. Свойства: 1) пересечение с осями: с Ох:
- каноническое ур-ние в канонической системе координат. а(Ох)- действит полуось, b(Оу)- мнимая. Свойства: 1) пересечение с осями: с Ох: 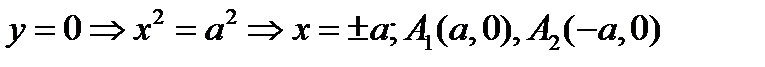 - вершина. с Оу
- вершина. с Оу 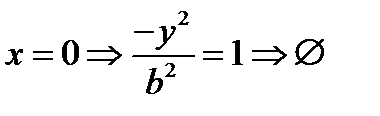 не пересек. 2) Симметрия: а)
не пересек. 2) Симметрия: а) 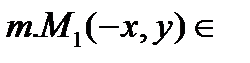 гиперб=> симметричен отност Оу. б)
гиперб=> симметричен отност Оу. б) 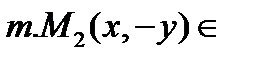 гиперб => симмет относит Ох в)
гиперб => симмет относит Ох в) 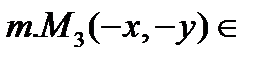 гипеб => центрально симметр относит начала координат 3)
гипеб => центрально симметр относит начала координат 3) 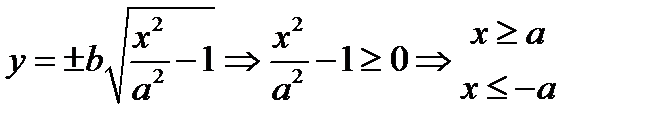 не является ограниченной. 4) Асимптоты- прямые к которым кривые неограниченно приближ удаляясь в бесконечность.
не является ограниченной. 4) Асимптоты- прямые к которым кривые неограниченно приближ удаляясь в бесконечность. 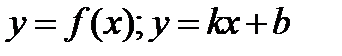 наклонная асимптота. Если асимптота
наклонная асимптота. Если асимптота 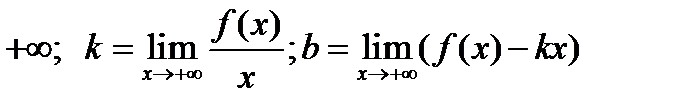 если в
если в 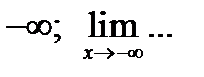 ;
; 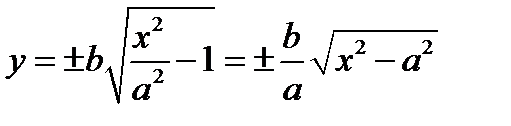 Рассмотрим случай:
Рассмотрим случай:  ;
; 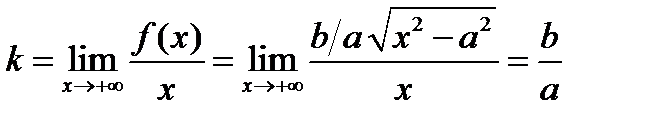 ;
; 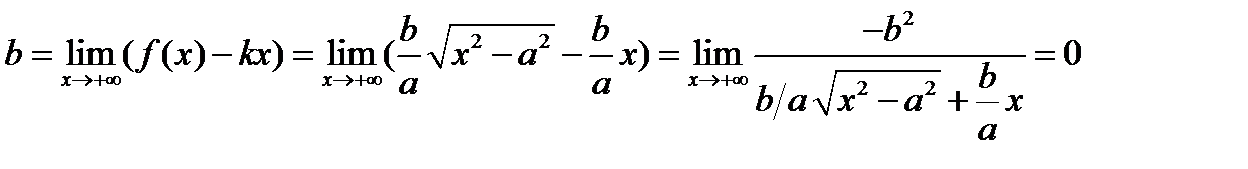 . Асимптоты в +бесконечн
. Асимптоты в +бесконечн 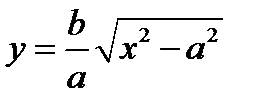 ,
, 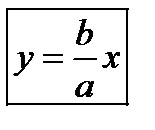 Асимптоты в -бесконечн
Асимптоты в -бесконечн 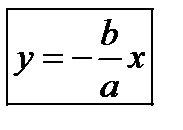
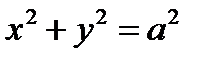 ;
; 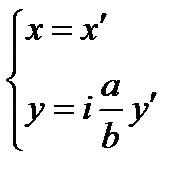
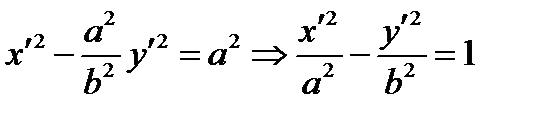
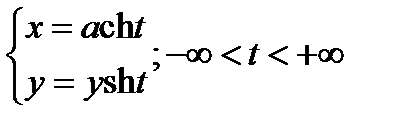 ;
; 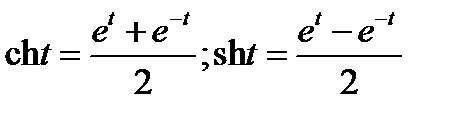
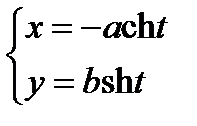
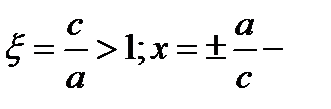 директрисы
директрисы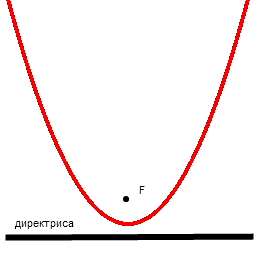
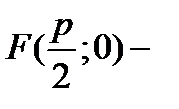 фокус.
фокус. 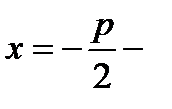 директриса. |MK|=|MF|
директриса. |MK|=|MF| 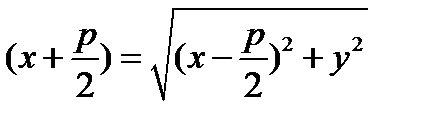 ;
; 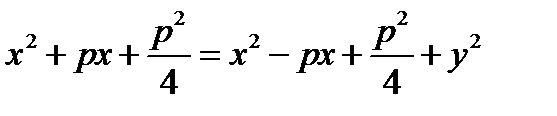 ;
; 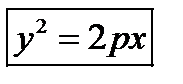 - канонич ур-ние. Свойства: 1) пересечение с осями:
- канонич ур-ние. Свойства: 1) пересечение с осями: 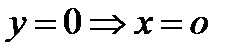 О(0,0)-вершина. 2) Симметричность:
О(0,0)-вершина. 2) Симметричность: 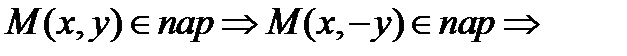 симметричн относ Ох. 3)параметри ур-ние:
симметричн относ Ох. 3)параметри ур-ние: 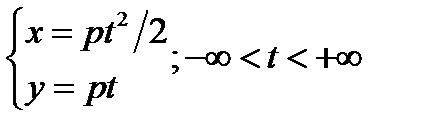 4)
4) 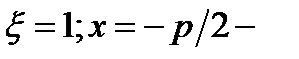 директриса.
директриса.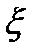 .
.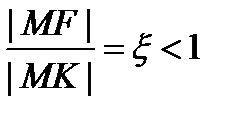
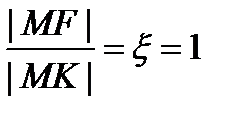
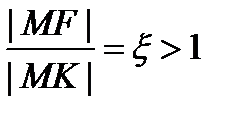
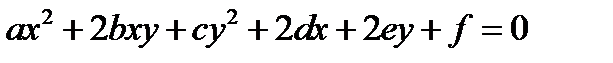
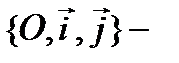 старая система кооорд.
старая система кооорд. 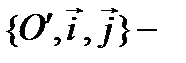 новая.
новая.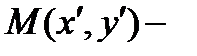 в новой.
в новой. 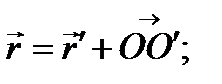
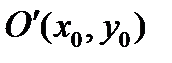 - в старой.
- в старой. 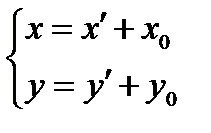 ;
; 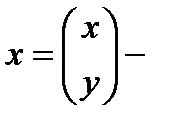 координатный столбец точки М в старой с к.
координатный столбец точки М в старой с к. 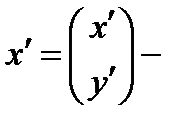 корд точки М в новой.
корд точки М в новой. 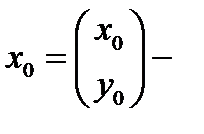 корд точки
корд точки 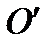 в старой с.к. <~ Связь между
в старой с.к. <~ Связь между 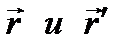 .
.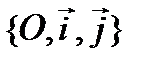 и
и 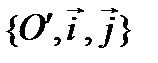
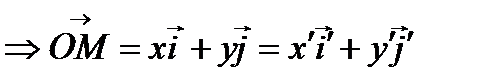 .
. 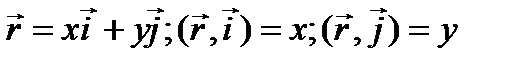 ;
; 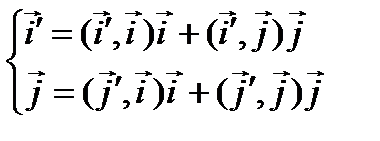 ;
; 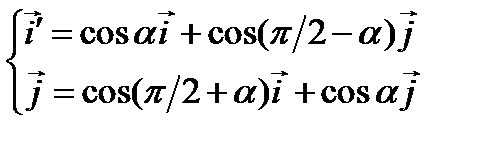 ;
; 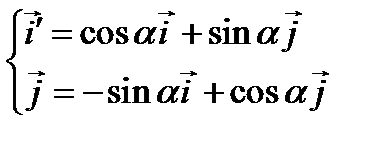 ;
; 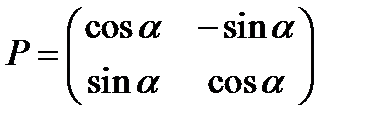 detP=1. P- матрица перехода от старого базиса
detP=1. P- матрица перехода от старого базиса 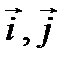 к новому
к новому 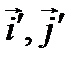
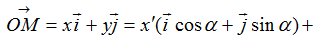
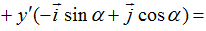
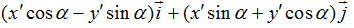
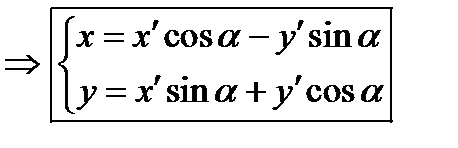
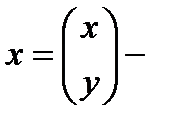 координатный столбец в старой с.к.
координатный столбец в старой с.к. 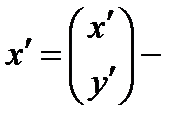 в новой.
в новой. 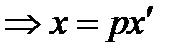
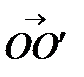 б) поворот относительно
б) поворот относительно 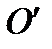
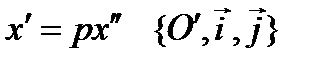 ;
; 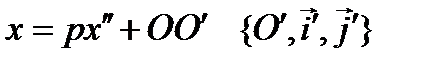
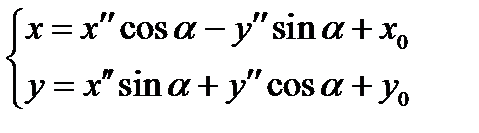 2] а)поворот с.к. относительно О б) Перенос относительно носой с.к.
2] а)поворот с.к. относительно О б) Перенос относительно носой с.к. 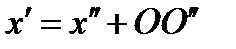 композиция
композиция 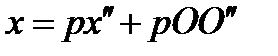 ;
; 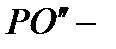 корд столбец нового начала координат.
корд столбец нового начала координат. ((далее тупо подставить в ур крив)) …
((далее тупо подставить в ур крив)) …

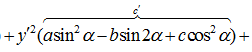
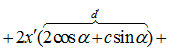

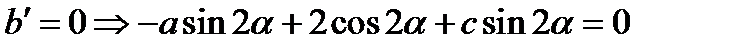 ; 1 случай) если а=с
; 1 случай) если а=с  ; 2 случ) если
; 2 случ) если  ; После первого этапа ур кривой бедет иметь вид:
; После первого этапа ур кривой бедет иметь вид: 
 ;
;  ;
; 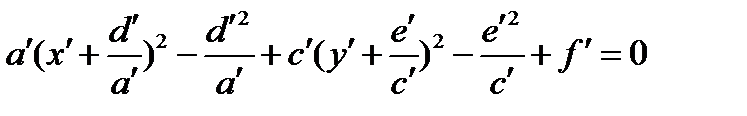 ;
;  ;
; 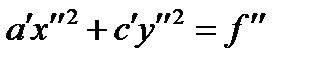 , где
, где  Если
Если  ;
; - эллипс
- эллипс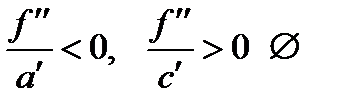 - мнимый эллипс
- мнимый эллипс разных знаков - гипербола
разных знаков - гипербола одного знака – пара мнимых пересек прямых (
одного знака – пара мнимых пересек прямых ( )
) )
)

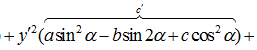
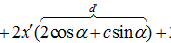

 либо
либо  ; пусть
; пусть 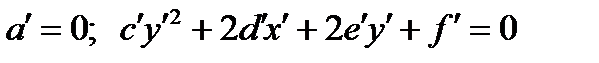 ;
;  ;
; 
 :
:  ;
;  ;
;  - порабола
- порабола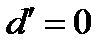 :
:  ;
;  (пар перенос)
(пар перенос)  , где
, где 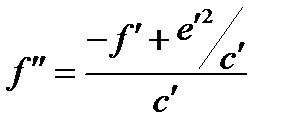
 - пара парал прямых
- пара парал прямых - пара мнимых парал прямых
- пара мнимых парал прямых - пара совп прямых
- пара совп прямых


