
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация кривых 2-го порядка.Содержание книги
Поиск на нашем сайте
Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
в котором по крайней мере один из коэффициентов
Классификация кривых второго порядка: Невырожденные кривые Кривая второго порядка называется невырожденной, если § Невырожденная кривая второго порядка называется центральной, если § эллипс — при условии D > 0 и Δ I < 0; § частный случай эллипса — окружность — при условии § I 2 = 4 D или a 11 = a 22, a 12 = 0; § мнимый эллипс (ни одной вещественной точки) — при условии Δ I > 0; § гипербола — при условии D < 0; § Невырожденная кривая второго порядка называется нецентральной, если Δ I = 0 § парабола — при условии D = 0. Вырожденные кривые Кривая второго порядка называется вырожденной, если Δ = 0. Могут возникать следующие варианты: § вещественная точка на пересечении двух мнимых прямых (вырожденный эллипс) — при условии D > 0; § пара вещественных пересекающихся прямых (вырожденная гипербола) — при условии D < 0; § вырожденная парабола — при условии D = 0: § пара вещественных параллельных прямых — при условии B < 0; § одна вещественная прямая (две слившиеся параллельные прямые) — при условии B = 0; § пара мнимых параллельных прямых (ни одной вещественной точки) — при условии B > 0. Эллипсоид. Канон ур-ие. Сечения. Эллипсоиды вращения.
-Сечение плоскостью xOy
-эллипсоид вращения
1) xOy: z=0; 2) xOz: y=0;
3) yOz: x=0; 4) б) |h|>|c| - пустое множество в) |h|=|c| две точки (0,0,c) и (0,0,-c) Вращение: вращать эллипс
Гипербалоиды Однополостный:
1) yOz: 2) xOz: 3) Прямолинейной образующей поверхности назовем прямую целиком лежащую на поверхности. Теорема: через каждую точку однополостного гипербалоида проходят две прямолинейных образующих. Д-во: Вращение гиперболы Двухполостный:
-двуполосный гиперболоид 1) yOz: 2) xOz:
3) б) |h|<|c| - пустое множество в) |h|=|c| - 2 точки (0,0,c) и (0,0,-c) Вращение гиперболы
-двуполосный вращение
Конус.
1) 2) 3) б) h=0 – 1 точка (0,0,0) – вершина ЗЫ Конус – асимптотическая поверхность для гипербалоидОВ
Параболоиды Эиптический
а - эллиптический;
1) 1) 3) б) h=0 – 1 тчк (0,0,0) в) h>0 эллипс с полуосями
Гипербалический
б - гиперболический
-Изображение гиперболического параболоида с помощью сечений
1) 1) 3) б) h=0: в) h>0 гипербола с действ осью х и мнимой у Теорема: Через каждуйю точку гиперболич параб проходят 2 прямые лежащ на нем. Д-во:
Цилиндры Цилиндром наз поверхность, которая получ при движении прямой в простр не меняющей своего напрв. Если данная прямая параллельна Oz, то цилиндр опред ур-ием сечения xOy, т.е. z=0 Эллиптический
Гипербалический
Изображение гипербоического цилиндра с помощью сечений
Пораболический
Изображение параболического цилиндра с помощью сечений Прямолинейныеобразующие: поверхности, бесконечная система прямых линий (или отрезков прямых линий), целиком заполняющих поверхность. Поверхность, состоящая из прямых линий, называется линейчатой. Поверхности, имеющие два семейства прямолинейных образующих, суть поверхности второго порядка.
|
||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.186.109 (0.005 с.) |



 отличен от нуля.
отличен от нуля.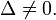 Могут возникать следующие варианты:
Могут возникать следующие варианты:

 - Сечения эллипсоида координатными плоскостями
- Сечения эллипсоида координатными плоскостями
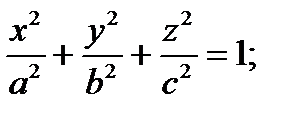 a,b,c>0 – полуоси;
a,b,c>0 – полуоси;

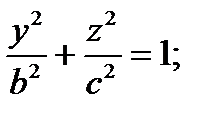
 ; а)
; а)  эллипс с полуосями
эллипс с полуосями  (чем |h| больше, тем полуоси меньше);
(чем |h| больше, тем полуоси меньше); или Oy:
или Oy: 

 - сечение однополосного гиперболойда 2-мя плоскостями
- сечение однополосного гиперболойда 2-мя плоскостями - сечение однополосного гиперболойда
- сечение однополосного гиперболойда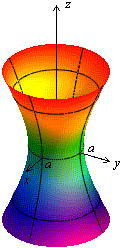 -однополосный вращение
-однополосный вращение
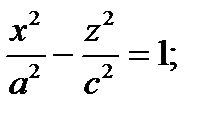
 ; а)
; а) 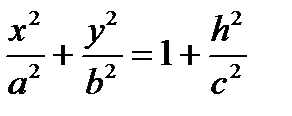 эллипс с полуосями
эллипс с полуосями  (чем |h| больше, тем полуоси больше);
(чем |h| больше, тем полуоси больше); 
 ;
;  ;
;  - ур-ия двух пл-стей (первая прямая);
- ур-ия двух пл-стей (первая прямая);  - вторая прямая
- вторая прямая вокруг Oz:
вокруг Oz: 
 - Сечения двуполостного гиперболоида плоскостью xOz
- Сечения двуполостного гиперболоида плоскостью xOz
 - гипербола с действ осью z и мнимой у
- гипербола с действ осью z и мнимой у - гипербола с действ осью z и мнимой х
- гипербола с действ осью z и мнимой х а) эллипс с полуосями
а) эллипс с полуосями 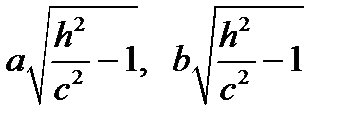 (чем |h| больше, тем полуоси больше);
(чем |h| больше, тем полуоси больше); вокруг Oz:
вокруг Oz: 
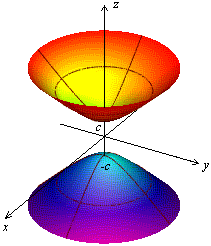


 - две прямые
- две прямые - две прямые
- две прямые а) эллипс с полуосями
а) эллипс с полуосями  (чем |h| больше, тем полуоси больше);
(чем |h| больше, тем полуоси больше);

 - Сечения эллиптического параболоида координатными плоскостями
- Сечения эллиптического параболоида координатными плоскостями - парабола
- парабола - парабола
- парабола а) h<0 – беск множ-во
а) h<0 – беск множ-во
 -Дополнительные сечения параболоида
-Дополнительные сечения параболоида -параболойд вращения
-параболойд вращения

 - парабола ветви вниз
- парабола ветви вниз а) h<0 – гипербола с действ осью у и мнимой х
а) h<0 – гипербола с действ осью у и мнимой х - две прямые
- две прямые
 ;
;  - перв прям и
- перв прям и 

 Изображение эллиптического цилиндра с помощью сечений
Изображение эллиптического цилиндра с помощью сечений






