
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Базис множества всех векторов в трехмерном пространстве.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Вектор.Свойства. Вектор - направленный отрезок, нулевой вектор-точка. Длина вектора- длина отрезка вектора или расстояние от начала до конца. Два вектора равные если: лежат на парал. прямых или на одной. их длины равны, напр в одну сторону. Векторы, которые лежат на парал прямых или на одной- коллинеарные, 2 коллин. вектора напр в одну сторону- соноправл., в разнае стороны- противополнапр. векторы лежащ на парал прямых – компланарные. Операции: 1.Сложение: правило треуг, правило парал-рама. 2.Умножение вектора на число: Произведение вектора А на число Свойства операций: 1)А+В=В+А, 2)(А+В)+С=А+(В+С), 3)А+0=А, 4) Для А = |aA|+|bA|=|aA+bA|| Направл: Множество векторов, замкнутое относительно линейных операций, называется векторным пространством. Если одно векторное пространство является подмножеством другого, то оно называется его подпространством.
Проекция на ось. Опр: Осью наз прямую на которой задано направл. Оно задается произвольным не 0вым вектором. Опр: Рассм множество векторов плоскости.
-проекция вектора на ось(рис) Рассм произв ось. Пусть l прямая пересек ось в произв точке. Еще есть точка М(не лежащая на оси). Проводим через нее прямую || l. Получаем 1)
1) 2)
3 ) Линейная зависимость и независимость системы векторов. Базис векторного пространства. Разложение вектора по базису. Координаты вектора. Арифметические свойства координат вектора. Система векторов a1,...,ak называется линейно независимой, если нулевой вектор раскладывается по ней единственным образом. Система векторов a1,..., аk, линейно зависима, если нулевой вектор раскладывается по ней не единственным образом, т. е. если найдутся такие коэффициенты α1,...,αk что α1a1 +... + αkаk = 0, но не все они равны нулю: а1^2+... + аk^2≠ 0. Базисом в векторном пространстве называется упорядоченная линейно независимая система векторов такая, что любой вектор этого пространства по ней раскладывается. Чтобы разложить, вектор b по базисным векторам a1,..., an, необходимо найти коэффициенты x1,...,xn, при которых линейная комбинация векторов a1,...,an равна вектору b. Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору. Равные векторы в единой системе координат имеют равные координаты Координаты коллинеарных векторов пропорциональны:
Квадрат длины вектора равен сумме квадратов его координат: При умножении вектора на действительное число каждая его координата умножается на это число:
При сложении векторов соответствующие координаты векторов складываются:
Скалярное произведение двух векторов равно сумме произведений их соответствующих координат:
Векторное произведение двух векторов можно вычислить с помощью определителя матрицы
Аналогично, смешанное произведение трех векторов можно найти через определитель
4.Базис множества всех векторов на прямой и плоскости. Теорема1: Произвольный не 0ой вектор обр базис множества всех векторов прямой. Док-во: Рассмотрим любой
2 произвнеколинеарн вектора обр базис множества всех векторов плоскости. Док-во: Пусть 2)
Уравн линий и поверхн Параметрические уравнения линий и поверхностей. Алгебраические линии и поверхности. Примеры.
Линия на плоск – это множество точек, координаты которых удовл F(x,y)=0, данное ур-е должно иметь решение и не должно быть тождеством, в этом случае говорят, что кривая задана не явно. Если кривая задается множ-ом тчк y=f(x)– явно. (x+1024y-1100=0 - прямая). Если в неявном ур-ии кривой F(x,y)=0, F(x,y) – многочлен относ x,y то такая кривая – алгебраическая. Степень данного мн-на порядок кривой. Если F(x,y) нельзя представить в виде мн-на относ x,y то кривая назыв трансцендентной. (Ax+By+C=0 – алг, y=cosx - трансц). Параметрич ур-ями кривой наз ур-ия вида , где t – параметр, котор приним знач от а до b (a≤t≤b) F(x,y)=0 => F(x(t),y(t))=0 (y-kx-b=0 Поверхностью в 3д пространсте назыв множ-во тчк корд-ты кот-ых удовл: F(x,y,z)=0 если пов-сть задается z=z(x,y) то говорят что пов-сть задана явно (Ур-ие F(x,y,z)=0 имеет реш и не явл тожд) (x,y,z) – прям.д.с.к. (Ax+By+Cz+D=0) (про мн-ны, алг и трансц тоже самое) парам-ское Ур-ие:,
u,v – парам. Кривая может быть задана как пересечение двух поверхностей или парам ур. (x=x(t) и тд) 5.Прямые и плоскости 6. Центральные линии).
1этап) Если ур-ие не содержит xy то первый этам можно пропустить. Если b не равн нулю:
Пусть Второй этап: ((центр кривые)) 1) если 2) если 3) если 4) если 5) если Теорема: ((в след билете)) НЕцентральные линии).
1этап) Если ур-ие не содержит xy то первый этап можно пропустить. Если b не равн нулю:
Пусть
Второй этап: ((нецентр кривые)) 1) если если 2) если 3) если 4) если Теорема: Пусть в прямоуг д.с.к. задано ур крив втор порядка. Существует такая прямоуг д.с.к. в которой ур-ие принимает один из девяти кон видов.((перечислены выше)) Невырожденные кривые Кривая второго порядка называется невырожденной, если § Невырожденная кривая второго порядка называется центральной, если § эллипс — при условии D > 0 и Δ I < 0; § частный случай эллипса — окружность — при условии § I 2 = 4 D или a 11 = a 22, a 12 = 0; § мнимый эллипс (ни одной вещественной точки) — при условии Δ I > 0;
§ гипербола — при условии D < 0; § Невырожденная кривая второго порядка называется нецентральной, если Δ I = 0 § парабола — при условии D = 0. Вырожденные кривые Кривая второго порядка называется вырожденной, если Δ = 0. Могут возникать следующие варианты: § вещественная точка на пересечении двух мнимых прямых (вырожденный эллипс) — при условии D > 0; § пара вещественных пересекающихся прямых (вырожденная гипербола) — при условии D < 0; § вырожденная парабола — при условии D = 0: § пара вещественных параллельных прямых — при условии B < 0; § одна вещественная прямая (две слившиеся параллельные прямые) — при условии B = 0; § пара мнимых параллельных прямых (ни одной вещественной точки) — при условии B > 0. Гипербалоиды Однополостный:
1) yOz: 2) xOz: 3) Прямолинейной образующей поверхности назовем прямую целиком лежащую на поверхности. Теорема: через каждую точку однополостного гипербалоида проходят две прямолинейных образующих. Д-во: Вращение гиперболы Двухполостный:
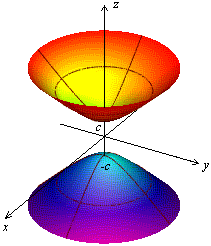
-двуполосный гиперболоид 1) yOz: 2) xOz:
3) б) |h|<|c| - пустое множество в) |h|=|c| - 2 точки (0,0,c) и (0,0,-c) Вращение гиперболы
-двуполосный вращение
Конус.
1) 2) 3) б) h=0 – 1 точка (0,0,0) – вершина ЗЫ Конус – асимптотическая поверхность для гипербалоидОВ
Параболоиды Эиптический
а - эллиптический;
1) 1) 3) б) h=0 – 1 тчк (0,0,0) в) h>0 эллипс с полуосями
Гипербалический
б - гиперболический
-Изображение гиперболического параболоида с помощью сечений
1) 1) 3) б) h=0: в) h>0 гипербола с действ осью х и мнимой у Теорема: Через каждуйю точку гиперболич параб проходят 2 прямые лежащ на нем. Д-во:
Цилиндры Цилиндром наз поверхность, которая получ при движении прямой в простр не меняющей своего напрв. Если данная прямая параллельна Oz, то цилиндр опред ур-ием сечения xOy, т.е. z=0 Эллиптический
Гипербалический
Изображение гипербоического цилиндра с помощью сечений
Пораболический
Изображение параболического цилиндра с помощью сечений Прямолинейныеобразующие: поверхности, бесконечная система прямых линий (или отрезков прямых линий), целиком заполняющих поверхность. Поверхность, состоящая из прямых линий, называется линейчатой. Поверхности, имеющие два семейства прямолинейных образующих, суть поверхности второго порядка.
Поверхности вращения.
Вектор.Свойства. Вектор - направленный отрезок, нулевой вектор-точка. Длина вектора- длина отрезка вектора или расстояние от начала до конца. Два вектора равные если: лежат на парал. прямых или на одной. их длины равны, напр в одну сторону. Векторы, которые лежат на парал прямых или на одной- коллинеарные, 2 коллин. вектора напр в одну сторону- соноправл., в разнае стороны- противополнапр. векторы лежащ на парал прямых – компланарные. Операции: 1.Сложение: правило треуг, правило парал-рама. 2.Умножение вектора на число: Произведение вектора А на число Свойства операций: 1)А+В=В+А, 2)(А+В)+С=А+(В+С), 3)А+0=А, 4) Для А = |aA|+|bA|=|aA+bA|| Направл: Множество векторов, замкнутое относительно линейных операций, называется векторным пространством. Если одно векторное пространство является подмножеством другого, то оно называется его подпространством.
Проекция на ось. Опр: Осью наз прямую на которой задано направл. Оно задается произвольным не 0вым вектором. Опр: Рассм множество векторов плоскости.
-проекция вектора на ось(рис) Рассм произв ось. Пусть l прямая пересек ось в произв точке. Еще есть точка М(не лежащая на оси). Проводим через нее прямую || l. Получаем 1)
1) 2)
3 ) Линейная зависимость и независимость системы векторов. Базис векторного пространства. Разложение вектора по базису. Координаты вектора. Арифметические свойства координат вектора. Система векторов a1,...,ak называется линейно независимой, если нулевой вектор раскладывается по ней единственным образом. Система векторов a1,..., аk, линейно зависима, если нулевой вектор раскладывается по ней не единственным образом, т. е. если найдутся такие коэффициенты α1,...,αk что α1a1 +... + αkаk = 0, но не все они равны нулю: а1^2+... + аk^2≠ 0. Базисом в векторном пространстве называется упорядоченная линейно независимая система векторов такая, что любой вектор этого пространства по ней раскладывается. Чтобы разложить, вектор b по базисным векторам a1,..., an, необходимо найти коэффициенты x1,...,xn, при которых линейная комбинация векторов a1,...,an равна вектору b. Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору. Равные векторы в единой системе координат имеют равные координаты Координаты коллинеарных векторов пропорциональны:
Квадрат длины вектора равен сумме квадратов его координат: При умножении вектора на действительное число каждая его координата умножается на это число:
При сложении векторов соответствующие координаты векторов складываются:
Скалярное произведение двух векторов равно сумме произведений их соответствующих координат:
Векторное произведение двух векторов можно вычислить с помощью определителя матрицы
Аналогично, смешанное произведение трех векторов можно найти через определитель
4.Базис множества всех векторов на прямой и плоскости. Теорема1: Произвольный не 0ой вектор обр базис множества всех векторов прямой. Док-во: Рассмотрим любой 2 произвнеколинеарн вектора обр базис множества всех векторов плоскости. Док-во: Пусть 2)
Базис множества всех векторов в трехмерном пространстве. Теорема3: 3 произв некомпл вектора обр базис множества векторов 3-х мерного пространства. Док-во: Пусть
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 533; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.131.11 (0.014 с.) |

 наз В: 1) В колинеарен А, 2) соноправлен, есль
наз В: 1) В колинеарен А, 2) соноправлен, есль  0, В коллин А, тогда
0, В коллин А, тогда 
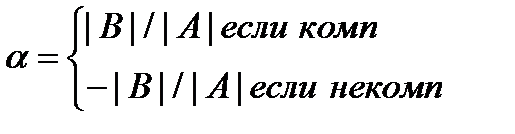 Единственность: Пусть сущ
Единственность: Пусть сущ  и
и  => В=|
=> В=|  |*|А| => |
|*|А| => |  2;
2; 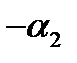 (не может).
(не может). В: А+В=0. Опр: Разностью А-В=А+(-В). 5)
В: А+В=0. Опр: Разностью А-В=А+(-В). 5)  )А=
)А=  =>
=> 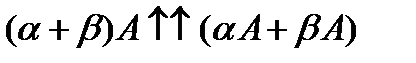 ;
;  =>
=>  ,
, 
 }=>
}=> 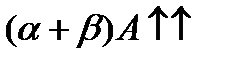
 . 2)
. 2)  ,
,  ,
,  ,
,  }=>
}=>  .Длина:
.Длина:  . 7)
. 7) 
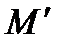 -проекцию точки на ось вектора А || l
-проекцию точки на ось вектора А || l  . Опр: Рассм множество всех векторов 3-х метром пространстве. Берется ось, через нее проводится плоскость Пи. Берется М, через нее проводится еще одна плоскость || Пи
. Опр: Рассм множество всех векторов 3-х метром пространстве. Берется ось, через нее проводится плоскость Пи. Берется М, через нее проводится еще одна плоскость || Пи  . Алгебраич значением проекции вектора на ось наз число которое опр след образом:
. Алгебраич значением проекции вектора на ось наз число которое опр след образом: 
 Свойства алгебр значений:
Свойства алгебр значений: 2)
2)  . Опр: Под углом между векторами будем принимать угол между векторами равных данным и имеющими общее начало и абсолютной величине не больше 180. По часовой угол с минусом, против +. Опр: Рассм проекциб вектора на ось || l или || плоскости Пи., если эта прямая или плоскость перпендик оси, то она ортогональна. Теорема: Алгебр значение ортогональной проекции АВ на ось вектора а
. Опр: Под углом между векторами будем принимать угол между векторами равных данным и имеющими общее начало и абсолютной величине не больше 180. По часовой угол с минусом, против +. Опр: Рассм проекциб вектора на ось || l или || плоскости Пи., если эта прямая или плоскость перпендик оси, то она ортогональна. Теорема: Алгебр значение ортогональной проекции АВ на ось вектора а  Док-во:
Док-во: , проводим ||AB из точки С (лежащей на оси), получается CD
, проводим ||AB из точки С (лежащей на оси), получается CD  => т.к. длины АВ и CD равны =>
=> т.к. длины АВ и CD равны => 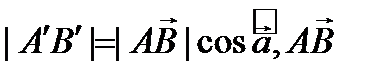
 ,
, 
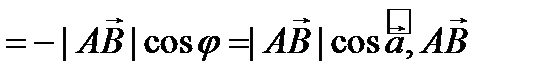 .
. Подразумевается, что координаты вектора
Подразумевается, что координаты вектора  не равны нулю.
не равны нулю.

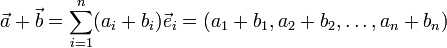

 где
где 


 1)
1)  -лин независ система векторов,т.к.
-лин независ система векторов,т.к.  =>
=>  =>
=>  =>
=> 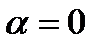 . 2) Любой произвольный вектор принадлеж прямой.
. 2) Любой произвольный вектор принадлеж прямой.  коллинеарен
коллинеарен 
 :
: 
 координата вектора в базисе
координата вектора в базисе  произ неколин векторы. 1)
произ неколин векторы. 1)  лин независ система векторов, т.к. оба они не равно нулю, т.к. о коллинеарен всем. Подставл в лин комбинацию:
лин независ система векторов, т.к. оба они не равно нулю, т.к. о коллинеарен всем. Подставл в лин комбинацию:  , от обратного. Пусть
, от обратного. Пусть 

 противоречие. =>
противоречие. => 
 .
. 
 базис на АВ.
базис на АВ. 
 базис на АС=>
базис на АС=> 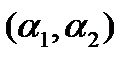 координаты вектора
координаты вектора 


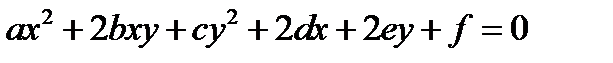 Приведение к конанич виду в два этапа: на первом - поворос с.к. таким образом что бы ур-ие не содержало xy (т.е. b|=0). На втором – параллельный перенос с.к.
Приведение к конанич виду в два этапа: на первом - поворос с.к. таким образом что бы ур-ие не содержало xy (т.е. b|=0). На втором – параллельный перенос с.к. ((далее тупо подставить в ур крив)) …
((далее тупо подставить в ур крив)) …

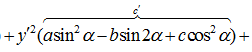
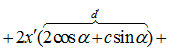

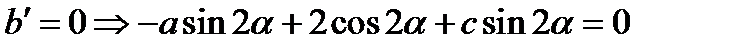 ; 1 случай) если а=с
; 1 случай) если а=с  ; 2 случ) если
; 2 случ) если  ; После первого этапа ур кривой бедет иметь вид:
; После первого этапа ур кривой бедет иметь вид: 
 ;
;  ;
; 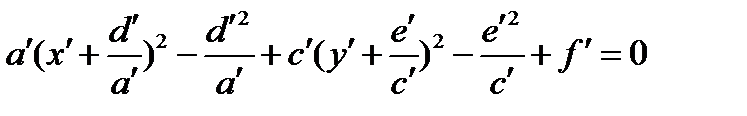 ;
;  ;
; 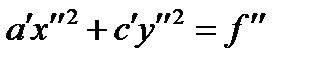 , где
, где  Если
Если  ;
; - эллипс
- эллипс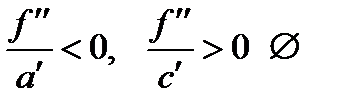 - мнимый эллипс
- мнимый эллипс разных знаков - гипербола
разных знаков - гипербола одного знака – пара мнимых пересек прямых (
одного знака – пара мнимых пересек прямых ( )
) )
)

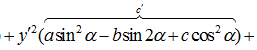
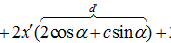

 либо
либо  ; пусть
; пусть 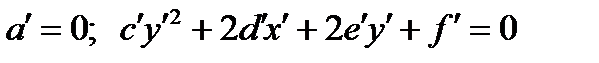 ;
;  ;
; 
 :
:  ;
;  ;
;  - порабола
- порабола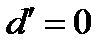 :
:  ;
;  (пар перенос)
(пар перенос)  , где
, где 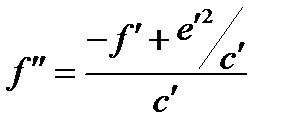
 - пара парал прямых
- пара парал прямых - пара мнимых парал прямых
- пара мнимых парал прямых - пара совп прямых
- пара совп прямых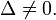 Могут возникать следующие варианты:
Могут возникать следующие варианты:

 - сечение однополосного гиперболойда 2-мя плоскостями
- сечение однополосного гиперболойда 2-мя плоскостями - сечение однополосного гиперболойда
- сечение однополосного гиперболойда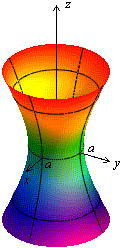 -однополосный вращение
-однополосный вращение
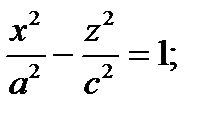
 ; а)
; а) 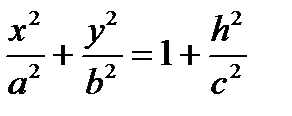 эллипс с полуосями
эллипс с полуосями  (чем |h| больше, тем полуоси больше);
(чем |h| больше, тем полуоси больше); 
 ;
;  ;
;  - ур-ия двух пл-стей (первая прямая);
- ур-ия двух пл-стей (первая прямая);  - вторая прямая
- вторая прямая вокруг Oz:
вокруг Oz: 
 - Сечения двуполостного гиперболоида плоскостью xOz
- Сечения двуполостного гиперболоида плоскостью xOz
 - гипербола с действ осью z и мнимой у
- гипербола с действ осью z и мнимой у - гипербола с действ осью z и мнимой х
- гипербола с действ осью z и мнимой х а) эллипс с полуосями
а) эллипс с полуосями 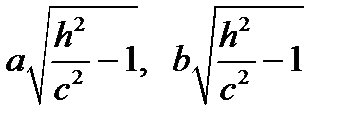 (чем |h| больше, тем полуоси больше);
(чем |h| больше, тем полуоси больше); вокруг Oz:
вокруг Oz: 


 - две прямые
- две прямые - две прямые
- две прямые а) эллипс с полуосями
а) эллипс с полуосями  (чем |h| больше, тем полуоси больше);
(чем |h| больше, тем полуоси больше);

 - Сечения эллиптического параболоида координатными плоскостями
- Сечения эллиптического параболоида координатными плоскостями - парабола
- парабола - парабола
- парабола а) h<0 – беск множ-во
а) h<0 – беск множ-во
 -Дополнительные сечения параболоида
-Дополнительные сечения параболоида -параболойд вращения
-параболойд вращения
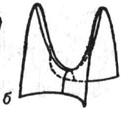

 - парабола ветви вниз
- парабола ветви вниз а) h<0 – гипербола с действ осью у и мнимой х
а) h<0 – гипербола с действ осью у и мнимой х - две прямые
- две прямые
 ;
;  - перв прям и
- перв прям и 

 Изображение эллиптического цилиндра с помощью сечений
Изображение эллиптического цилиндра с помощью сечений



 (вокруг Oz)
(вокруг Oz)  ; Рассмтрим M1 и M2 которые лежат в yOz:
; Рассмтрим M1 и M2 которые лежат в yOz:  кривой,
кривой,  - ур-ие поверхности вращения
- ур-ие поверхности вращения произвольные неколинеарн вектора. 1) Покажем, что
произвольные неколинеарн вектора. 1) Покажем, что  лин независимая система векторов.
лин независимая система векторов.  ,
, 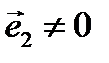 ,
,  .
.  (от обратного)Пусть
(от обратного)Пусть 
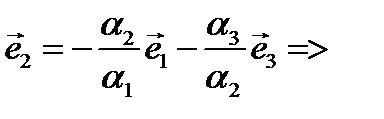
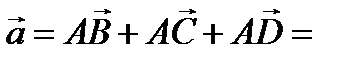
 -базис множества векторов прямой (АВ),
-базис множества векторов прямой (АВ),  - прямой АС
- прямой АС  - прямой АD.
- прямой АD. 

 .
.


