
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Базис пространства, его размерность.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Построение базиса пространства, подпространства несколько упрощается, если мы располагаем некоторыми представлениями о размерности пространства, подпространства. Одним из наводящих соображений здесь может быть следующее. Подмножество Задача 1.1. (№1297[4]) Доказать, что множество Решение. Множество 1.
2.
Кроме того, нетрудно показать, что Линейные подпространства, размерности которых на 1 меньше размерности самого пространства называются гиперплоскостями.
В следующей задаче условий больше. Задача 1.2. (№1298[4]) Доказать, что множество Решение. Для доказательства того, что
Задача 1.3. Проверить, является ли множество Решение. Воспользуемся критерием подпространства. Проверим условие Пусть
так как степень суммы этих двух многочленов равна двум. Итак, множество
Задача 1.4. (№№1291, 1308[4]) Найти какой-нибудь базис и размерность линейного подпространства Решение. Очевидно векторы стандартного базиса
из Попутно решен вопрос (и подтвердилась гипотеза) о размерности
Задача 1.4. (№1306[4]) Пусть Поиск решения. Вспоминаем основные понятия теории квадратичных форм (матрица формы, ранг формы, определение формы). Очевидно, что более подробные записи данного уравнения в виде
В процессе дальнейших размышлений начинаем понимать, что мы должны исходить из неотрицательной определенности формы
а множество решений уравнения
Где Решение. По теореме о приведении квадратичной формы к нормальному виду существует невырожденное линейное преобразование
Множество решений уравнения
Обозначим
Пусть
Очевидно и другое:
Кроме того, система
Отсюда
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 623; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.2 (0.007 с.) |

 векторов пространства
векторов пространства  выделяется из
выделяется из 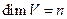 , а
, а  условий специального вида, то есть основания ожидать, что
условий специального вида, то есть основания ожидать, что  .
.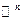 .
. , поэтому
, поэтому
 ,
,
 .
. . Для этого рассмотрим векторы стандартного базиса
. Для этого рассмотрим векторы стандартного базиса 
 . Векторы
. Векторы  не принадлежат
не принадлежат 
 . Рассмотрим систему векторов
. Рассмотрим систему векторов  . Она образует базис
. Она образует базис  , то и
, то и  поэтому следует ожидать, что
поэтому следует ожидать, что  , где
, где  - наибольшее четное число, не превышающее
- наибольшее четное число, не превышающее  (
( , если
, если  , если
, если  (
( ).
).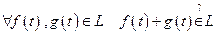 .
. , тогда
, тогда ,
, .
.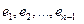 последнего нуля числом (-1) дает нам векторы из
последнего нуля числом (-1) дает нам векторы из 
 и, следовательно,
и, следовательно,  .
.
 - неотрицательная квадратичная форма от
- неотрицательная квадратичная форма от  =0 образуют
=0 образуют  мерное линейное подпространство пространства
мерное линейное подпространство пространства 
 , никак не указывают на способ решения задачи.
, никак не указывают на способ решения задачи. (1)
(1) , (2)
, (2)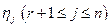 - произвольные числа из
- произвольные числа из  . Имеющийся опыт (задача 1.2) подсказывает, что множество векторов такого вида есть (
. Имеющийся опыт (задача 1.2) подсказывает, что множество векторов такого вида есть ( )-мерное подпространство пространства
)-мерное подпространство пространства  , приводящее форму
, приводящее форму 
 состоит из векторов
состоит из векторов  где
где  , то есть из векторов
, то есть из векторов
 .
. =0 есть линейная оболочка системы векторов
=0 есть линейная оболочка системы векторов 
 .
.

 . Получаем
. Получаем  . Мы пришли к матричному уравнению, которое имеет единственное решение, так как матрица
. Мы пришли к матричному уравнению, которое имеет единственное решение, так как матрица  является невырожденной.
является невырожденной. .
. . Тем самым мы показали, что система
. Тем самым мы показали, что система 



