
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Образ, ядро линейного оператора.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Образом линейного оператора Если Ядро линейного оператора
Задача 3.2. Найти образ, ядро, ранг и дефект оператора Решение. Будем считать, что мы уже убедились в линейности оператора Вычисление образа. Возьмем стандартный базис пространства
(подпространство одномерное).
Вычисление ядра. Пусть Отсюда (В нашем примере Как правило, нахождение ядра в конце концов сводится к решению системы линейных однородных уравнений относительно координат произвольного вектора ядра. В рассмотренном нами примере эта система оказалась очень простой
что позволило нам сразу записать общее решение
Матрица линейного оператора в данных базисах.
Обязательно нужно научиться строить матрицу линейного оператора в данных базисах. Но кроме этого, еще раз обратим наше внимание на следующую теорему: каждый линейный оператор из
Задача 3.3. Для каждого из нижеперечисленных условий постройте пример линейного оператора
Решение. 1. Возьмем какой-либо базис в
Так как
Этими условиями линейный оператор Если
Легко убеждаемся, что Действительно,
6. Так как необходимо построить такой линейный оператор
Можно проверить, что таким образом введенный операторм является линейным и удовлетворяет всем необходимым условиям.
Собственные векторы и собственные значения. Процедура вычисления собственных значений и собственных векторов (собственных подпространств) линейного оператора Задача 3.4. Найдите собственные значения и собственные подпространства оператора
Решение. 1) Строим матрицу оператора
2) Составляем характеристическую матрицу
Оба корня принадлежат полю 3) Составляем систему линейных однородных уравнений с матрицей
Система ранга 2. Множество ее решений - одномерное пространство, линейно независимых решений. Легко находим ее фундаментальную систему решений -
4) Составляем систему линейных однородных уравнений с матрицей
Система ранга 2. Множество ее решений также является одномерным пространством. Легко находим ФСР -
Задача решена.
Замечание 1. Если оператор Замечание 2. Если в процессе решения получилась несовместная система, то допущена ошибка (неверно вычислен характеристический многочлен, найденное Замечание 3. Полезно помнить, что размерность собственного подпространства, относящегося к собственному значению
Замечание 4. В учебных примерах, как правило, корни характеристического многочлена вычисляются точно. На практике часто приходится довольствоваться их приближениями. Возникающие при этом проблемы достаточно сложны и здесь не обсуждаются.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 3179; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.195.178 (0.01 с.) |

 называется множество всех векторов вида
называется множество всех векторов вида 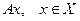 . Если
. Если  , то образ
, то образ  . Его обозначают
. Его обозначают  или
или  .
. , где
, где  - какой-либо базис пространства
- какой-либо базис пространства  .
. , для которых
, для которых  . Ядро линейного оператора (обозначается
. Ядро линейного оператора (обозначается 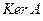 ) – подпространство пространства
) – подпространство пространства 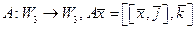 (оператор двойного векторного умножения).
(оператор двойного векторного умножения). :
:  . Находим
. Находим
 .
.
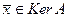 . Это означает, что
. Это означает, что  или
или 
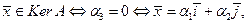 где
где  . Другими словами
. Другими словами  , а дефект
, а дефект 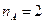 .
. , но это не общее правило). Можно было воспользоваться формулой для двойного векторного произведения. Но решение вряд ли упростилось бы от этого.
, но это не общее правило). Можно было воспользоваться формулой для двойного векторного произведения. Но решение вряд ли упростилось бы от этого.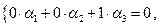
 .
. :
: .
.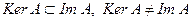 .
. .
. , где
, где  .
.
 .
. переводит в себя, но
переводит в себя, но  , например, стандартный
, например, стандартный .
.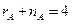 , то из условия
, то из условия  . Для определенности возьмем
. Для определенности возьмем  . Определим
. Определим 
 то по нашему определению
то по нашему определению

 , то есть
, то есть  .
.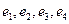 является линейно независимой, а значит, является базисом
является линейно независимой, а значит, является базисом 
 (необходимо самостоятельно проверить линейность)
(необходимо самостоятельно проверить линейность) .
. пространства
пространства  (предполагаем, что линейность оператора проверена):
(предполагаем, что линейность оператора проверена): ,
,  .
. , вычисляем ее определитель и находим корни характеристического многочлена.
, вычисляем ее определитель и находим корни характеристического многочлена. ;
;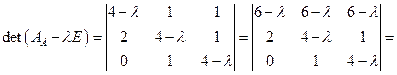


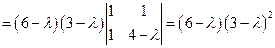 ;
;
 и являются собственными значениями оператора;
и являются собственными значениями оператора;  - кратности 1;
- кратности 1;  - кратности 2.
- кратности 2. и находим ее фундаментальную систему решений:
и находим ее фундаментальную систему решений:
 . Собственное подпространство, относящееся к
. Собственное подпространство, относящееся к 
 и находим ее фундаментальную систему решений:
и находим ее фундаментальную систему решений:
 . Собственное подпространство, относящееся к
. Собственное подпространство, относящееся к 
 не является собственным значением или допущена ошибка в вычислении коэффициентов системы линейных уравнений или в процессе решения системы).
не является собственным значением или допущена ошибка в вычислении коэффициентов системы линейных уравнений или в процессе решения системы).


