
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Канонический корневой базис и жорданова нормальная форма.Содержание книги
Поиск на нашем сайте
Задачи построения канонического корневого базиса (ККБ) и жордановой нормальной формы (ЖНФ) матрицы линейного оператора наиболее сложные, так как 1) большой объем вычислений и 2) приходится опираться на обширный и серьезный теоретический материал. Рассмотрим сначала задачу о построении ККБ. Так как ККБ линейного пространства есть объединение ККБ корневых подпространств данного оператора, то можно предположить, что мы уже выделили корневые подпространства и имеем дело с одним из них - В лекционном курсе ККБ корневого подпространства был построен в виде системы башен убывающей этажности, нижний этаж которых состоял из линейно независимых собственных векторов, а в каждом столбце нижестоящий вектор получался из непосредственно вышестоящего в результате применения оператора
Процедура практического построения ККБ такова: 1. опираясь на какой-либо базис 2. элементарными преобразованиями, сохраняющими башенную структуру, преобразуем систему так, чтобы ее нижний этаж состоял из линейно независимых векторов (этим будет обеспечиваться ЛНЗ всей системы).
Для этого элементарные преобразования будем выполнять сразу над целым столбцом: его перемещение, прибавление к другому столбцу (с меньшей этажностью) и т.п.
Если
Преобразования выполняем слева направо, выбирая их по векторам нижней строки. Рассмотрим конкретный пример. Задача 3.5. Постройте ККБ оператора
Решение. 1) Строим матрицу оператора
Тогда
2) Вычисляем характеристический многочлен оператора и собственные значения:
Пространство 3) Берем произвольный базис (например, стандартный) и к каждому его вектору применяем оператор
Можно сделать некоторые предварительные выводы: максимальная высота корневого вектора равна 3, поэтому в ЖНФ матрицы оператора будет клетка порядка 3 и, следовательно (так как 4-3=1), одна клетка порядка 1. Хотя этого задача не требует, но мы можем написать ЖНФ матрицы оператора:
4) Полагаем
и рассматриваем нижнюю строку. Замечаем: а) третий столбец векторов пропорционален (равен) соответствующей части первого, а четвертый - соответствующей части второго. Выбрасываем без сожаления третий и четвертый столбцы. в) нижний вектор второго столбца пропорционален своему соседу слева. Прибавляем ко второму столбцу первый, умноженный на 1, и получившийся нуль во втором столбце отбрасываем. Таблица примет вид:
Нижняя строка все еще линейно зависима. Ко второму столбцу прибавляем первый, умноженный на 1 (верхний вектор первого столбца, у которого нет соседа справа, в этой операции не участвует), отбрасываем получившийся нуль и приходим к таблице:
Нижняя строка этой таблицы линейно независима, поэтому и вся система векторов линейно независима. Она, занумерованная снизу вверх и слева направо, образует ккб:
Упражнение. Постройте матрицу оператора
ЖНФ матрицы оператора можно отыскать, не выполняя построения ККБ. Число жордановых клеток каждого порядка и максимальный порядок жордановых клеток для каждого собственного значения
( В нашем примере
«Момент» стабилизации ранга Есть клетка третьего порядка (и только одна) и, очевидно, еще одна клетка первого порядка (результат, полученный нами в 3)). Напомним, что в общем случае ( клеток порядка клеток порядка клеток порядка ………………………………………… клеток порядка клеток порядка Следует помнить, что хотя жнф матрицы определена однозначно с точностью до порядка клеток вдоль главной диагонали, ККБ существует бесконечно много. Поэтому не удивительно, если найденный вами ККБ не совпадает с ответом в сборнике задач (но проверить свое решение полезно).
Замечание. Если
Таким образом нами «попутно» найдена преобразующая матрица Е, приводящая данную матрицу
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 427; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.98.111 (0.009 с.) |

 , относящимся к собственному значению
, относящимся к собственному значению  , кратность которого совпадает с
, кратность которого совпадает с 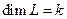 .
.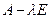 .
.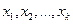 - некоторый базис пространства, то исходная система башен, упорядоченных по высоте, имеет вид:
- некоторый базис пространства, то исходная система башен, упорядоченных по высоте, имеет вид: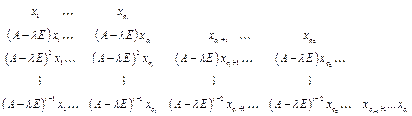

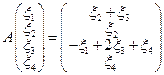 .
. в стандартном базисе
в стандартном базисе 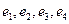 пространства
пространства  . Находим образы базисных векторов:
. Находим образы базисных векторов: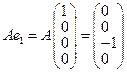 ,
, 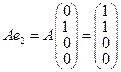 ,
,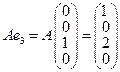
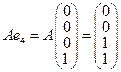 .
.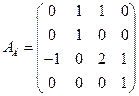 .
.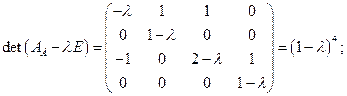
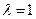 кратности 4.
кратности 4.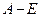 до получения нуля:
до получения нуля: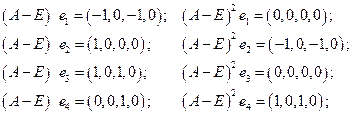
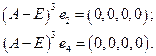
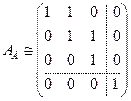 .
.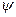
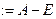 . Выписываем полученные в 3) векторы (кроме нулей, разумеется) в башню:
. Выписываем полученные в 3) векторы (кроме нулей, разумеется) в башню: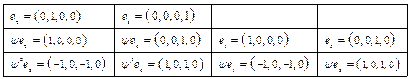
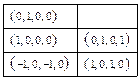 .
.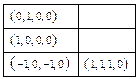 .
.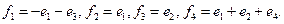
 . Сравните ее с ЖНФ из 3).
. Сравните ее с ЖНФ из 3).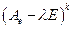
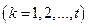 , где
, где 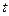 - показатель степени такой, что
- показатель степени такой, что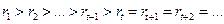
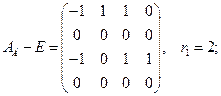
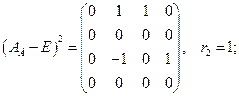
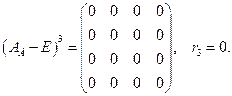
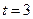 , так как
, так как 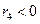 невозможно по определению ранга.
невозможно по определению ранга.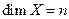 ,
, 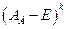 ) число клеток, относящихся к собственному значению
) число клеток, относящихся к собственному значению 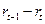 ,
,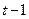 :
: 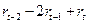 ,
,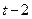 :
: 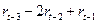 ,
,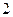 :
: 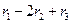 ,
,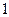 :
: 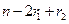 .
.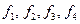 - ККБ оператора
- ККБ оператора  - матрица перехода от базиса
- матрица перехода от базиса 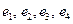 к ККБ, то имеет место равенство:
к ККБ, то имеет место равенство: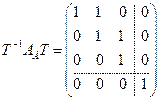 .
.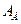 к ЖНФ.
к ЖНФ.


