
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
К-т ф-м н., доц. Савастру О.В.Содержание книги
Поиск на нашем сайте
Рецензенты: д-р ф-м н., проф. Евтухов В.М., К-т ф-м н., доц. Белозеров Г.С.
Рекомендовано к печати Ученым советом ИМЭМ Одесского национального университета им. И. И. Мечникова протокол № 1 от 5 февраля 2008 г. .
СОДЕРЖАНИЕ Обозначения…………………………………………………4 1. Линейные пространства …………………………………...5 1.1. Линейные пространства и подпространства………….5 1.2. Базис пространства, его размерность…………………6 1.3. Координаты вектора в данном базисе…………….…11 1.4. Сумма и пересечение подпространств………………12 2. Евклидовы и унитарные пространства ………….…........17 2.1. Процесс ортогонализации Шмидта………………….17 2.2.Ортогональные дополнения…………………………..19 2.3. Ортогональная проекция и перпендикуляр на подпространство……………………………………………………..20 3. Операторы в линейных пространствах…………….........23 3.1. Образ, ядро линейного оператора……………………28 3.2. Матрица линейного оператора в данных базисах…..29 3.3. Собственные векторы и собственные значения..…...31 3.4. Канонический корневой базис и жорданова нормальная форма…………………………………………………….34 4. Операторы в евклидовых и унитарных пространствах..40 5. Приведение двух квадратичных форм к каноническому виду…………………………………………………………...45 Список литературы………………………………………….51
Линейные пространства и линейные операторы представляют собой начало абстрактной части математики, с которой студенту в дальнейшем неоднократно придется иметь дело. Эти методические указания по самостоятельной работе студентов предполагают использование следующего задачника: И.В.Проскуряков. Сборник задач по линейной алгебре. М., Наука, 1974. ОБОЗНАЧЕНИЯ В дальнейшем мы будем придерживаться следующих обозначений (если в тексте нет специальной оговорки): ¾ ¾ В частности ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾
Основными типами задач этого параграфа являются следующие: А) выяснение вопроса, будет ли данное множество с указанными операциями линейным пространством, подпространством; В) выделение базиса пространства, определение его размерности; С) вычисление координат вектора в данном базисе; D) нахождение суммы, пересечения подпространств, их размерностей и базисов.
Линейные пространства и подпространства. Для решения задач первой группы необходимо знание аксиом линейного пространства (вообще, не следует приниматься за решение задач любого раздела, не ознакомившись предварительно с основными понятиями и теоремами данного раздела). Заметим, что в группе аксиом линейного пространства содержатся требования неограниченной применимости, однозначности и замкнутости линейных операций, которые не выделены под отдельными номерами. Распространенная ошибка: забывают проверить выполнение этих условий. В тех условиях, когда данное множество состоит из векторов некоторого известного пространства, полезной является следующая теорема (критерий подпространства): Теорема. Подмножество 1. 2. Некоторые из задач требуют хорошего знания других разделов курса (элементарной теории матриц, квадратичных форм, систем линейных уравнений). Ниже мы подробнее остановимся на одной из этих задач.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 311; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

 - произвольные пространства над некоторым полем
- произвольные пространства над некоторым полем  ;
;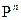 - пространство
- пространство  - мерных строк (столбцов) с элементами из поля
- мерных строк (столбцов) с элементами из поля 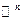 - действительное
- действительное  - комплексное
- комплексное  - пространства геометрических векторов (прямой, плоскости, пространства);
- пространства геометрических векторов (прямой, плоскости, пространства); - евклидовы пространства (с указанием размерности или без него);
- евклидовы пространства (с указанием размерности или без него);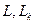 - подпространства данного пространства (
- подпространства данного пространства ( - индекс, не связанный с размерностью);
- индекс, не связанный с размерностью);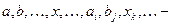 векторы рассматриваемого пространства;
векторы рассматриваемого пространства; 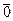 - нулевой вектор;
- нулевой вектор; скаляры из данного поля,
скаляры из данного поля,  - нуль этого поля;
- нуль этого поля; линейные операторы, в отдельных случаях – матрицы;
линейные операторы, в отдельных случаях – матрицы; матрицы линейных операторов в базисах соответственно
матрицы линейных операторов в базисах соответственно  ;
;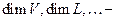 размерности пространств
размерности пространств 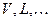 ;
; ранги операторов (матриц)
ранги операторов (матриц) 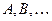 ;
; скалярное произведение в данном пространстве;
скалярное произведение в данном пространстве; векторное произведение в данном пространстве
векторное произведение в данном пространстве 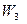 .
. векторов пространства
векторов пространства  над полем
над полем  ,
, .
.


