
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Составители: д-р ф-м н., проф. Варбанец П.Д.,Содержание книги
Поиск на нашем сайте
Линейная алгебра (решение типовых задач) Часть 2 Методические указания для студентов 1 курса Одесса – 2008 Составители: д-р ф-м н., проф. Варбанец П.Д., К-т ф-м н., доц. Савастру О.В.
Рецензенты: д-р ф-м н., проф. Евтухов В.М., К-т ф-м н., доц. Белозеров Г.С.
Рекомендовано к печати Ученым советом ИМЭМ Одесского национального университета им. И. И. Мечникова протокол № 1 от 5 февраля 2008 г. .
СОДЕРЖАНИЕ Обозначения…………………………………………………4 1. Линейные пространства …………………………………...5 1.1. Линейные пространства и подпространства………….5 1.2. Базис пространства, его размерность…………………6 1.3. Координаты вектора в данном базисе…………….…11 1.4. Сумма и пересечение подпространств………………12 2. Евклидовы и унитарные пространства ………….…........17 2.1. Процесс ортогонализации Шмидта………………….17 2.2.Ортогональные дополнения…………………………..19 2.3. Ортогональная проекция и перпендикуляр на подпространство……………………………………………………..20 3. Операторы в линейных пространствах…………….........23 3.1. Образ, ядро линейного оператора……………………28 3.2. Матрица линейного оператора в данных базисах…..29 3.3. Собственные векторы и собственные значения..…...31 3.4. Канонический корневой базис и жорданова нормальная форма…………………………………………………….34 4. Операторы в евклидовых и унитарных пространствах..40 5. Приведение двух квадратичных форм к каноническому виду…………………………………………………………...45 Список литературы………………………………………….51
Линейные пространства и линейные операторы представляют собой начало абстрактной части математики, с которой студенту в дальнейшем неоднократно придется иметь дело. Эти методические указания по самостоятельной работе студентов предполагают использование следующего задачника: И.В.Проскуряков. Сборник задач по линейной алгебре. М., Наука, 1974. ОБОЗНАЧЕНИЯ В дальнейшем мы будем придерживаться следующих обозначений (если в тексте нет специальной оговорки): ¾ ¾ В частности ¾
¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾ ¾
Основными типами задач этого параграфа являются следующие: А) выяснение вопроса, будет ли данное множество с указанными операциями линейным пространством, подпространством; В) выделение базиса пространства, определение его размерности; С) вычисление координат вектора в данном базисе; D) нахождение суммы, пересечения подпространств, их размерностей и базисов.
Координаты вектора в данном базисе. Решение вопроса о ранге системы векторов, заданных координатами в некотором базисе, выделение из системы ее максимальной линейно независимой подсистемы, выражение остальных векторов в виде линейных комбинаций векторов этой подсистемы сводится к решению этих же задач для системы строк (столбцов) координатной матрицы, которые подробно обсуждались в соответствующем параграфе первой части.
ЕВКЛИДОВЫ И УНИТАРНЫЕ ПРОСТРАНСТВА. Основные типы задач этого параграфа: · проверка выполнения аксиом скалярного произведения и доказательство его различных свойств (№№1351-1354, 1384); · ортогонализация данной системы векторов, построение ортогональных и ортонормированных базисов (№№1355-1363); · построение ортогональных дополнений данных подпространств (№№1364-1368); · нахождение ортогональных проекций и перпендикуляров на подпространство (№№1369-1372); · вычисление длин, расстояний, углов (№№1373-1406).
Ортогональные дополнения. Задачи этого раздела не вызовут трудностей, если разобраться в свойствах решений линейной однородной системы как векторов евклидова (унитарного) пространства.
Рассмотрим пространство
Обозначив
Пусть Задача 2.2. Найти базис ортогонального дополнения
Найти уравнения, задающие подпространство Решение. Так как
Находим фундаментальную систему ее решений (ранг системы 2)
Следовательно,
задает подпространство
Аналогичные соображения используются при дополнении ортогональной системы до ортогонального базиса.
Решение. 1.
Все условия выполнены, значит,
5.
Находим
Точно так же
Все условия определения линейного оператора выполнены.
Линейный оператор нулевой вектор отображает в нулевой ( Для доказательства нелинейности достаточно привести пример двух векторов, для которых нарушена аддитивность, или пример вектора или скаляра, для которых не выполнена однородность (равенство
Очевидное неравенство В этом же примере можно поступить и так:
Поэтому оператор Проверку линейности операторов из упражнений 4 и 6 предоставляем читателю.
Чтобы глубже понять определение линейного оператора, придумайте примеры: 1. оператора аддитивного, но не однородного; 2. оператора однородного, но не аддитивного.
Задача решена.
Замечание 1. Если оператор Замечание 2. Если в процессе решения получилась несовместная система, то допущена ошибка (неверно вычислен характеристический многочлен, найденное Замечание 3. Полезно помнить, что размерность собственного подпространства, относящегося к собственному значению
Замечание 4. В учебных примерах, как правило, корни характеристического многочлена вычисляются точно. На практике часто приходится довольствоваться их приближениями. Возникающие при этом проблемы достаточно сложны и здесь не обсуждаются.
Задача решена.
Задача 4.2. В пространстве и задана матрица Построить матрицу Решение. Проверим, является ли базис
Ортогонализируем систему
Осталось нормировать полученную систему
Мы построили ОНБ Матрица перехода от базиса
Мы знаем, как связаны матрицы сопряженных операторов в ОНБ
поэтому
Используя матрицу перехода
Задача решена. Решение. Перепишем формы Так как Оно удовлетворяет всем аксиомам скалярного произведения (положительная определенность формы необходима для выполнения аксиомы 4, а именно Рассмотрим стандартный базис в Используя введенное скалярное произведение, ортогонализируем его:
Нормируем вектора
Матрица перехода от старого базиса к новому задает матрицу
Действительно,
Аналогично,
Далее используем метод приведения квадратичной формы к главным осям. Характеристический многочлен
Теперь составляем ортогональную матрицу, столбцами которой являются векторы
Тогда матрица
и будет искомой матрицей невырожденного линейного преобразования переменных
приводящего формы
Задача решена.
Список литературы
1. Завало С.Т., Костарчук В.Н., Хацет Б.И. Алгебра и теория чисел, ч.1. – К.: Вища школа, 1980. 2. Кострикин А. И. Введение в алгебру. - М.: Наука, 1977. 3. Курош А.Г. Курс высшей алгебры. – М.: Наука, 1975. 4. Проскуряков. Сборник задач по линейной алгебре. М., Наука, 1974.
Линейная алгебра (решение типовых задач) Часть 2 Методические указания для студентов 1 курса Одесса – 2008 Составители: д-р ф-м н., проф. Варбанец П.Д.,
|
||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.223.191 (0.012 с.) |

 - произвольные пространства над некоторым полем
- произвольные пространства над некоторым полем  ;
;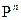 - пространство
- пространство  - мерных строк (столбцов) с элементами из поля
- мерных строк (столбцов) с элементами из поля 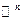 - действительное
- действительное  - комплексное
- комплексное  - пространства геометрических векторов (прямой, плоскости, пространства);
- пространства геометрических векторов (прямой, плоскости, пространства); - евклидовы пространства (с указанием размерности или без него);
- евклидовы пространства (с указанием размерности или без него);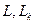 - подпространства данного пространства (
- подпространства данного пространства ( - индекс, не связанный с размерностью);
- индекс, не связанный с размерностью);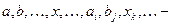 векторы рассматриваемого пространства;
векторы рассматриваемого пространства; 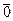 - нулевой вектор;
- нулевой вектор; скаляры из данного поля,
скаляры из данного поля,  - нуль этого поля;
- нуль этого поля; линейные операторы, в отдельных случаях – матрицы;
линейные операторы, в отдельных случаях – матрицы; матрицы линейных операторов в базисах соответственно
матрицы линейных операторов в базисах соответственно  ;
;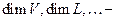 размерности пространств
размерности пространств 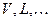 ;
; ранги операторов (матриц)
ранги операторов (матриц) 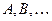 ;
; скалярное произведение в данном пространстве;
скалярное произведение в данном пространстве; векторное произведение в данном пространстве
векторное произведение в данном пространстве 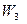 .
. :
: (4)
(4) и
и  , перепишем систему (4) в виде
, перепишем систему (4) в виде (5)
(5) . Тогда уравнения (5) означают, что
. Тогда уравнения (5) означают, что  и, следовательно,
и, следовательно,  , а каждый вектор из
, а каждый вектор из  является решением системы (4). Итак, множество решений системы (4) и линейная оболочка ее строк коэффициентов являются ортогональными дополнениями друг для друга в пространстве
является решением системы (4). Итак, множество решений системы (4) и линейная оболочка ее строк коэффициентов являются ортогональными дополнениями друг для друга в пространстве  , натянутого на векторы:
, натянутого на векторы: .
. , то
, то 
 .
. , а система уравнений со строками коэффициентов
, а система уравнений со строками коэффициентов  и
и 

 и
и  ).
). является отображением. Проверим аддитивность и однородность.
является отображением. Проверим аддитивность и однородность.

 .
. .
. является линейным оператором.
является линейным оператором. .
.
 ,
, .
.
 .
. . Теперь проверяем аддитивность и однородность. Напомним: если
. Теперь проверяем аддитивность и однородность. Напомним: если  , то
, то  и
и  .
.

 .
.
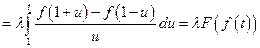 .
. - линейный оператор.
- линейный оператор. ). Поэтому, если
). Поэтому, если  , то
, то  - нелинейный. В упражнении 3
- нелинейный. В упражнении 3  - нелинейный.
- нелинейный. может иметь место и для нелинейных операторов). Например: в упражнении 7 настораживает то, что текущий вектор
может иметь место и для нелинейных операторов). Например: в упражнении 7 настораживает то, что текущий вектор  находится под знаком
находится под знаком  . Поэтому проверку ведем на конкретных векторах.
. Поэтому проверку ведем на конкретных векторах.
 доказывает неаддитивность
доказывает неаддитивность  и его нелинейность.
и его нелинейность.
 не является собственным значением или допущена ошибка в вычислении коэффициентов системы линейных уравнений или в процессе решения системы).
не является собственным значением или допущена ошибка в вычислении коэффициентов системы линейных уравнений или в процессе решения системы). введено скалярное произведение
введено скалярное произведение 
 линейного оператора
линейного оператора  в базисе
в базисе  .
. сопряженного оператора
сопряженного оператора  в базисе
в базисе 
 ,
,  ,
, ,
,  ,
,  .
. .
. ,
,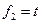 ,
, ,
,  ,
, .
. ,
, ,
, .
. . Теперь мы должны, используя матрицу перехода от одного базиса к другому, перейти к матрице оператора в ОНБ. Зная, как связаны матрицы сопряженных операторов в ОНБ, можно построить матрицу сопряженного оператора
. Теперь мы должны, используя матрицу перехода от одного базиса к другому, перейти к матрице оператора в ОНБ. Зная, как связаны матрицы сопряженных операторов в ОНБ, можно построить матрицу сопряженного оператора  ,
,  .
. .
. ,
, .
. , возвращаемся к исходному базису
, возвращаемся к исходному базису  .
. и
и  в виде
в виде  и
и  , где
, где  ,
,  - матрицы соответствующих квадратичных форм.
- матрицы соответствующих квадратичных форм.

 , то согласно критерию Сильвестра, форма
, то согласно критерию Сильвестра, форма  скалярное произведение
скалярное произведение  .
.
 ).
).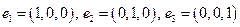 .
.
 и получаем ОНБ в
и получаем ОНБ в 
 квадратичных форм
квадратичных форм  .
.


 .
.

 имеет три корня
имеет три корня  , которым соответствуют следующие собственные вектора:
, которым соответствуют следующие собственные вектора: 
 . Они являются попарно ортогональными, так как соответствуют разным собственным значениям, и образуют собственный ортогональный базис. Осталось его пронормировать:
. Они являются попарно ортогональными, так как соответствуют разным собственным значениям, и образуют собственный ортогональный базис. Осталось его пронормировать:
 .
. ,
, 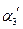 ,
, .
.

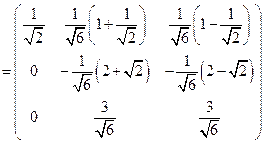

 ,
, .
.


