
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Операторы в евклидовых и унитарных пространствахСодержание книги
Поиск на нашем сайте
Пусть
Для всякого оператора
где Равенство (9) можно применять за определение сопряженного оператора. Матрица Заметим, что в любых ОНБ унитарных пространств Если мы рассматриваем евклидовы пространства
Задача 4.1. Найтисопряженный оператор для оператора
В
Решение. В заданном унитарном пространстве
Итак, искомый сопряженный оператор имеет вид
Задача решена.
Задача 4.2. В пространстве и задана матрица Построить матрицу Решение. Проверим, является ли базис
Ортогонализируем систему
Осталось нормировать полученную систему
Мы построили ОНБ Матрица перехода от базиса
Мы знаем, как связаны матрицы сопряженных операторов в ОНБ
поэтому
Используя матрицу перехода
Задача решена. ПРИВЕДЕНИЕ ДВУХ КВАДРАТИЧНЫХ ФОРМ К КАНОНИЧЕСКОМУ ВИДУ Рассмотрим две вещественные квадратичные формы
Итак, результирующим преобразованием, которое приведет обе квадратичные формы к каноническому виду, причем положительно определенную представит в виде суммы квадратов, будет
Задача 5.1. Для заданной пары квадратичных форм найти невырожденное линейное преобразование, которое приводит эти формы к каноническому виду.
Решение. Перепишем формы Так как Оно удовлетворяет всем аксиомам скалярного произведения (положительная определенность формы необходима для выполнения аксиомы 4, а именно Рассмотрим стандартный базис в Используя введенное скалярное произведение, ортогонализируем его:
Нормируем вектора
Матрица перехода от старого базиса к новому задает матрицу
Действительно,
Аналогично,
Далее используем метод приведения квадратичной формы к главным осям. Характеристический многочлен
Теперь составляем ортогональную матрицу, столбцами которой являются векторы
Тогда матрица
и будет искомой матрицей невырожденного линейного преобразования переменных
приводящего формы
Задача решена.
Список литературы
1. Завало С.Т., Костарчук В.Н., Хацет Б.И. Алгебра и теория чисел, ч.1. – К.: Вища школа, 1980. 2. Кострикин А. И. Введение в алгебру. - М.: Наука, 1977. 3. Курош А.Г. Курс высшей алгебры. – М.: Наука, 1975. 4. Проскуряков. Сборник задач по линейной алгебре. М., Наука, 1974.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 252; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.247.133 (0.01 с.) |

 и
и  - два произвольных пространства, оба евклидовых или оба унитарных. Рассмотрим линейный оператор
- два произвольных пространства, оба евклидовых или оба унитарных. Рассмотрим линейный оператор  . Напомним, что оператор
. Напомним, что оператор  называется сопряженным по отношению к оператору
называется сопряженным по отношению к оператору  , если
, если  и
и  выполняется равенство
выполняется равенство .
. существует и единственный. Причем
существует и единственный. Причем , (9)
, (9) - какой-либо ортонормированный базис (ОНБ)
- какой-либо ортонормированный базис (ОНБ)  с элементами
с элементами  называется сопряженной по отношению к матрице
называется сопряженной по отношению к матрице 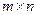 с элементами
с элементами  , если
, если  .
.
 .
. введено естественное скалярное произведение
введено естественное скалярное произведение .
. является ОНБ. Для построения сопряженного оператора воспользуемся равенством (9).
является ОНБ. Для построения сопряженного оператора воспользуемся равенством (9). ,
, ,
, ,
,
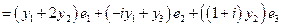 .
. .
. введено скалярное произведение
введено скалярное произведение 
 линейного оператора
линейного оператора  в базисе
в базисе  .
. сопряженного оператора
сопряженного оператора  в базисе
в базисе 
 ,
,  ,
, ,
,  ,
,  .
. .
. ,
,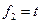 ,
, ,
,  ,
, .
. ,
, ,
, .
. . Теперь мы должны, используя матрицу перехода от одного базиса к другому, перейти к матрице оператора в ОНБ. Зная, как связаны матрицы сопряженных операторов в ОНБ, можно построить матрицу сопряженного оператора
. Теперь мы должны, используя матрицу перехода от одного базиса к другому, перейти к матрице оператора в ОНБ. Зная, как связаны матрицы сопряженных операторов в ОНБ, можно построить матрицу сопряженного оператора  , а затем вернуться опять к исходному базису.
, а затем вернуться опять к исходному базису. ,
,  .
. .
. ,
, .
. , возвращаемся к исходному базису
, возвращаемся к исходному базису  .
. и
и  . Можно ли заданные формы единым преобразованием привести к каноническому виду? Эту задачу помогают решить результаты, относящиеся к линейным операторам. Мы рассмотрим случай, когда одна из этих квадратичных форм, например
. Можно ли заданные формы единым преобразованием привести к каноническому виду? Эту задачу помогают решить результаты, относящиеся к линейным операторам. Мы рассмотрим случай, когда одна из этих квадратичных форм, например  , является положительно определенной. Тогда выполняем сначала преобразование
, является положительно определенной. Тогда выполняем сначала преобразование  , которое приводит форму
, которое приводит форму  перейдет в новую форму от переменных
перейдет в новую форму от переменных  . На следующем шаге выполняется ортогональное преобразование
. На следующем шаге выполняется ортогональное преобразование  , которое приводит форму
, которое приводит форму  .
. .
.
 и
и  , где
, где  ,
,  - матрицы соответствующих квадратичных форм.
- матрицы соответствующих квадратичных форм.

 , то согласно критерию Сильвестра, форма
, то согласно критерию Сильвестра, форма  .
.
 ).
).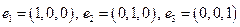 .
.
 и получаем ОНБ в
и получаем ОНБ в 
 невырожденного преобразования переменных
невырожденного преобразования переменных  .
.


 .
.

 имеет три корня
имеет три корня  , которым соответствуют следующие собственные вектора:
, которым соответствуют следующие собственные вектора: 
 . Они являются попарно ортогональными, так как соответствуют разным собственным значениям, и образуют собственный ортогональный базис. Осталось его пронормировать:
. Они являются попарно ортогональными, так как соответствуют разным собственным значениям, и образуют собственный ортогональный базис. Осталось его пронормировать:
 .
. ,
, 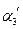 ,
, .
.

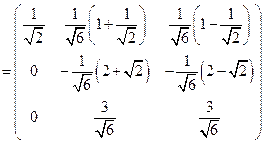

 ,
, .
.


