
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ортогональная проекция и перпендикуляр на подпространство.Содержание книги
Поиск на нашем сайте
Известно, что
и потому каждый вектор
где
Если
и тогда
Умножаем последнее равенство скалярно на
Эта система в силу существования представления (7) совместна. Определитель матрицы этой системы есть определитель Грама
Умение находить Задача 2.3. Вычислить расстояние от вектора
Решение. Напомним: плоскостью (линейным многообразием) называется множество векторов вида
где
Расстояние от вектора Так как
(применена теорема Пифагора), то
Мы получили формулу Остается вычислить
и тогда
Умножаем последнее равенство скалярно на
Решая систему, находим Тогда
ОПЕРАТОРЫ В ЛИНЕЙНЫХ ПРОСТРАНСТВАХ. Пусть
Образ вектора Оператор
1. (аддитивность оператора); 2. (однородность оператора). Понятие линейного оператора является одним из важнейших в математике. Это подтверждается хотя бы тем, что основные операторы, изучаемые в математическом анализе и алгебре (предельный переход, дифференцирование, интегрирование, проектирование на подпространство, умножение на матрицу и др.) являются линейными. Оператор Основные типы задач по этой теме: a) проверка линейности заданного оператора; b) нахождение образа, ядра, ранга и дефекта линейного оператора; c) построение матрицы линейного оператора в данных базисах (в данном базисе); d) нахождение собственных значений и собственных векторов линейного оператора (№№1465-1484); e) построение канонического базиса и жордановой нормальной формы линейного оператора (№№1529-1536).
Основная трудность задач первой группы состоит в том, что примеры операторов могут быть взяты из различных разделов математики и требуют от студента эрудиции и определенной математической культуры. Приведем несколько примеров.
Задача 3.1. Проверьте линейность следующих операторов: 1. 2.
3. 4. 5. 6. 7. Решение. 1.
Все условия выполнены, значит,
5.
Находим
Точно так же
Все условия определения линейного оператора выполнены.
Линейный оператор нулевой вектор отображает в нулевой ( Для доказательства нелинейности достаточно привести пример двух векторов, для которых нарушена аддитивность, или пример вектора или скаляра, для которых не выполнена однородность (равенство
Очевидное неравенство В этом же примере можно поступить и так:
Поэтому оператор Проверку линейности операторов из упражнений 4 и 6 предоставляем читателю.
Чтобы глубже понять определение линейного оператора, придумайте примеры: 1. оператора аддитивного, но не однородного; 2. оператора однородного, но не аддитивного.
|
||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.157.13 (0.01 с.) |

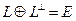 ,
,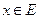 единственным способом представим в виде суммы
единственным способом представим в виде суммы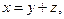
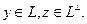 Вектор
Вектор 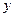 называют (ортогональной) проекцией вектора
называют (ортогональной) проекцией вектора 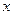 на подпространство
на подпространство  и обозначают
и обозначают 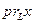 , а
, а 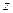 - перпендикуляром (ортогональной составляющей) из вектора
- перпендикуляром (ортогональной составляющей) из вектора 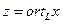 . Очевидно, что
. Очевидно, что ,
, 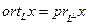 . (6)
. (6)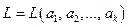 , то
, то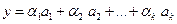 (7)
(7)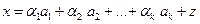 .
.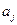 ,
, 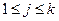 , с учетом
, с учетом 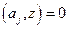 , получаем
, получаем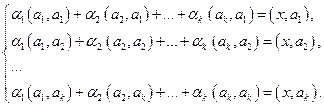 (8)
(8)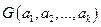 . Если
. Если 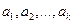 - линейно независима, то
- линейно независима, то 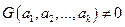 и система (8) имеет единственное решение. В противном случае у системы (8) решений бесконечно много. Но нам достаточно найти одно (все другие решения дадут нам те же векторы
и система (8) имеет единственное решение. В противном случае у системы (8) решений бесконечно много. Но нам достаточно найти одно (все другие решения дадут нам те же векторы  и если, опираясь на соотношения (6), выбрать то подпространство, размерность которого меньше.
и если, опираясь на соотношения (6), выбрать то подпространство, размерность которого меньше.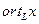 позволит успешно справиться с большинством задач на вычисление длин, расстояний и углов.
позволит успешно справиться с большинством задач на вычисление длин, расстояний и углов.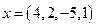 до плоскости
до плоскости 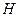 , заданной системой уравнений
, заданной системой уравнений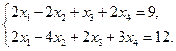 .
.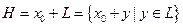 ,
,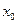 - вектор сдвига,
- вектор сдвига, 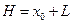 , где
, где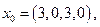
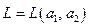 ,
,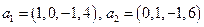 .
.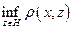 или как
или как 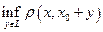 .
.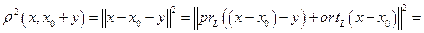
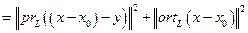
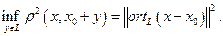
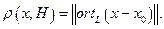
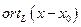 и его длину.
и его длину. 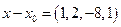 .
.
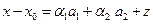 .
.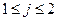 , с учетом
, с учетом 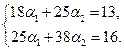
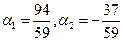 .
.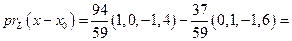
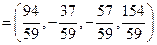 .
.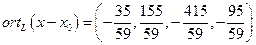 .
.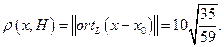
 и
и  - два произвольных линейных пространства. Как известно, оператором, действующим из
- два произвольных линейных пространства. Как известно, оператором, действующим из  , то это записывают так:
, то это записывают так: .
.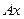 или
или 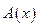 и называют значением оператора
и называют значением оператора 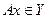 .
. и при этом
и при этом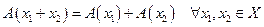
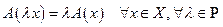
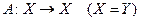 называют также преобразованием пространства
называют также преобразованием пространства 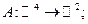
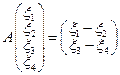 .
.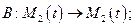 (
(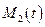 -пространство многочленов степени
-пространство многочленов степени 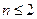 над некоторым полем).
над некоторым полем).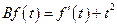 .
.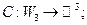
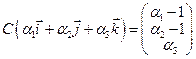 .
.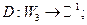
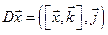 .
.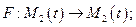
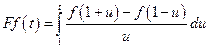 .
.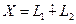 . Определим оператор
. Определим оператор 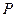 так: если
так: если  и
и 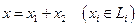 , то
, то 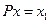 (оператор проектирования на
(оператор проектирования на 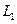 параллельно
параллельно 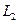 ).
).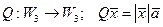 (
(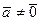 - фиксированный вектор).
- фиксированный вектор). является отображением. Проверим аддитивность и однородность.
является отображением. Проверим аддитивность и однородность.

 .
. .
. .
.
 ,
, .
.
 .
. . Теперь проверяем аддитивность и однородность. Напомним: если
. Теперь проверяем аддитивность и однородность. Напомним: если  , то
, то  и
и  .
.

 .
.
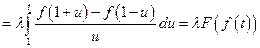 .
. - линейный оператор.
- линейный оператор. ). Поэтому, если
). Поэтому, если  , то
, то  - нелинейный. В упражнении 3
- нелинейный. В упражнении 3  - нелинейный.
- нелинейный. может иметь место и для нелинейных операторов). Например: в упражнении 7 настораживает то, что текущий вектор
может иметь место и для нелинейных операторов). Например: в упражнении 7 настораживает то, что текущий вектор  находится под знаком
находится под знаком  . Поэтому проверку ведем на конкретных векторах.
. Поэтому проверку ведем на конкретных векторах.
 доказывает неаддитивность
доказывает неаддитивность  и его нелинейность.
и его нелинейность.



