
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экономико-математические модели задач линейного программирования. Геометрическая интерпретация злп.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
К задачам оптимизации относятся задачи на отыскание —целевой функции + максимума или минимума целевой функции —решения системы уравнений — решения системы неравенств
Критерием оптимальности задачи математического программирования является +целевая функция —система уравнений —система неравенств —условие неотрицательности переменных
Общая задача линейного программирования имеет вид — — —
+
Задача математического программирования является задачей линейного программирования, если —целевая функция является линейной, а система ограничений нелинейная —система ограничений – это система линейных уравнений или неравенств, а целевая функция нелинейная +целевая функция является линейной, а система ограничений – система линейных уравнений или неравенств —условие неотрицательности переменных - линейно
Задача математического программирования является задачей нелинейного программирования, если —условие неотрицательности переменных нелинейно + целевая функция является нелинейной —целевая функция является линейной — условие неотрицательности переменных не выполняется
Задача нелинейного программирования называется квадратичной, если — — + —
Задача нелинейного программирования называется задачей дробно – линейного программирования, если — — — +
Задача математического программирования называется задачей целочисленного программирования, если —все коэффициенты целевой функции – целые числа —все коэффициенты системы ограничений – целые числа —все +все
Абстрактное отображение реального экономического процесса с помощью математических выражений, уравнений, неравенств – это —система ограничений — целевая функция +экономико–математическая модель —условие неотрицательных переменных
Любая экономико – математическая модель задачи линейного программирования состоит из —целевой функции и системы ограничений +целевой функции, системы ограничений и условия неотрицательности переменных —системы ограничений и условия неотрицательности переменных — целевой функции и условия неотрицательности переменных
Задача математического программирования называется задачей сепарабельного программирования, если целевая функция + — — —
Оптимальное решение задачи математического программирования – это — допустимое решение системы ограничений —любое решение системы ограничений +допустимое решение системы ограничений, приводящее к максимуму или минимуму целевой функции —максимальное или минимальное решение системы ограничений
Если целевая функция —линейного программирования — целочисленного программирования —дробно – линейного программирования +квадратичного программирования
Динамическое программирование – это математический аппарат, позволяющий + осуществить оптимальное планирование многошаговых управляемых процессов —исследовать динамику функции —оказывать влияние на развитие процесса —наблюдать процесс в его развитии
Если целевая функция —линейного программирования — квадратичного программирования +дробно – линейного программирования — дробно – квадратичного программирования
Все ограничения в задаче математического программирования должны быть — одинакового смысла —противоречивы +непротиворечивы —противоположного смысла
Задачи линейного программирования предполагают —минимальные ресурсы — максимальные ресурсы —неограниченные ресурсы +ограниченные ресурсы
В задаче об оптимальном распределении ресурсов критерием оптимальности является +максимальная прибыль —минимальная прибыль —максимальные издержки —минимальные издержки
В задаче «о диете» критерием оптимальности является —максимальная прибыль — минимальная прибыль —максимальная стоимость рациона питания +минимальная стоимость рациона питания
Задачи об оптимальном распределении ресурсов и «о диете» относятся к задачам +линейного программирования —нелинейного программирования — динамического программирования —целочисленного программирования
Система ограничений называется стандартной, если она содержит все знаки —³ +£ —= —¹
Задача линейного программирования решается графическим способом, если в задаче —одна переменная +две переменные —три переменные —четыре переменные
Неравенство вида —прямую —окружность +полуплоскость —плоскость
Областью допустимых решений ЗЛП является —вся плоскость —круг +выпуклый многоугольник —координатные оси
Максимум или минимум целевой функции находится —в начале координат —на сторонах выпуклого многоугольника решений —внутри выпуклого многоугольника решений +в вершинах выпуклого многоугольника решений
Каноничкеским видом ЗЛП называется такой ее вид, в котором система ограничений содержит знаки —³ — £ += —¹
Для приведения ЗЛП к каноническому виду вводятся +дополнительные переменные —искусственные переменные —отрицательные переменные —нулевые переменные
Если ограничение задано со знаком «³», то дополнительная переменная вводится в это ограничение с коэффициентом —+1 +-1 —0 —М
Если ограничение задано со знаком «£», то дополнительная переменная вводится в это ограничение с коэффициентом ++1 —-1 —0 —М
В целевую функцию дополнительные переменные вводятся с коэффициентами — +1 —-1 +0 —M
В задаче об оптимальном распределении ресурсов дополнительная переменная —прибыль от реализации продукции i –го вида —прибыль от реализации 1 единицы продукции i – го вида —использованные ресурсы i – го вида +неиспользованные ресурсы i –го вида
В задаче об оптимальном распределении ресурсов коэффициент —прибыль от реализации продукции j – го вида + прибыль от реализации 1 единицы продукции j– го вида —количество продукции j – го вида —расход сырья для производства продукции j – го вида
В задаче об оптимальном распределении ресурсов переменная —прибыль от реализации продукции j – го вида — прибыль от реализации 1 единицы продукции j– го вида +количество продукции j – го вида —расход сырья для производства продукции j – го вида
В задаче «о диете» коэффициент +цена 1 единицы продукта j– го вида — расход продукта j – го вида — прибыль от использования продукта j– го вида — прибыль от реализации продукта j– го вида
В задаче «о диете» коэффициент +содержание питательного вещества с номером i в 1 единице j – го продукта —цена 1 единицы продукта j– го вида —количество j – го продукта, необходимого i – му животному —издержки на приобретение j – го продукта для прокорма i – го животного
В задаче об оптимальном распределении ресурсов коэффициент +количество ресурса с номером —неиспользованные ресурсы i - го вида —прибыль от реализации 1 единицы продукции j – го вида —количество продукции j – го вида
В задаче об оптимальном распределении ресурсов требование неотрицательности накладывается на —только основные переменные +на основные и дополнительные переменные —только на дополнительные переменные —первую и вторую переменные
В задаче о «диете» область допустимых решений —ограничена —незамкнута +неограничена —невыпукла
Динамическое программирование основано на решении —вероятностного уравнения —дифференциального уравнения —уравнение регрессии +функционального уравнения
В задаче о «диете» в правой части ограничений находятся + необходимое количество питательных веществ каждого вида —стоимость единицы корма j – го вида —количества корма каждого вида —общая стоимость рациона
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 3417; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.28.135 (0.007 с.) |

 (max или min),
(max или min),  ,
, 


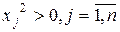

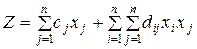





 - целые числа
- целые числа - целые числа,
- целые числа, 
 равна
равна

 , где
, где 

 ,то задача математического программирования является задачей
,то задача математического программирования является задачей описывает
описывает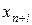 имеет экономический смысл:
имеет экономический смысл: целевой функции
целевой функции  - это
- это - это
- это , необходимого для изготовления 1 единицы продукции j – го вида
, необходимого для изготовления 1 единицы продукции j – го вида


