
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет и задачи исследования операцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте И.Н. Слинкина
Учебное пособие для студентов педагогических вузов по специальности «Информатика»
Шадринск, 2003
Слинкина И.Н. Исследование операций. Учебно-методическое пособие. – Шадринск: изд-во Шадринского государственного педагогического института, 2002. - 106 с.
Слинкина И.Н. – кандидат педагогических наук
В учебном пособии представлена теоретическая часть курса «Исследование операций». Оно предназначено для студентов очного и заочного отделений факультетов, реализующих специальность «Информатика».
© Шадринский государственный педагогический институт © Слинкина И.Н., 2002 Оглавление Вопросы к блокам по курсу «Исследование операций» 5 Блок 1. 7 1.1. Предмет и задачи исследования операций 7 1.2. Основные понятия и принципы исследования операций 8 1.3. Математические модели операций 10 1.4. Понятие линейного программирования 12 1.5. Примеры экономических задач линейного программирования. Задача о наилучшем использовании ресурсов 13 1.6. Примеры экономических задач линейного программирования. Задача о выборе оптимальных технологий 15 1.7. Примеры экономических задач линейного программирования. Задача о смесях 16 1.8. Примеры экономических задач линейного программирования. Транспортная задача 17 1.9. Основные виды записи задач линейного программирования 19 1.10. Способы преобразования 21 1.11. Переход к канонической форме 22 1.12. Переход к симметричной форме записи 25 Блок 2. 28 2.1. Геометрическая интерпретация задачи линейного программирования 28 2.2. Решение задач линейного программирования графическим методом 29 2.3. Свойства решений задачи линейного программирования 34 2.4. Общая идея симплексного метода 35 2.5. Построение начального опорного плана при решении задач линейного программирования симплексным методом 36 2.6. Признак оптимальности опорного плана. Симплексные таблицы 40 2.7. Переход к нехудшему опорному плану. 44 2.8. Симплексные преобразования 46 2.9. Альтернативный оптимум (признак бесконечности множества опорных планов) 51 2.10. Признак неограниченности целевой функции 52 2.11. Понятие о вырождении. Монотонность и конечность симплексного метода. Зацикливание 53 2.12. Понятие двойственности для симметричных задач линейного программирования 54 Блок 3 57 3.1. Несимметричные двойственные задачи 57 3.2. Открытая и закрытая модели транспортной задачи 61 3.3. Построение начального опорного плана. Правило "Северо-западного угла" 63 3.4. Построение начального опорного плана. Правило минимального элемент 64 3.5. Построение начального опорного плана. Метод Фогеля 64 3.6. Метод потенциалов 65 3.7. Решение транспортных задач с ограничениями по пропускной способности 69 3.8. Примеры задач дискретного программирования. Задача о контейнерных перевозках. Задача о назначении 71 3.9. Сущность методов дискретной оптимизации 72 3.10. Задача выпуклого программирования 74 3.11. Метод множителей Лагранжа 75 3.12. Градиентные методы 77 Блок 4 78 4.1. Методы штрафных и барьерных функций 78 4.2. Динамическое программирование. Основные понятия. Сущность методов решения 79 4.3. Стохастическое программирование. Основные понятия 81 4.4. Матричные игры с нулевой суммой 83 4.5. Чистые и смешанные стратегии и их свойства 85 4.6. Свойства чистых и смешанных стратегий 88 4.7. Приведение матричной игры к ЗЛП 92 4.8. Задачи теории массового обслуживания. Классификация систем массового обслуживания 94 4.9. Потоки событий 96 4.10. Схема гибели и размножения 97 4.11. Формула Литтла 99 4.12. Простейшие системы массового обслуживания 101 Список рекомендуемой литературы 106
Вопросы к блокам по курсу «Исследование операций» Блок 1 1. Предмет и задачи исследования операций. 2. Основные понятия и принципы исследования операций. 3. Математические модели операций. 4. Понятие линейного программирования. 5. Примеры экономических задач линейного программирования. Задача о наилучшем использовании ресурсов. 6. Примеры экономических задач линейного программирования. Задача о выборе оптимальных технологий. 7. Примеры экономических задач линейного программирования. Задача о смесях. 8. Примеры экономических задач линейного программирования. Транспортная задача. 9. Основные виды записи задач линейного программирования. 10. Способы преобразования. 11. Переход к канонической форме. 12. Переход к симметричной форме записи.
Блок 2 1. Геометрическая интерпретация задачи линейного программирования. 2. Решение задач линейного программирования графическим методом. 3. Свойства решений задачи линейного программирования. 4. Общая идея симплексного метода. 5. Построение начального опорного плана при решении задач линейного программирования симплексным методом. 6. Признак оптимальности опорного плана. Симплексные таблицы. 7. Переход к нехудшему опорному плану. 8. Симплексные преобразования. 9. Альтернативный оптимум (признак бесконечности множества опорных планов). 10. Признак неограниченности целевой функции. 11. Понятие о вырождении. Монотонность и конечность симплексного метода. Зацикливание. 12. Понятие двойственности для симметричных задач линейного программирования.
Блок 3 1. Несимметричные двойственные задачи. 2. Открытая и закрытая модели транспортной задачи. 3. Построение начального опорного плана. Правило "Северо-западного угла". 4. Построение начального опорного плана. Правило минимального элемент. 5. Построение начального опорного плана. Метод Фогеля. 6. Метод потенциалов. 7. Решение транспортных задач с ограничениями по пропускной способности. 8. Примеры задач дискретного программирования. Задача о контейнерных перевозках. Задача о назначении. 9. Сущность методов дискретной оптимизации. 10. Задача выпуклого программирования. 11. Метод множителей Лагранжа. 12. Градиентные методы.
Блок 4 1. Метод штрафных и барьерных функций. 2. Динамическое программирование. Основные понятия. Сущность методов решения. 3. Стохастическое программирование. Основные понятия. 4. Матричные игры с нулевой суммой. 5. Чистые и смешанные стратегии. 6. Свойства чистых и смешанных стратегий. 7. Приведение матричной игры к ЗЛП 8. Задачи теории массового обслуживания. Классификация систем массового обслуживания. 9. Потоки событий. 10. Схема гибели и размножения. 11. Формула Литтла. 12. Простейшие системы массового обслуживания. Блок 1. Основные понятия и принципы исследования операций
Определение: Операцией называется всякое мероприятие (система действий), объединенное единым замыслом и направленное к достижению какой-то цели. Операция есть всегда управляемое мероприятие, т.е. от расчетов зависит, каким способом выбрать параметры, характеризующие ее организацию. «Организация» здесь понимается в широком смысле слова, включая набор технических средств, применяемых в операции. Определение: Всякий определенный выбор зависящий от решающих параметров называется решением. Определение: Оптимальными называются решения, по тем или иным причинам предпочтительные перед другими. Цель исследования операций – предварительное количественное обоснование оптимальных решений. Иногда в результате исследования удается указать одно-единственное строго определенное решение, гораздо чаще – выделить область практически равноценных оптимальных решений, в пределах которой может быть сделан конечный выбор. Само принятие решений выходит за рамки исследования операций и относится к компетенции ответственного лица, чаще – группы лиц, которым представляется право окончательного выбора и на которых возложена ответственность за этот выбор. Определение: Параметры, совокупность которых образует решение, называются элементами решения. В качестве элементов решения могут фигурировать различные числа, векторы, функции, физические признаки и т.д. Для упрощения всю совокупность элементов решения будем обозначать х.
Чтобы сравнивать между собой по эффективности разные решения, нужно иметь какой-то количественный критерий, так называемый показатель эффективности (целевая функция). Этот показатель выбирается так, чтобы он отражал целевую направленность операции. Лучшим будет считаться то решение, которое в максимальной степени способствует достижению поставленной цели. Чтобы выбрать показатель эффективности Z, нужно прежде всего определить, к чему должно привести решение задачи. Выбирая решение, предпочтение отдается такому, которое обращает показатель эффективности Z в максимум или в минимум. Например, доход от операции хотелось бы обратить в максимум; если же показателем эффективности являются затраты, их желательно обратить в минимум. Очень часто выполнение операции сопровождается действием случайных факторов: «капризов» природы, колебания спроса и предложения, отказы технических устройств и т.д. В таких случаях обычно в качестве показателя эффективности берется не сама величина, которую хотелось бы максимизировать (минимизировать), а среднее значение (математическое ожидание). Задача выбора показателя эффективности решается для каждой проблемы индивидуально. Задача 1. О наилучшем использовании ресурсов. Задача операции – произвести максимальное количество товаров. Показатель эффективности Z – прибыль от продажи товаров при минимальных затратах на ресурсы (max Z).
Естественный показатель эффективности, подсказанный формулировкой задачи, - это цена необходимых для смеси продуктов при условии необходимости сохранения заданных свойств смеси(min Z). Задача 3. Транспортная задача. Задача операции – обеспечить снабжение товарами потребителей при минимальных расходах на перевозки. Показатель эффективности Z – суммарные расходы на перевозки товаров за единицу времени (min Z).
Примеры экономических задач линейного программирования. Задача о наилучшем использовании ресурсов
Пусть некоторая производственная единица (цех, завод, объединение и т.д.), исходя из конъюнктуры рынка, технических или технологических возможностей и имеющихся ресурсов может выпускать n различных видов продукции (товаров), известных под номерами, обозначаемыми индексами j
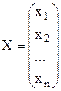
Обозначим через Х= Так как
Это выражение – целевая функция, которую нужно максимизировать. Так как
Чтобы искомый план Х=
Таким образом, модель задачи о наилучшем использовании ресурсов имеет вид: Найти:
при ограничениях
Т.к. переменные
Примеры экономических задач линейного программирования. Задача о выборе оптимальных технологий
В задаче о наилучшем использовании ресурсов определяется оптимальный план выпуска продукции. Пусть при производстве какого-то общественно необходимого продукта используется n технологий. При этом требуется m видов ресурсов, заданных объемами
при ограничениях на лимитируемые ресурсы
и условия неотрицательности
Примеры экономических задач линейного программирования. Задача о смесях
В различных отраслях народного хозяйства возникает проблема составления таких рабочих смесей на основе исходным материалов, которые обеспечивали бы получение конечного продукта, обладающего определенными свойствами. К этой группе относят задачи о выборе диеты, составления кормового рациона в животноводстве, шихт в металлургии, горючих и смазочных смесей в нефтеперерабатывающей промышленности и т.д. Высокий уровень затрат на исходные сырьевые материалы и необходимость повышения эффективности производства выдвигает на первый план следующую задачу: получить продукцию с заданными свойствами при наименьших затратах на исходные сырьевые материалы. Модель задачи о наилучшем составе смеси рассмотрим на примере задачи о диете. Имеются пищевые продукты, известные под номерами 1, 2, 3,..., j,..., n. Они содержат различные питательные вещества, обозначаемые номерами 1, 2, 3,..., i,..., m (углеводы, белки, жиры, витамины, микроэлементы и др.). Единица j-го продукта содержит Математическая модель задачи: Найти:
при ограничениях
Примеры экономических задач линейного программирования. Транспортная задача
Рассмотрим простейший вариант модели транспортной задачи, когда речь идет о рациональной перевозке некоторого однородного продукта от производителей к потребителям, при этом имеется баланс между суммарным спросом потребителей и возможностями поставщиков по их удовлетворению. Причем, потребителям безразлично, из каких пунктов производства будет поступать продукция, лишь бы их заявки были полностью удовлетворены. От схемы прикрепления потребителей к поставщикам существенно зависит объем транспортной работы, возникает задача о наиболее рациональном прикреплении, правильном направлении перевозок грузов, при котором потребности полностью удовлетворяются, вся продукция от поставщиков вывозится, а затраты на транспортировку минимальны. Задача формулируется так: имеется m пунктов производства, в каждом из которых сосредоточено
Известны величины
Матрица Х=||
С целью удобства построения математической модели матрицы тарифов и перевозок совмещают в одну, именуемую макетом транспортной задачи:
Математическая модель транспортной задачи: целевая функция, описывающая транспортные затраты,
минимизируется при ограничениях на возможности поставщиков: весь продукт из пункта производства должен быть вывезен:
на спрос потребителей, который должен быть удовлетворен:
при условии неотрицательности переменных, исключающем обратные перевозки
Определение: Общей задачей линейного программирования называют задачу:
при ограничениях
где Определение: Симметричной формой записи задачи линейного программирования называют задачу:
при ограничениях
или задачу при ограничениях
Определение: Канонической формой записи задачи линейного программирования называют задачу:
при ограничениях
Рассмотрим еще два вида записи- матричную и векторную. Введем обозначения:
где С – матрица-строка; А – матрица системы уравнений, Х – матрица-столбец переменных, Каноническая форма записи примет вид:
или max Z=CX при ограничениях
или
Запишем задачу линейного программирования в векторной форме:
Тогда задача линейного программирования в канонической форме записи имеет вид:
при ограничениях
где
1.10. Способы преобразования
При необходимости задачу минимизации можно заменить задачей максимизации и наоборот. Для функции одной переменной это утверждение очевидно. В самом деле, если Итак, min f(
Рис. 1. Графики функций y=f(x) и y=-f(x). То же самое имеет место в случае функции n переменных:
Случай 2. Пусть система ограничений ЗЛП представлена в виде:
Приведем систему к каноническому виду. Для этого прибавим к левым частям неравенств новые неотрицательные переменные.
Переменные Случай 3. Пусть система ограничений ЗЛП представлена в виде:
Система представлена в каноническом виде. однако, в отличие от случая 1, среди уравнений системы нет таких, которые представлены в предпочтительном виде. В этом случае говорят, что есть необходимость решать М-задачу. Для того, чтобы построить М-задачу необходимо прибавить к каждому уравнению системы ограничений дополнительные переменные. Будем их обозначать
при
Переменные Теорема 1: Если в оптимальном плане Теорема 2: Если в оптимальном плане М-задачи хотя бы одна из искусственных переменных не равна 0, то исходная задача не имеет допустимых планов, т.е. ее условия несовместны.
Случай 4. Пусть система ограничений ЗЛП представлена в виде:
Приведем систему к каноническому виду. Для этого вычтем из левых частей неравенств новые неотрицательные переменные.
Переменные Рассмотрены всевозможные варианты составления начального опорного плана. Однако, следует отметить, что на практике чаще всего встречаются смешанные системы ограничений, т.е. системы где есть уравнения, содержащие предпочтительную переменную, не содержащие таковую, неравенства. Для каждого ограничения такой системы находится своя предпочтительная переменная. Пример 3: Составить начальный опорный план при решении ЗЛП:
при
Решение. Первое уравнение системы имеет предпочтительный вид (случай 1). Предпочтительная переменная
В целевую функцию новая переменная войдет с коэффициентом, равным –М. Третье ограничение имеет вид неравенства ≤ (случай 2). Необходимо добавить дополнительную переменную Таким образом, ЗЛП будет иметь следующий вид:
при
Базис системы составляют переменные: Замечание: При составлении начального опорного плана для данной задачи учитывались все новые переменные в следующей последовательности: сначала переменные
2.6. Признак оптимальности опорного плана. Симплексные таблицы
Для того, чтобы было удобнее решать ЗЛП симплексным методом были придуманы симплексные таблицы, которые позволяют максимально алгоритмизировать процесс решения задачи линейного программирования. Симплексная таблица составляется только в том случае, если составлен начальный опорный план. Пусть ЗЛП представлена в каноническом виде:
при С помощью метода Гаусса (см. 1.12) преобразуем систему ограничений и приведем ее к следующему виду:
при
| |||||||||||||||||||||||||
|
| Поделиться: |













 Кроме элементов решения в любой задачи исследования операций имеются еще и заданные условия, которые фиксированы в условии задачи и нарушены быть не могут. В частности, к таким условиям относятся средства (материальные, технические, людские), которыми можно распоряжаться, и иные ограничения, налагаемые на решение. В своей совокупности они образуют так называемое «множество возможных решений». Обозначим это множество Х, а тот факт, что решение х принадлежит этому множеству, будем записывать: хÎХ.
Кроме элементов решения в любой задачи исследования операций имеются еще и заданные условия, которые фиксированы в условии задачи и нарушены быть не могут. В частности, к таким условиям относятся средства (материальные, технические, людские), которыми можно распоряжаться, и иные ограничения, налагаемые на решение. В своей совокупности они образуют так называемое «множество возможных решений». Обозначим это множество Х, а тот факт, что решение х принадлежит этому множеству, будем записывать: хÎХ. Задача 2. О смесях.
Задача 2. О смесях. . Предприятие при производстве этих видов продукции должно ограничиваться имеющими видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т.д.). Пусть их число равно m, припишем им индекс i
. Предприятие при производстве этих видов продукции должно ограничиваться имеющими видами ресурсов, технологий, других производственных факторов (сырья, полуфабрикатов, рабочей силы, оборудования, электроэнергии и т.д.). Пусть их число равно m, припишем им индекс i  . Они ограничены, и их количества равны соответственно
. Они ограничены, и их количества равны соответственно  условных единиц. Таким образом,
условных единиц. Таким образом,  - вектор ресурсов. Известна экономическая выгода (мера полезности) производства продукции каждого вида, исчислимая, скажем, по отпускной цене товара, его прибыльности, издержкам производства, степени удовлетворения потребностей и т.д.
- вектор ресурсов. Известна экономическая выгода (мера полезности) производства продукции каждого вида, исчислимая, скажем, по отпускной цене товара, его прибыльности, издержкам производства, степени удовлетворения потребностей и т.д. Примем в качестве такой меры, например, цену реализации
Примем в качестве такой меры, например, цену реализации  (
( ), т.е.
), т.е.  - вектор цен. Известны также технологические коэффициенты
- вектор цен. Известны также технологические коэффициенты  , которые указывают, сколько единиц i-го ресурса требуется для производства единицы продукции j-го вида. Матрицу коэффициентов ||
, которые указывают, сколько единиц i-го ресурса требуется для производства единицы продукции j-го вида. Матрицу коэффициентов ||  .
. - план производства, показывающий какие виды товаров нужно производить и в каких количествах, чтобы обеспечить предприятию максимум объема реализации при имеющихся ресурсах.
- план производства, показывающий какие виды товаров нужно производить и в каких количествах, чтобы обеспечить предприятию максимум объема реализации при имеющихся ресурсах.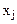 единиц будет равна
единиц будет равна  , а общий объем реализации:
, а общий объем реализации: .
. - расход i-го ресурса на производство
- расход i-го ресурса на производство  (
( ) единиц:
) единиц:
 , (
, ( ,
, (
( ),
), ,
, (
( (
( (
( .
. - затраты на перевозку единицы продукта из i-го пункта производства в j-тый пункт потребления. Обозначим через
- затраты на перевозку единицы продукта из i-го пункта производства в j-тый пункт потребления. Обозначим через  количество продукта, перевозимое из i-го пункта производства в j-тый пункт потребления. Матрица С=||
количество продукта, перевозимое из i-го пункта производства в j-тый пункт потребления. Матрица С=|| 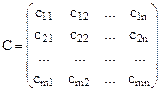

























 ,
, (
( (
(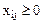 (
(
 1.9. Основные виды записи задач линейного программирования
1.9. Основные виды записи задач линейного программирования
 );
); (
( );
); (
( );
);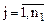 );
); ),
),
 ,
, ,
,  ,
, - матрица-столбец свободных членов.
- матрица-столбец свободных членов.
 ,
, 
 ,
,  ,
,  ,...,
,...,  ,...,
,...,  .
.
 ,
, 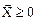 ,
, - скалярное произведение векторов
- скалярное произведение векторов  .
. - точка максимума функции y=f(x), то для функции y=-f(x) она является точкой максимума, так как графики функций f(x) и –f(x) симметричны относительно оси абсцисс (рис. 1).
- точка максимума функции y=f(x), то для функции y=-f(x) она является точкой максимума, так как графики функций f(x) и –f(x) симметричны относительно оси абсцисс (рис. 1).
 .
. (
(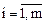 ),
),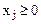 (
(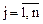 )
) (
(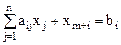 (
( )
) (
(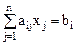 (
( .
.  будем называть искусственным базисом. Все переменные искусственного базиса – неотрицательны. В целевую функцию они входят с коэффициентом М (бесконечно большое положительное число). Знак коэффициента определяется в зависимости от того, какая ЗЛП решается. Если ЗЛП на максимум, то коэффициент (–М). В противном случае – (+М). Таким образом ЗЛП имеет вид:
будем называть искусственным базисом. Все переменные искусственного базиса – неотрицательны. В целевую функцию они входят с коэффициентом М (бесконечно большое положительное число). Знак коэффициента определяется в зависимости от того, какая ЗЛП решается. Если ЗЛП на максимум, то коэффициент (–М). В противном случае – (+М). Таким образом ЗЛП имеет вид: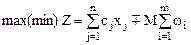
 (
( (
( М-задачи все искусственные переменные
М-задачи все искусственные переменные  является оптимальным для исходной задачи.
является оптимальным для исходной задачи. (
( (
(


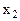 . Второе уравнение не содержит предпочтительной переменной (случай 2). Необходимо добавить одну переменную искусственного базиса
. Второе уравнение не содержит предпочтительной переменной (случай 2). Необходимо добавить одну переменную искусственного базиса  . Получим уравнение:
. Получим уравнение: .
. . Она и будет иметь предпочтительный вид. В целевую функцию она войдет с коэффициентом 0.). Следовательно, вычтем из левой части неравенства
. Она и будет иметь предпочтительный вид. В целевую функцию она войдет с коэффициентом 0.). Следовательно, вычтем из левой части неравенства 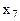 и добавим вторую переменную искусственного базиса
и добавим вторую переменную искусственного базиса  . Соответственно, в целевую функцию добавятся две новые переменные с коэффициентами 0 и –М соответственно.
. Соответственно, в целевую функцию добавятся две новые переменные с коэффициентами 0 и –М соответственно.




 (i=
(i= 


