Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение задач линейного программирования графическим методомСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Решение задачи линейного программирования графическим методом производится по следующему алгоритму: 1. Интерпретируется система ограничений. Строится область допустимых решений. 2. Строится произвольная линия уровня. Замечание: При решении ЗЛП графическим методом удобнее всего строить линию уровня при Z=0. 3. Выбирается направление перемещения линии уровня. Замечание1: Направление перемещения линии уровня выбирается с учетом направления наибольшего изменения функции. Это направление определяется с помощью градиента: grad Z = Если решается задача на max, то выбирается направление вектора градиента (направление вектора Замечание 2: С помощью вектора 4. Перемещается линия уровня, до тех пор, пока не найдено решение ЗЛП. Замечание 1: При решении ЗЛП возможны следующие случаи:
Рис. 8 Рис. 9.
Рис. 10 Рис. 11 На рис. 8 показан случай, когда минимум и максимум целевой функции найдены и находятся соответственно в точках max и min. Во втором случае (рис. 9) минимум целевой функции существует. Однако область допустимых решений не ограничена сверху, следовательно, максимума у целевой функции нет. В третьем случае (рис. 10) нет ни минимума, ни максимума функции. На рис.11 ЗЛП имеет бесконечно много решений. Пример1: Решить ЗЛП графическим методом. Найти:
при
Решение. Найдем градиент: Построим область допустимых значений. Для этого построим прямые, соответственные ограничениям:
Решение находится, исходя из решения системы:
Тогда: Ответ: Z= – Пример 2. Решить ЗЛП графическим методом. Найти:
при
Решение. Задачи, представленные в канонической форме можно решать графическим методом только в том случае, если разность между порядком и рангом системы ограничений равна 2. В данном случае: 5-3=2. Представим задачу таким образом, чтобы можно было решать графическим методом. Для этого в системе ограничений выразим переменные
Так как все переменные неотрицательны, то можно составить систему неравенств:
Подставим в целевую функцию вместо
Таким образом, ЗЛП имеет вид:
при
Найдем градиент: Построим область допустимых значений. Для этого построим прямые, соответственные ограничениям:
Область допустимых решений не ограничена сверху. Значит, решений нет. Ответ: Решений нет.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-07; просмотров: 536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.164.100 (0.007 с.) |

 =(
=(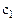 ,
,  )
)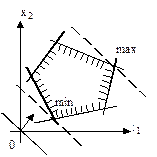
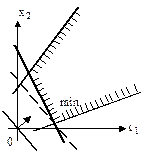



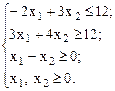
 (2;-3).
(2;-3).
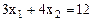



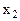




 2
2










 =
=  ;
;  =
=  .
.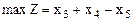

 ,
, 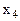 и
и  через
через