
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 3. Решение злп со многими переменными графическим методомСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оглавление
§ 1. Область применения графического метода решения ЗЛП Решение ЗЛП графическим методом в трехмерном пространстве ЗЛП со многими переменными, сводимые к задаче с двумя переменными
§ 2. Алгоритм решения ЗЛП со многими переменными графическим методом Описание алгоритма Пример
§ 1. Область применения графического метода решения ЗЛП
Графический метод основан на геометрической интерпретации задачи линейного программирования и применяется в основном при решении задач двумерного пространства (т.е. на плоскости). Графический метод можно использовать и при решении ЗЛП в трехмерном пространстве. Пусть, например задача линейного программирования имеет вид: F=c 1 x 1 +c 2 x 2 +c 3 x 3 при ограничениях
a 21 x 1 +a 22 x 2 +a 23 x 3 и при условии x 1 В пространстве любое линейное уравнение задает некоторую плоскость, а линейное неравенство – часть пространства с какой-либо стороны от граничной плоскости. Таким образом, множество допустимых решений ЗЛП в трехмерном пространстве образует пространственный многогранник R (Рис.1). Линии уровня целевой функции также являются плоскостями, которые пересекают многогранник R.

Рис.1. Перемещая нулевую линию уровня параллельно себе по направлению вектора-градиента с координатами (c 1, c 2, c 3) до последней точки многогранника решений, мы находим оптимальное решение. Однако графическое представление ЗЛП уже в трехмерном пространстве затруднительно, а в пространствах размерности больше трех изобразить графически ЗЛП вообще невозможно. Таким образом, применять графический метод целесообразно лишь в ЗЛП, имеющих две переменные.
На практике большинство задач линейного программирования имеют более двух переменных, и, казалось бы, решать их графическим методом нельзя. Это не совсем так. В линейном программировании существует множество задач, которые могут быть сведены к задаче с двумя переменными, следовательно, их можно решать графически. Для того, чтобы задачу линейного программирования со многими переменными можно было бы свести к задаче с двумя переменными, необходимо, чтобы ее система ограничений содержала не только неравенства, но и уравнения. При этом, число линейно независимых уравнений l должно быть на 2 меньше, чем число неизвестных n, т.е. n – l = 2. Если ЗЛП записана в каноническом виде (т.е. ее система ограничений состоит только из уравнений), то ее можно решить графическим методом при том же условии: если число неизвестных n и число линейно независимых уравнений m связаны соотношением: n – m = 2. Как определить число линейно независимых уравнений? Их коэффициенты не должны быть пропорциональны. Например, уравнения
линейно зависимы. Все коэффициенты второго уравнения равны соответственно коэффициентам первого уравнения, умноженным на 2. Таким образом, если в системе ограничений ЗЛП число линейно независимых уравнений на 2 меньше, чем число неизвестных, то ее можно решить графически. §2. Алгоритм решения ЗЛП со многими переменными графическим методом
Допустим, что задачу линейного программирования со многими переменными можно свести к задаче с двумя переменными, т.е в ее системе ограничений число линейно независимых уравнений на 2 меньше, чем число неизвестных. Тогда, придерживаемся следующей схемы действий: 1) преобразовывая эти линейно независимые уравнения, выражаем п –2 переменные через какие-то две, например х 1 и х 2; 2) полученные выражения подставляем во все остальные ограничения системы, в условия неотрицательности и в целевую функцию – получаем ЗЛП с двумя переменными (х 1 и х 2); 3) решаем задачу графическим методом и находим оптимальный план Х = (х 1*, х 2*); 4) подставляем найденные значения оптимального плана х 1* и х 2* в выражения для остальных переменных и получаем окончательное решение. Рассмотрим применение этого алгоритма на примере.
Пример. Двум погрузчикам разной мощности за 24 часа нужно погрузить на первой площадке 230 т., на второй 168 т. Первый погрузчик на первой площадке может погрузить 10 т. в час, на второй – 12 т. Второй – на каждой площадке может погрузить по 13 т. в час. Стоимость работ, связанных с погрузкой 1 т. первым погрузчиком на первой площадке составляет 8 р., на второй площадке – 7 р. Стоимость погрузки вторым погрузчиком на первой площадке составляет 12 р., на второй – 13 р. Нужно составить такой план работы (т.е. найти, какой объем работ должен выполнить каждый погрузчик на каждой площадке), чтобы стоимость всех работ по погрузке была минимальной, учитывая, что по техническим причинам первый погрузчик на второй площадке должен работать не более 16 часов. Решение. Для начала составим математическую модель данной задачи. Обозначим: х 1 – объем работ (в тоннах) 1-го погрузчика на первой площадке; х 2 – объем работ (в тоннах) 1-го погрузчика на второй площадке; х 3 – объем работ (в тоннах) 2-го погрузчика на первой площадке; х 4 – объем работ (в тоннах) 2-го погрузчика на второй площадке. Тогда, из условия, что «первый погрузчик на первой площадке может погрузить 10 т. в час, на второй – 12 т. в час» время его работы на первой площадке равно Часть условий задачи перенесем в таблицу (Таблица 1). Таблица 1.
По условию, погрузчики работают 24 часа, т.е. для каждого погрузчика сумма времени его работы на обеих площадках не превосходит 24 часов, тогда можно записать ограничения:
Из условия, что «первый погрузчик на второй площадке должен работать не более 16 часов», получим следующее ограничение:
Кроме того, по условию «нужно погрузить на первой площадке 230 т., на второй 168 т.», следовательно:
Целевую функцию запишем на основании условия задачи, что «стоимость работ, связанных с погрузкой 1 т. первым погрузчиком на первой площадке составляет 8 р., на второй площадке – 7 р. Стоимость погрузки вторым погрузчиком на первой площадке составляет 12 р., на второй – 13 р.»:
К этому необходимо добавить условие неотрицательности:
Итак, математическая модель задачи имеет вид:
при ограничениях:
В системе ограничений есть l = 2 линейно независимых уравнения и n = 4 переменных, тогда n – l = 4 – 2 = 2, следовательно, эту задачу можно решить графическим методом. 1. Из уравнения Из уравнения 2. Подставим эти выражения в систему ограничений:
в условие неотрицательности:
в целевую функцию:
После арифметических преобразований, исключения избыточных условий и замены целевой функции Z = – F получим ЗЛП с двумя переменными:
3. Графическое решение задачи представлено на рисунке (Рис.2). Оптимальный план – точка пересечения 1-ой и 4-ой прямых, т.е.
откуда Х опт. = (100, 168), Z max = – 3536. 4. Для определения остальных переменных, подставим значения
Таким образом, оптимальный план задачи равен Х опт. = (100, 168, 130, 0). Для определения значения F min воспользуемся свойством min F = – max (– F). В нашем случае – F = Z, следовательно F min= – Zmax = – (–3536) = 3536.
Рис.2.
Итак, по оптимальному плану первый погрузчик должен погрузить 100 т. на первой площадке и 168 т. на второй, второму погрузчику надлежит погрузить 130 т. на первой площадке. Стоимость всех работ составит 3536 р.
В заключении отметим, что графический метод решения ЗЛП представляет большой интерес с точки зрения выработки наглядных представлений о сущности задач линейного программирования. Задачу линейного программирования с двумя переменными всегда можно решить графически. Однако уже в трехмерном пространстве такое решение усложняется, а в пространствах размерностью больше трех графическое решение возможно только для отдельного ряда задач. Таким образом, данный метод решения задачи линейного программирования имеет очень узкие рамки применения.
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 4254; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

 max
max a 11 x 1 +a 12 x 2 +a 13 x 3
a 11 x 1 +a 12 x 2 +a 13 x 3  b 1
b 1 0, x 2
0, x 2  и
и 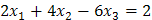
 часов, на второй площадке – равно
часов, на второй площадке – равно 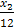 часов; из условия, что «второй погрузчик на каждой площадке может погрузить по 13 т. в час» время работы второго погрузчика на первой площадке равно
часов; из условия, что «второй погрузчик на каждой площадке может погрузить по 13 т. в час» время работы второго погрузчика на первой площадке равно  часов, на второй площадке – равно
часов, на второй площадке – равно  часов.
часов.










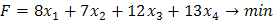











 ,
, и
и  в уравнения:
в уравнения: 
 .
.



