
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы решения транспортной задачиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Транспортную задачу можно решить и симплекс-методом, но в данном случае этот метод неэффективен, так как используются ограничения специального вида. Поэтому обычно решают задачи транспортного типа с помощью алгоритма последовательного улучшения плана. Алгоритм последовательного улучшения плана предусматривает два этапа решения задачи: · определение исходного опорного решения; · последовательное улучшение опорного решения и приближение к оптимальному плану. Для определения опорного решения обычно используют метод северо-западного угла. В этом случае исходные данные записываются несколько в ином виде (таблица 3).
Таблица 3. Поиск опорного решения
Заполнение таблицы начинаем с клетки (1,1), которая находится в северо-западном углу таблицы, отсюда и название метода.
Получили опорное решение. Этому решению соответствуют затраты:
Опорное решение является допустимым, так как значения управляемых переменных неотрицательны и выполнены ограничения на объемы производства и потребления. Опорный план транспортной задачи должен содержать не больше чем В рассматриваемом примере Кроме того, опорный план должен быть ацикличным, т.е. в таблице нельзя построить замкнутый цикл, все вершины которого лежат в занятых клетках, а стороны расположены под прямым углом друг к другу. Поэтому нулевые поставки для избавления от вырожденности плана нельзя вводить в клетки таблицы, образующие цикл балансового перерасчета. Так как в таблице 3 нет замкнутых циклов, то опорное решение ацикличное. Так как при выборе опорного решения не обращали внимание на стоимости перевозок, то полученный план закрепления потребителей за поставщиками скорее всего неоптимальный и его можно улучшить. Поставим задачу: как можно больше перевозить с минимальной стоимостью. Эта идея заложена в методе минимальной стоимости. В этом случае на каждом шаге заполняют клетку таблицы с наименьшей стоимостью доставки единицы продукции. При этом необходимо учитывать это обстоятельство для всех поставщиков. Расчет выполнен в таблицах 4-6. Начинаем заполнение таблицы 4 с клетки (1,4), затем переходим к клетке (1,1), потом к клетке (2,1) и т.д., при этом каждый раз фиксируем остатки на заводах и объектах. В итоге такого распределения получим транспортные расходы:
Таблица 4. Вариант 1 улучшенного плана
Таблица 5. Вариант 2 улучшенного плана
Таблица 6. Вариант 3 улучшенного плана
Планы, полученные в таблицах 4-6 допустимы, невырождены и ацикличны. Как видим, расходы уменьшаются, но нет уверенности в том, что полученные планы оптимальны. При большой размерности задачи поиск плана методом минимальной стоимости усложняется. В этом случае используют другие методы поиска опорного плана (метод двойного перевеса, метод аппроксимации Фогеля).
Метод потенциалов В теории линейного программирования доказывается, что любая транспортная задача имеет оптимальный план. Возникает вопрос: как проверить план на оптимальность и будет ли единственным оптимальный план? Существует простая методика проверки планов на оптимальность. В основу ее положен метод потенциалов. Смысл его заключается в следующем. Каждому заводу поставщику присваивают некоторую величину · для переменных · для переменных Здесь Алгоритм метода потенциалов 1. Устанавливают вид модели транспортной задачи (открытая или закрытая). При необходимости делают модель закрытой. 2. Определяют первый опорный план с учетом стоимости доставки продукции. 3. Проверяют опорный план на вырожденность. При необходимости вводят нулевые поставки. 4. Проверяют опорный план на оптимальность. Для чего определяют потенциалы поставщиков и потребителей по выражениям (5) для базисных переменных и анализируются неравенства (6) для свободных переменных: · если хотя бы одно из неравенств не выполняется, то план неоптимальный и для его улучшения изменяют значение свободной переменной невыполняемого неравенства; · если все неравенства выполняются и среди неравенств имеются равенства, то план оптимальный и не единственный. Проверим алгоритм метода на примере 1. Исходная модель транспортной задачи является закрытой. В качестве первого опорного плана возьмем вариант 2 (таблица 5). Вариант 2. Базисные переменные (заполненные клетки):
Количество заполненных клеток на единицу меньше суммы количества поставщиков и потребителей, т.е. опорный план невырожденный. Для нахождения значений потенциалов составляем систему равенств:
Так как равенств 6, а неизвестных 7, то система является неопределенной. Поэтому для определенности системы считаем значение одного из потенциалов известным, например,
Составляем неравенства для незаполненных клеток и анализируем их
Одно из неравенств не выполняется, следовательно, план неоптимальный. Это неравенство соответствует переменной
Так как суммы значений неизвестных по строкам и столбцам должны оставаться неизменными, то следует произвести балансовый перерасчет (см. таблицу 5). В итоге перерасчета приходим к варианту 1 (см. таблицу 4). Выполним анализ варианта 3 (таблица 6). Вариант 3. Базисные переменные:
Опорный план невырожденный. Составляем систему равенств, определяемых базисными переменными:
Так как равенств 6, а неизвестных 7, то полагаем
Составляем неравенства для незаполненных клеток
Все неравенства выполняются и среди неравенств имеются равенства, следовательно, план оптимальный и не единственный. Равенства соответствуют переменным
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 558; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.227.3 (0.011 с.) |


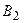






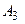
 и первый столбец закрыт, потребности строительного объекта
и первый столбец закрыт, потребности строительного объекта  , закрыта первая строка, исчерпаны мощности завода
, закрыта первая строка, исчерпаны мощности завода  , закрыт 2-й столбец, потребности строительного объекта
, закрыт 2-й столбец, потребности строительного объекта  , закрыта вторая строка, мощности завода
, закрыта вторая строка, мощности завода 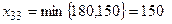 , закрыт 3-й столбец, потребности строительного объекта
, закрыт 3-й столбец, потребности строительного объекта  , закрыты все строки и столбцы.
, закрыты все строки и столбцы.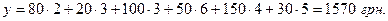
 отличных от нуля компонент (заполненных клеток таблицы). Если их количество равно
отличных от нуля компонент (заполненных клеток таблицы). Если их количество равно 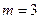 и
и  Опорный план (таблица 3) имеет 6 заполненных клеток, т.е. выполняется условие
Опорный план (таблица 3) имеет 6 заполненных клеток, т.е. выполняется условие  и опорный план невырожденный.
и опорный план невырожденный.
 =50
=50



 которую называют потенциалом завода, а каждому строительному объекту – величину
которую называют потенциалом завода, а каждому строительному объекту – величину  - потенциал строительного объекта. Эти величины связаны между собой соотношениями:
- потенциал строительного объекта. Эти величины связаны между собой соотношениями: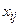 заполненных клеток (базисных переменных)
заполненных клеток (базисных переменных)  (5)
(5) незаполненных клеток (свободных переменных)
незаполненных клеток (свободных переменных)  (6)
(6)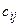 - стоимость доставки единицы продукции от
- стоимость доставки единицы продукции от  -го завода к
-го завода к 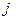 - му строительному объекту заполненных клеток,
- му строительному объекту заполненных клеток,  - стоимость доставки для незаполненных клеток.
- стоимость доставки для незаполненных клеток.

 , тогда:
, тогда:

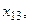 т.е. для улучшения плана необходимо эту переменную ввести в басис, присвоив ей некоторую величину
т.е. для улучшения плана необходимо эту переменную ввести в басис, присвоив ей некоторую величину 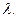 Переход к новому базису осуществляется с помощью построения цикла и перераспределения перевозимой продукции. Строим цикл с вершинами в занятых клетках (1,1), (2,1), (2,3) и незанятой клетки (1,3), в которой не выполняются условия оптимальности. Для определения величины
Переход к новому базису осуществляется с помощью построения цикла и перераспределения перевозимой продукции. Строим цикл с вершинами в занятых клетках (1,1), (2,1), (2,3) и незанятой клетки (1,3), в которой не выполняются условия оптимальности. Для определения величины 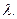 в незанятую клетку (1,3) поставим знак «+», а другие вершины цикла отметим чередованием знаков «-» и «+» (см. таблицу 5). Затем определяем
в незанятую клетку (1,3) поставим знак «+», а другие вершины цикла отметим чередованием знаков «-» и «+» (см. таблицу 5). Затем определяем  где
где  - количество продукции в клетках вершин цикла, отмеченных знаком «-»:
- количество продукции в клетках вершин цикла, отмеченных знаком «-»:


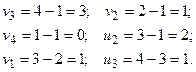

 Изменяя значения этих переменных, можно получить новые оптимальные планы. Один из них приведен в таблице 4.
Изменяя значения этих переменных, можно получить новые оптимальные планы. Один из них приведен в таблице 4.


