
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Признак единственности решения злп, найденного симплекс методом.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Если оценки всех свободных векторов-столбцов 4) Если оптимальное решение не найдено, ищем новое опорное решение.
Признак отсутствия оптимального решения в силу неограниченности целевой функции. ЗЛП не имеет решения в силу неограниченности целевой функции, если какой-нибудь столбец коэффициентов свободной переменной, оценка которого противоречит признаку оптимальности, не содержит ни одного положительного элемента.
Если условие отсутствия оптимального решения не выполняется, введём в базис новую переменную, столбец коэффициентов которой имеет оценку, противоречащую признаку оптимальности. Если таких столбцов несколько, выбираем столбец с «наихудшей» оценкой. Для выбора разрешающего элемента в столбце новой базисной переменной используем условие неотрицательности свободных членов. Из базиса выводится столбец с разрешающим элементом (единицей) в соответствующей строке. Получив новое опорное решение, вычисляем соответствующее ему значение целевой функции. заполняем первые два столбца симплекс таблицы, вычисляем оценки векторов столбцов коэффициентов при свободных переменных (см. выше), проверяем выполнение признаков оптимальности и единственности найденного решения: если все оценки столбцов свободных переменных положительны, найден максимум ЗЛП, если все оценки столбцов свободных переменных отрицательны, найден минимум ЗЛП, если хотя бы одна из оценок столбцов свободных переменных равна нулю, решений бесконечно много, они находятся по формуле
Приращение целевой функции при переходе от одного опорного решения к другому можно вычислить по формуле:
16. Основы теории двойственности. Правила построения задачи, двойственной к данной. 1.) Если целевая функция одной задачи в паре стремится к минимуму, то целевая функция другой задачи стремится к максимуму. 2) Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений в другой. 3) Количество переменных в двойственной задаче равно числу ограничений в исходной. 4)Матрицы коэффициентов при переменных в системах ограничений обеих задач являются транспонированными друг к другу. 5) Задача на максимум – все ограничения с 6) Если в системе ограничений задачи k-е ограничение является равенством, то на k-ю переменную в двойственной задаче не накладывается условие неотрицательности.
Первая теорема двойственности: Если одна из пары двойственных задач имеет оптимальное решение, то и двойственная к ней имеет оптимальное решение. Причём значения целевых функций этих задач на своих оптимальных решениях совпадают. Оптимальное решение одной из задач можно найти из решения симплекс методом другой задачи, прибавив к оценкам разложений по базису оптимального решения векторов, входящих в начальный базис начального решения соответствующие коэффициенты целевой функции. Если одна из пары двойственных задач не имеет решения ввиду неограниченности целевой функции, то другая не имеет решения ввиду несовместности системы ограничений. Вторая теорема двойственности: Допустимые решения
17. Постановка транспортной задачи. Транспортные задачи – целочисленные задачи линейного программирования в канонической форме, коэффициенты при переменных в ограничениях равны нулю или единице и каждая переменная входит в систему ограничений два раза. Эти задачи можно решать обычным симплекс-методом, но мы рассмотрим более удобные специальные методы решения транспортных задач. Дано: Несколько (m) поставщиков однородного товара хотят передать этот товар нескольким (n) потребителям. Мощность i го поставщика
Задача: Для каждой пары «поставщик-потребитель» определить объём перевозки
Полученная матрица перевозок должна удовлетворять следующим условиям: 1) суммарные затраты на перевозку минимальны;
(Сумма затрат на перевозку 2) мощности всех поставщиков реализованы; 3) запросы всех потребителей удовлетворены
В транспортной задаче n+m уравнений ограничений, n.m переменных; из них n+m+1 линейно независимых уравнений и 18. Постановка транспортной задачи. Методы поиска начальных решений.
Несколько (m) поставщиков однородного товара хотят передать этот товар нескольким (n) потребителям. Мощность i го поставщика В клетку (i,j) таблицы поставок вносим максимально возможный объём перевозки, равный оставшимся запасам i-го поставщика или неудовлетворённым потребностям j -го потребителя. Затем вычёркиваем из таблицы поставщика или потребителя, потребности которого полностью удовлетворены. (одна заполненная клетка таблицы – один вычеркнутый ряд матрицы). Метод северо-западного угла: последовательнозаполняем правую верхнюю клетку таблицы поставок. Метод минимальной стоимости – в первую очередь заполняем клетки с наименьшей стоимостью первозки. В транспортной задаче n+m уравнений ограничений, n.m переменных; из них n+m+1 линейно независимых уравнений и Необходимое и достаточное условие существования решения транспортной задачи. Суммарные запасы (мощности) поставщиков и потребителей равны между собой (задача закрыта, или задача с правильным балансом).
Построение начального решения: В клетку (i,j) таблицы поставок вносим максимально возможный объём перевозки, равный оставшимся запасам i-го поставщика или неудовлетворённым потребностям j -го потребителя. Затем вычёркиваем из таблицы поставщика или потребителя, потребности которого полностью удовлетворены. (одна заполненная клетка таблицы – один вычеркнутый ряд матрицы). Метод северо-западного угла: последовательнозаполняем правую верхнюю клетку таблицы поставок. Метод минимальной стоимости – в первую очередь заполняем клетки с наименьшей стоимостью первозки. 19. Понятие сдвига по циклу в транспортной задаче. Методы поиска оптимального решения. Критерии оптимальности найденного решения.
Цикл клетки (i,j) – последовательность клеток таблицы ТЗ, определяемая ломаной линией, состоящей из вертикальных и горизонтальных звеньев. Начало и конец ломаной – в клетке (i,j), остальные вершины – в заполненных клетках таблицы. Допустимое решение ТЗ является базисным тогда и только тогда, когда из заполненных им клеток таблицы нельзя образовать ни одного цикла. Алгоритм решения ТЗ, 1) находим начальное базисное допустимое (опорное) решение, состоящее из (n+m+1) заполненных клеток таблицы поставок методом северо-западного угла или методом минимальной стоимости. Убеждаемся в его «опорности» методом вычёркивания рядов с одной заполненной клеткой из матрицы поставок. 2) проверяем оптимальность найденного решения (используя различные критерии оптимальности) 3) если найденное решение не оптимально, изменяем его, используя «сдвиг по циклу»: увеличиваем объём перевозок во всех нечётных клетках цикла и уменьшаем во всех чётных на величину
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 528; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.011 с.) |

 не равны нулю, найденное оптимальное решение единственно.
не равны нулю, найденное оптимальное решение единственно. , где
, где  находим путём перебора всех опорных решений ЗЛП].
находим путём перебора всех опорных решений ЗЛП].
 . В задаче на минимум – все ограничения с
. В задаче на минимум – все ограничения с 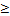 .
. и
и 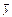 являются оптимальными решениями пары двойственных задач тогда и только тогда, когда
являются оптимальными решениями пары двойственных задач тогда и только тогда, когда 
 и
и 

 - равна запасам товара у этого поставщика. Мощности поставщиков заносятся в первый столбец таблицы поставок. Мощность j -го потребителя -
- равна запасам товара у этого поставщика. Мощности поставщиков заносятся в первый столбец таблицы поставок. Мощность j -го потребителя -  - определяется количеством необходимого ему товара. Мощности потребителей равны их запросам. Известна стоимость перевозки единицы товара от каждого из поставщиков к каждому потребителю -
- определяется количеством необходимого ему товара. Мощности потребителей равны их запросам. Известна стоимость перевозки единицы товара от каждого из поставщиков к каждому потребителю -  .
.





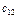



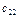






 , то есть составить оптимальныйплан перевозок товара.
, то есть составить оптимальныйплан перевозок товара.



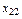


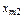



 равна сумме произведений объёмов перевозок товара
равна сумме произведений объёмов перевозок товара 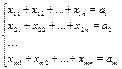

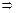 n+m+1 базисных переменных (заполненных клеток в таблице поставок). Число свободных клеток n.m – (n+m+1) равно числу свободных переменных задачи.
n+m+1 базисных переменных (заполненных клеток в таблице поставок). Число свободных клеток n.m – (n+m+1) равно числу свободных переменных задачи. (
(


