
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Системный подход к задачам принятия решения.Содержание книги
Поиск на нашем сайте
Критерий минимизации размаха. - выбирается стратегия с минимальной разницей между откликами системы. (между наибольшей и наименьшей отдачей от стратегии.) R=xmax -xmin Критерий минимизации риска (среднекадратического отклонения, вычисленного в предположении о равновероятности состояний среды) Для вычисления дисперсии отдач при применении k- той стратегии, надо найти сумму квадратов элементов k- той строки платёжной матрицы делённую на их количество и, затем, вычесть из неё квадрат среднего арифметического исходов данной стратегии. Среднеквадратическое отклонение равно корню из дисперсии.
Критерий минимизации относительного риска - выбирается стратегия с наименьшим отношением риска (среднеквадратического отклонения) к ожидаемому среднему.
8. Основные понятия и общая постановка задачи теории игр. Геометрический метод поиска решения парной антагонистической игры. Основные понятия теории игр. Теория игр – математическая теория конфликтных ситуаций. Исследуются задачи о принятии решений в условиях неопределённости, обусловленной наличием мыслящего противника (или многих противников) Игра – математическая модель конфликтной ситуации. Игроки – стороны, участвующие в конфликте, а выигрыш – исход конфликта.
Общая постановка задачи теории игр. 1. Принимают решения n конфликтующих сторон – игроков, интересы которых не совпадают. 2. Определены правила выбора допустимых стратегий, известных игрокам. 3. Известен набор возможных конечных состояний игры (выигрыш, ничья, проигрыш и тд.) 4. Всем участникам игры заранее известны платежи, соответствующие каждому возможному конечному состоянию. Парная антагонистическая игра – игра, с нулевой суммой, в которую играют 2 игрока (игра, в которой выигрыш первого игрока равен проигрышу другого). Стратегия игрока - совокупность возможных действий игрока, определяющая результат игры. Чистая стратегия – действие игрока, определяющее результат игры.
Пусть игрок А располагает n личными чистыми стратегиями – А1, А2,….Аn, а игрок В имеет m личных стратегий B1, B2,….Bm. Тогда игра имеет размерность n ∙ m. Результаты игры задаём платёжной матрицей, в которой каждой i – той стратегии игрока А и j – той стратегии игрока В ставится в соответствии число аij., равное выигрышу игрока А и проигрышу игрока В. Теорема Неймана. Каждая конечная игра имеет хотя бы одно оптимальное решение, возможно, среди смешанных стратегий. Активная стратегия –чистая стратегия, входящая в оптимальную смешанную с ненулевой вероятностью. (невычеркнутые столбцы и строки) Теорема об активных стратегиях. Если один игрок придерживается своей оптимальной смешанной стратегии, то его выигрыш остаётся неизменным и равным цене игры V, если второй игрок не выходит за пределы своих активных стратегий. Находим начальное опорное решение. [составляем симплекс таблицу, преобразуем расширенную матрицу уравнений ограничений методом Жордано – Гаусса, разрешаем её относительно m базисных переменных, выбранных произвольно, но с соблюдением условия неотрицательности, приравниваем свободные переменные к нулю, вычисляем значения базисных переменных, находим значение целевой функции для найденного начального опорного решения]. 3) Проверяем найденное опорное решение на оптимальность. 15. Критерии оптимальности и единственности в симплекс методе. Правило вычисления оценок. Критерий отсутствия (существования) оптимального решения. Критерии оптимальности и единственности в симплекс методе. Правило вычисления оценок. Критерий отсутствия (существования) оптимального решения. Вычисление оценки разложения вектора условий
где
Алгоритм решения ТЗ, 1) находим начальное базисное допустимое (опорное) решение, состоящее из (n+m+1) заполненных клеток таблицы поставок методом северо-западного угла или методом минимальной стоимости. Убеждаемся в его «опорности» методом вычёркивания рядов с одной заполненной клеткой из матрицы поставок. 2) проверяем оптимальность найденного решения (используя различные критерии оптимальности) 3) если найденное решение не оптимально, изменяем его, используя «сдвиг по циклу»: увеличиваем объём перевозок во всех нечётных клетках цикла и уменьшаем во всех чётных на величину Системный подход к задачам принятия решения. Объект управления (управляемая подсистема) воздействует на субъект управления (управляющую подсистему) посредством альтернативных управляющих воздействий. На состояние объекта оказывают влияние управляющее воздействие + среда (среда не поддаётся воздействию, и полной информации о ней нет). Наилучшее решение –управляющее воздействие, наиболее соответствующее цели управляющей подсистемы в рамках имеющейся у неё информации о среде. Этапы исследования ЗПР: 1. построение математической модели ЗПР 2. Формулировка принципа оптимальности и нахождение оптимального решения. 3. анализ полученных результатов.
2. Типы и структуры задач принятия решения. Основные типы задач принятия решения (ПР): 1. ПР в условиях определённости. (состояние среды неизменно и управляющая система имеет о нём информацию) 2. ПР в условиях риска (известны все возможные состояния среды и распределение их вероятностей) 3. ПР в условиях неопределённости (известны только все возможные состояния среды) 4. ПР в условиях разумности среды (среда - другая управляющая подсистема, ситуация конфликта, игры).
Реализационная структура принятия решения – набор следующих объектов: - множество допустимых альтернатив управляющего воздействия {Si} - множество возможных состояний среды {Ni} - множество возможных исходов ((xij)) - функция реализации, определяющая соответствие между парами элементов (Si;Ni) и элементами исходов. Функция реализации задаётся платёжной матрицей. в которой строки соответствуют альтернативным стратегиям, а столбцы – множеству различных состояний среды. Элементы матрицы – исходы. Оценочная структура принятия решения - указывает оценку результата с точки зрения принимающего решения. Способы задания оценочной структуры: - оценочные функции, определяющие ценность исходов - разбиение исходов на классы предпочтений и т.д. 3. Постановка задачи принятия решения в условиях риска. Критерий максимизации ожидаемого отклика системы. Задача описывается матрицей решений (платёжной матрицей), в которой строки соответствуют альтернативным стратегиям ЛПР (лица, принимающего решение), а столбцы – множеству различных состояний среды. Элементы матрицы – исходы, или отдачи от применения различных стратегий соответствующих различным состояниям среды. Задачи принятия решений в условиях риска характеризуются наличием стохастической информации о состояниях среды (как правило, известны вероятности этих состояний). Будем считать отдачу от i-той стратегии дискретной случайной величиной, принимающей свои значения с вероятностями, равными вероятностям различных состояний среды. Тогда предполагаемая стоимость стратегии в условиях риска равна матожиданию исходов (отдач) стратегии, т.е. сумме произведений отдач на вероятности состояний среды, при которых они поступают. E(Si)= Критерий ожидаемого выигрыша: ЛПР принимает стратегию с самой высокой предполагаемой стоимостью E(Si). Если есть несколько стратегий с одинаковой предполагаемой стоимостью из них выбирают стратегию с наименьшим риском.
4. Способы оценки риска в ЗПР. Дана задача принятия решения в условях риска, т.е. заданы альтернативные стратегии, состояния среды и их вероятности Степень риска – показатель разброса отдач от стратегии относительно ожидаемого среднего значения. Грубый способ оценки риска - размах – разность между наибольшей и наименьшей отдачей от стратегии. R=xmax -xmin Более точная оценка риска – среднеквадратическое отклонение отдач от стратегии (чем выше риск, тем больше дисперсия). Относительный риск – отношение среднеквадратического отклонения к предполагаемой стоимости
Индекс риска – относительный риск, увеличенный в сто раз. 5. Постановка задачи принятия решения в условиях неопределённости. Критерий Гурвица принятия решения. Задача описывается матрицей решений (платёжной матрицей), в которой строки соответствуют альтернативным стратегиям ЛПР (лица, принимающего решение), а столбцы – множеству различных состояний среды. Элементы матрицы – исходы, или отдачи от применения различных стратегий соответствующих различным состояниям среды. Критерий оптимиста (максимакс) – выбирают стратегию, наилучший результат которой лучше наилучших результатов других стратегий. Критерий пессимиста (Вальда) (максимин) – выбирают стратегию, наихудший результат которой лучше наихудших результатов других стратегий. Критерий компромисса с заданным коэффициентом оптимизма (Гурвица) Для каждой стратегии определяют компромиссный результат как сумму наихудшего и наилучшего, взятых с коэффициентами α и (1-α). (α-коэффициент оптимизма). Выбирают стратегию с наилучшим компромиссным результатом. α J +(1-α) L = K 6. Как применяются критерии Сэвиджа, Лапласа и Гурвица в ЗПР в условиях неопределённости? Пусть Si – альтернативные воздействия на систему, m – число состояний среды, а Критерий недостаточного основания Лапласа (максимизация среднего отклика) – выбирается стратегия с наилучшим средним арифметическим откликов (результатов). E(Si) Критерий компромисса с заданным коэффициентом оптимизма (Гурвица) Для каждой стратегии определяют компромиссный результат как сумму наихудшего и наилучшего, взятых с коэффициентами α и (1-α). (α-коэффициент оптимизма). Выбирают стратегию с наилучшим компромиссным результатом. α J +(1-α) L = K Критерий минимизации недополученных прибылей (Сэвиджа) -составляется матрица недополученных прибылей, элементы которой равны разнице между максимальным элементов в столбце (наилучшим исходом при данном состоянии среды) и каждым элементом исходной матрицы. Данную матрицу анализируют по любому их вышеперечисленных критериев.
7. Критерии минимизации риска в условиях неопределённости.
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.011 с.) |

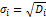 где
где 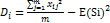
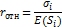
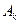 по базису опорного решения.
по базису опорного решения.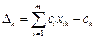 или
или 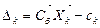 ,
, - вектор – столбец коэффициентов целевой функции при базисных переменных,
- вектор – столбец коэффициентов целевой функции при базисных переменных, 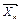 - вектор – столбец коэффициентов системы ограничений при k-ой переменной,
- вектор – столбец коэффициентов системы ограничений при k-ой переменной, 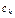 - коэффициент в целевой функции при k-ой переменной.
- коэффициент в целевой функции при k-ой переменной. (
(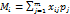
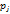 и платёжная матрица, элементы которой - исходы, или отдачи от применения различных стратегий соответствующих различным состояниям среды
и платёжная матрица, элементы которой - исходы, или отдачи от применения различных стратегий соответствующих различным состояниям среды 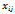 .
. 
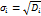 где
где 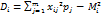
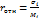
 отклики системы на управляющее воздействие. Тогда:
отклики системы на управляющее воздействие. Тогда: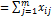 /m
/m


