
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраический метод поиска оптимальной смешанной стратегии.Содержание книги
Поиск на нашем сайте
Согласно теореме об активных стратегиях, если один игрок придерживается своей оптимальной смешанной стратегии, то его выигрыш остаётся неизменным и равным цене игры V, если второй игрок не выходит за пределы своих активных стратегий. После вычёркивания остаются только активные стратегии. Поэтому ожидаемый выигрыш от применения каждой стратегии постоянен и равен v. Для двух стратегий составляем два уравнения, неизвестными в которых будут вероятности применения стратегий противником и цена игры v. Дополнив систему уравнением «сумма вероятностей равна 1, получим систему из трёх линейных уравнений с тремя неизвестными. Решив её методом Крамера или Жордано –Гаусса, найдём искомую оптимальную смешанную стратегию и цену игры. Пусть Тогда
11. Постановка задачи математического программирования. Понятие допустимого и оптимального решения. Операция – управляемое мероприятие, направленное на достижение цели. Условие задачи математического программирования состоит из: (1) результата операций от её факторов, переменных ЗМП. (2)
… связи между факторами операции.,
Допустимым решением ЗМП называют любой n-мерный вектор Совокупность всех допустимых решений образуют область в n-мерном пространстве – ОДР. Решить ЗМП – выбрать из всех допустимых решений то, при котором результат операции будет наилучшим (целевая функция (1) достигнет своего наибольшего или наименьшего значения). Оптимальным решением ЗМП называется допустимое решение ЗМП, при котором целевая функция
12. Графический метод решения задач математического программирования. ( ЗМП). Рассмотрим ЗМП с двумя неизвестными:
1) Строим ОДР задачи. Областью решения каждого из неравенств Если ОДР – пустое множество, задача не имеет решения в силу несовместности системы ограничений. Если ОДР – непустое множество, задача может иметь одно или бесконечное множество решений. 2) Строим линии уровня целевой функции (линии, в которых значение функции постоянно).
Если Z – линейная функция, то её линии уровня – семейство прямых, перпендикулярных вектору градиенту этой функции. Вектором градиентом функции 3) Двигаясь от одной линии уровня к другой в направлении вектора градиента (в задачах на максимум) или в противоположном направлении (в задачах на минимум), находим опорную кривую. Опорная кривая _ такая линия уровня, которая имеет хотя бы одну общую точку с ОДР, и, при этом, не разделяет её на части.
4) Находим оптимальное решение задачи – общие точки ОДР и опорной кривой.
13. Симплекс метод решения ЗЛП. Определение и основания для применения. Структура симплекс таблицы. Симплекс метод – это метод целенаправленного перебора опорных решений задачи линейного программирования (ЗЛП). Основания для применения симплекс метода: 1) ОДР ЗЛП – выпуклое множество с конечным числом угловых точек; 2) оптимальное решение ЗЛП – это одна из угловых точек ОДР; 3) угловые точки ОДР – базисные решения (опорные планы) системы ограничений. Базисные решения – допустимые решения вида Все свободные переменные равны нулю, а базисные переменные равны соответствующим свободным членам в преобразованной (разрешённой относительно базисных переменных) системе ограничений.
14. Критерии оптимальности и единственности в симплекс методе. Правило вычисления оценок. Критерий отсутствия (существования) оптимального решения. Поиск начального базисного решения симплекс метода. Параметр соблюдения условия неотрицательности переменных.
Чтобы решения системы уравнений ограничений были допустимыми, должно выполняться условие неотрицательности свободных членов: При любых преобразованиях уравнений системы ограничений, свободные члены уравнений должны оставаться неотрицательными. Чтобы выполнить это условие, в процессе преобразований системы методом Жордано-Гаусса, выбираем разрешающий элемент в k-ом столбце только после вычисления вспомогательного параметра
[делим каждый свободный член на каждый элемент k-ого столбца, выбираем наименьшее отношение и по его местоположению определяем строку k-ого столбца, содержащую разрешающий элемент ]
Алгоритм применения симплекс – метода. 1) Приводим ЗЛП к каноническому виду.
|
||||
|
Последнее изменение этой страницы: 2016-07-14; просмотров: 368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.006 с.) |


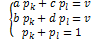 Аналогично
Аналогично 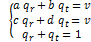
 =
=  - целевой функции, характеризующей зависимость
- целевой функции, характеризующей зависимость
 системы ограничений, состоящей из m равенств
системы ограничений, состоящей из m равенств
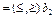 или неравенств, показывающих
или неравенств, показывающих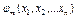
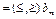
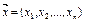 , удовлетворяющий системе ограничений (2) и естественному условию неотрицательности переменных
, удовлетворяющий системе ограничений (2) и естественному условию неотрицательности переменных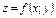
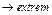 - целевая функция
- целевая функция 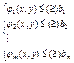 - система ограничений
- система ограничений будет часть плоскости, ограниченная линией
будет часть плоскости, ограниченная линией  . Очевидно, что решением системы неравенств будет пересечение всех их областей решений.
. Очевидно, что решением системы неравенств будет пересечение всех их областей решений.  ОДР задачи МП – общая часть областей решений всех неравенств системы ограничений.
ОДР задачи МП – общая часть областей решений всех неравенств системы ограничений.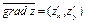 , координаты которого равны частным производным этой функции. Вектор градиент показывает направление максимального возрастания значения функции.
, координаты которого равны частным производным этой функции. Вектор градиент показывает направление максимального возрастания значения функции.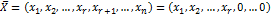 , содержащие r базисных и n-r свободных переменных.
, содержащие r базисных и n-r свободных переменных.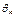 :
: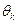 =
= 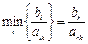 , здесь r- номер строки, в которой находится разрешающий элемент k-ого столбца.
, здесь r- номер строки, в которой находится разрешающий элемент k-ого столбца.


