
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Как получить требуемую точность расчетов, если неизвестно точное решение дифференциального уравнения?Содержание книги
Поиск на нашем сайте
На практике обычно используют правило Рунге. Если есть численные решения на двух сетках с шагом
где Для оценки погрешности расчетов любым методом поступают следующим образом: · разбивают отрезок интегрирования · вычисляют приближенное решение дифференциального уравнения на сетке · затем вычисляют приближенное решение этого уравнения на сетке · окончательным приближенным решением дифференциального уравнения считают значения - для метода Эйлера (порядок точности
- для модифицированного метода Эйлера (порядок точности
- для метода Рунге-Кутта (порядок точности
Решение обыкновенных дифференциальных уравнений В среде электронных таблиц
Рассмотрим реализацию методов решения обыкновенных дифференциальных уравнений на примере 1. Размещение информации и расчетные формулы для решения дифференциального уравнения первого порядка методом Эйлера приведены в таблицах 5 и 6, модифицированным методом Эйлера - в таблицах 7 и 8 и методом Рунге-Кутта 4-го порядка точности - в таблицах 9 и10. Таблица 5. Размещение информации
Таблица 6. Расчетные формулы метода Эйлера
Таблица 7. Размещение информации
Таблица 8. Модифицированный метод Эйлера
Таблица 9. Размещение информации
Продолжение таблицы 9
Таблица 10. Расчетные формулы метода Рунге-Кутта
Размещение информации и расчетные формулы для решения дифференциального уравнения первого порядка (пример 1) методом Эйлера в случае неизвестного точного решения приведены в таблицах 11 и 12.
Таблица 11. Размещение информации
Таблица 12. Расчетные формулы
Анализ результатов. Сравнивая результаты расчета в среде ЭТ с аналогичными расчетами по табличным алгоритмам методов, отмечаем их идентичность. Работа 4. ЗАДАЧА ОПТИМИЗАЦИИ ПРОИЗВОДСТВЕННОЙ ПРОГРАММЫ ВЫПУСКА ПРОДУКЦИИ Цель работы. Освоить методику составления математической модели задачи линейного программирования и методы ее решения. Содержание и последовательность выполнения работы 1. Изучить постановку задачи линейного программирования, графический, симплекс-метод и метод решения задачи с помощью надстройки «Поиск решения». 2. Исходные данные своего варианта представить таблицей. 3. Составить математическую модель задачи. 4. Подготовить размещение информации на рабочем листе электронной таблицы. 5. Ввести исходную информацию в память компьютера и получить оптимальный производственный план предприятия, используя надстройку «Поиск решения». 6. Решить задачу графическим методом. 7. Выполнить анализ результатов оптимизации. 8. Оформить и защитить отчет.
Краткие сведения из теории Постановка общей задачи математического программирования. Найти значения
граничным условиям
и доставляют экстремум (max или min) целевой функции
где Значения Всякий набор управляемых переменных Если ограничения (1) и целевая функция (3) линейны, то такие задачи относятся к задачам линейного программирования (ЛП). Если по смыслу управляемые переменные должны быть целыми числами, то имеем задачу целочисленного линейного программирования. Если хотя бы одно ограничение или целевая функция содержат
Математическая модель задачи оптимизации содержит три составляющие: целевую функцию, ограничения и граничные условия. Граничные условия показывают предельно допустимые значения управляемых переменных Чтобы задача имела оптимальное решение, она должна удовлетворять двум требованиям: должна быть реальная возможность иметь множество допустимых решений и должен быть принят критерий, показывающий в каком смысле принимаемое решение наилучшее. Таким образом, для постановки задачи оптимизации необходимо: · определить цель оптимизации (целевую функцию, критерий); · выбрать параметры, наиболее существенно влияющие на критерий; · выразить критерий через управляемые параметры в такой математической форме, которая с одной стороны отражала бы более точно истинное влияние каждого параметра, а с другой, обеспечивала бы наибольшую простоту предстоящего процесса оптимизации; · математически выразить все ограничения и граничные условия. Линейное программирование наиболее полно разработано к настоящему времени и довольно просто для понимания. Слово «программирование» означает, что набор управляемых переменных Эффективным методом решения задач линейного программирования является симплекс-метод, разработанный Дж. Данцигом. Основная идея метода состоит в направленном переборе некоторых вариантов решений, называемых допустимыми планами, с целью последующего их улучшения и получения оптимального плана. Число управляемых переменных характеризует размерность и сложность задачи оптимизации. Задача оптимизации производственного плана предприятия Постановка задачи. Предприятие может выпускать Требуется составить такой план выпуска продукции, который технологически осуществим по всем видам имеющихся ресурсов и приносит предприятию максимальную прибыль.
Для удобства составления математической модели исходные данные сведем в таблицу 1. Обозначим план выпуска продукции через
Таблица 1. Сводка исходных данных
Математическая модель задачи · Ограничения на объемы имеющихся ресурсов:
· Граничные условия: · Целевая функция
Рассмотрим постановку задачи ЛП и составление математической модели на простейшем примере. Пример 1. Предприятию требуется составить оптимальный по реализации суточный производственный план выпуска двух видов деталей при определенных возможностях четырех типов станков. В таблице 2 приведены: тип станков, их ресурсы, время, затрачиваемое на обработку одной детали каждого вида конкретным типом станка и прибыль от реализации одной детали каждого вида. Таблица 2. Сводка исходных данных
Обозначим Математическая модель · Ограничения на ресурсы станков:
· Граничные условия: · Дополнительные ограничения: · Целевая функция
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.78.185 (0.011 с.) |

 т.е.
т.е.  то погрешность вычислений в точке
то погрешность вычислений в точке  равна:
равна:
 - порядок точности метода;
- порядок точности метода;  - точное решение в точке
- точное решение в точке  на
на  частей;
частей; которое обозначают
которое обозначают 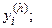
 которое обозначают
которое обозначают 
 при этом погрешность решения в точке
при этом погрешность решения в точке  )
)
 )
)
 )
)





 переменных (параметров)
переменных (параметров)  которые удовлетворяют
которые удовлетворяют 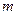 ограничениям (уравнениям или неравенствам)
ограничениям (уравнениям или неравенствам) (1)
(1)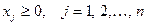 (2)
(2) (3)
(3) – известные функции;
– известные функции;  - заданные константы.
- заданные константы.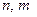 не связаны между собой.
не связаны между собой. , удовлетворяющий ограничениям и граничным условиям, определяет допустимое решение (допустимый план). Допустимое решение, при котором достигается экстремум целевой функции, называется оптимальным.
, удовлетворяющий ограничениям и граничным условиям, определяет допустимое решение (допустимый план). Допустимое решение, при котором достигается экстремум целевой функции, называется оптимальным. или произведение управляемых переменных, то имеем задачу нелинейного программирования. Если целевая функция или ограничения задаются функциями вида
или произведение управляемых переменных, то имеем задачу нелинейного программирования. Если целевая функция или ограничения задаются функциями вида  то имеем задачу геометрического программирования. Если целевая функция или ограничения зависят не только от управляемых переменных, но и параметров, то получаем задачу параметрического программирования. При наличии в математической модели элементов случайности приходим к задаче стохастического программирования. Если целевая функция и (или) система ограничений являются функциями времени или процесс получения решения имеет многошаговой характер, то имеем задачу динамического программирования.
то имеем задачу геометрического программирования. Если целевая функция или ограничения зависят не только от управляемых переменных, но и параметров, то получаем задачу параметрического программирования. При наличии в математической модели элементов случайности приходим к задаче стохастического программирования. Если целевая функция и (или) система ограничений являются функциями времени или процесс получения решения имеет многошаговой характер, то имеем задачу динамического программирования. обычно составляет программу (план) работы конкретного предприятия.
обычно составляет программу (план) работы конкретного предприятия. видов ресурсов. Известны:
видов ресурсов. Известны:  - нормы затрат
- нормы затрат  - го вида ресурса на производство единицы продукции
- го вида ресурса на производство единицы продукции  - го типа (
- го типа ( - полные объемы имеющихся ресурсов на период планирования;
- полные объемы имеющихся ресурсов на период планирования;  - прибыль, получаемая предприятием от производства и реализации единицы продукции
- прибыль, получаемая предприятием от производства и реализации единицы продукции 
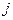



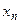







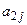

















 (4)
(4) (5)
(5) . (6)
. (6)

 - количество деталей каждого вида.
- количество деталей каждого вида.
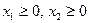 .
. ® max.
® max.


