
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кафедра прикладной математикиСодержание книги
Поиск на нашем сайте
Строительства и архитектуры
Кафедра прикладной математики
ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЭКОНОМИЧЕСКИХ ЗАДАЧ Методические указания и задания
Днепропетровск-2007 Чисельні методи розв’язання економічних задач. Методичні вказівки і завдання до практичних та лабораторних робіт. Для студентів академії усіх форм навчання / Н.М. Єршова, В.П. Скрипник, Л.В. Цибрій. – Дніпропетровськ: ПДАБА, 2007. - 108 с. – рос. мовою. Представлен набор пяти работ: интерполяция и аппроксимация таблично заданных функций; решение систем линейных алгебраических уравнений; решение обыкновенных дифференциальных уравнений; задача оптимизации производственной программы предприятия; транспортная задача. Рассмотрены методы решения задач и технология их реализации в среде электронных таблиц (приложение Excel). К каждой работе даны индивидуальные задания. Приведены методические вопросы выполнения лабораторного практикума и контрольной работы для студентов заочной и дистанционной форм обучения.
Укладачі: д.т.н., проф. Н.М.Єршова, к.ф.-м.н., доц. В.П.Скрипник, к.ф.-м.н., доц. Л.В.Цибрій
Відповідальний за випуск: Н.М.Єршова, д.т.н., професор, зав. кафедрою прикладної математики ПДАБА
Рецензент: С.М.Семенець, к.т.н., доц.
Затверждено На засіданні кафедри Прикладної математики, Протокол № 9 від 26.06 2006р
Затверждено На засіданні методичної ради ПДАБА, Протокол №3(44) від 25.01.2007р
СОДЕРЖАНИЕ Введение 4 Методические вопросы лабораторного практикума 4 Методические вопросы контрольной работы 5 Теоретические вопросы контрольной работы 7 Методические указания к решению задач 13 Работа 1. Интерполяция и аппроксимация таблично заданных функций 14 Работа 2. Решение систем линейных алгебраических уравнений 31 Работа 3. Численные методы решения обыкновенных дифференциальных уравнений 47 Работа 4. Задача оптимизации производственной программы выпуска продукции 63 Работа 5. Транспортная задача 75 Задания 87 Работа 1. Интерполяция и аппроксимация таблично заданных функций ………… 87 Работа 2. Методы решение систем линейных алгебраических уравнений 92
Работа 3. Численные методы решения обыкновенных дифференциальных уравнений 102 Работа 4. Задача оптимизации производственной программы выпуска продукции …. 103 Работа 5. Транспортная задача 105 Список рекомендуемой литературы 108 Приложение 1. Титульный лист контрольной работы 111
ВВЕДЕНИЕ
Решение прикладных задач практически всегда требует, кроме профессиональных знаний, знание методов их решения. И чаще всего эти задачи не имеют аналитического решения, особенно если объем обрабатываемой информации требует применения компьютера, а, значит, и численных методов. Современный специалист должен не только знать и уметь использовать численные методы, но и хорошо ориентироваться и правильно выбирать соответствующий численный метод, который обеспечивает наименьшую погрешность результата. Можно привести множество примеров применения матричной алгебры, методов решения линейных и нелинейных уравнений, вычисления определенных интегралов и методов статистического анализа в экономике, финансах, менеджменте, не говоря уже об инженерно-технических и научных исследованиях. Особое место в современных исследованиях занимают задачи поиска оптимального решения. Цель методических указаний – ознакомить студентов с численными методами решения некоторых видов задач и технологией их реализации в приложении Microsoft Excel. Методические указания содержат 5 работ и задания к ним для закрепления теоретического материала и выполнения контрольной работы студентами заочной и дистанционной форм обучения. МЕТОДИЧЕСКИЕ ВОПРОСЫ ЛАБОРАТОРНОГО ПРАКТИКУМА
Все задачи практических занятий решаются на компьютере, поэтому такой вид занятий правильно называть лабораторным практикумом. Цель его – закрепить теоретические знания по изучаемой дисциплине, способствовать более глубокому и детальному освоению современных компьютерных технологий, готовить студентов к умению самостоятельно решать задачи профилирующих дисциплин и курсового проектирования. К очередному практическому занятию студент должен готовиться заранее. Для этого необходимо: · ознакомиться с содержанием работы; · прочитать теоретический материал в конспекте лекций и кратких сведениях к работе;
· выяснить цель работы, четко представить себе поставленную задачу и способы ее решения; · подготовить размещение информации на рабочем листе электронной таблицы (ЭТ) На практическом занятии студент работает за компьютером, вводит исходную информацию и получает решение задачи по технологии, представленной в описании работы. По каждой работе требуется оформить отчет. Отчет выполняется в обычной тетради и должен содержать: номер работы и название, цель работы, содержание и порядок выполнения, задание, краткие теоретические сведения (без описания технологии выполнения работы), размещение информации на рабочем листе ЭТ, результаты расчета (вклейка из Excel) и анализ полученного решения. Текст должен быть написан четким и понятным почерком. Блоки алгоритмов должны соответствовать ГОСТу. При построении графиков обязательно указывать обозначение переменных и их размерности. После выполнения каждой работы проводится ее защита (зачет). Студент должен знать теорию по данной теме, технологию выполнения работы на компьютере и уметь анализировать полученные результаты. Такая защита работ должна проводиться систематически, как правило, на следующем практическом занятии. Студент, выполнивший и защитивший все работы в установленные лектором сроки, может претендовать на автоматический зачет по дисциплине.
МЕТОДИЧЕСКИЕ ВОПРОСЫ КОНТРОЛЬНОЙ РАБОТЫ
Большую роль в заочной и дистанционной формах обучения студентов имеет контрольная работа. Учебными планами специальностей экономического факультета предусмотрено выполнение контрольной работы по дисциплине «Численные методы решения экономических задач». Цель контрольной работы: ¨ Получить теоретические знания по прикладной математике и закрепить знания по информатике. ¨ Освоить методику решения задач в среде приложения Excel (надстройка «Поиск решения», мастер функций и мастер диаграмм). ¨ Развить навыки защиты выполненной работы. Содержание и объем контрольной работы Содержание – постановка и решение задач по темам: · Интерполяция и аппроксимация таблично заданных функций. · Решение систем линейных алгебраических уравнений. · Численные методы решения обыкновенных дифференциальных уравнений. · Линейное программирование. Объем - 4 задачи и один теоретический вопрос. Содержание первой, третьей и четвертой задач соответствуют работам 1, 4 и 5 данных методических указаний. Номер второй задачи выбирается по таблице 1.
Таблица 1. Номер второй задачи контрольной работы
Номер варианта теоретического вопроса и каждой задачи должен соответствовать номеру фамилии студента в списке группы. Решение задач выполняется в среде электронных таблиц (приложение Excel). Для ответа на теоретический вопрос использовать работы [1-4] и данные методические указания.
Название задач: 1. Интерполяция и аппроксимация таблично заданных функций (задача 1 контрольной работы). 2. Решение систем линейных алгебраических уравнений матричным методом. 3. Решение систем линейных алгебраических уравнений с помощью надстройки «Поиск решения». 4. Решение систем линейных алгебраических уравнений методом Гаусса. 5. Решение систем линейных алгебраических уравнений методом Зейделя. 6. Решение систем линейных алгебраических уравнений методом простой итерации. 7. Решение обыкновенного дифференциального уравнения первого порядка методом Эйлера. 8. Решение обыкновенного дифференциального уравнения первого порядка модифицированным методом Эйлера. 9. Решение обыкновенного дифференциального уравнения первого порядка методом Рунге-Кутта 4-го порядка точности. 10. Задача оптимизации производственной программы выпуска продукции (задача 3 контрольной работы). 11. Транспортная задача (задача 4 контрольной работы). Теоретические вопросы контрольной работы 1. Матричный метод решения систем линейных алгебраических уравнений (СЛАУ) и его реализация в среде ЭТ. 2. Методика решения систем линейных алгебраических уравнений в среде ЭТ с помощью надстройки «Поиск решения». 3. Решение систем линейных алгебраических уравнений методом Гаусса. 4. Реализация в среде ЭТ алгоритма метода Гаусса решения СЛАУ. 5. Табличный метод Гаусса решения систем линейных алгебраических уравнений. 6. Реализация в среде ЭТ табличного метода Гаусса решения СЛАУ. 7. Решение систем линейных алгебраических уравнений методом Зейделя. 8. Реализация в среде ЭТ алгоритма метода Зейделя решения СЛАУ. 9. Решение систем линейных алгебраических уравнений методом простой итерации. 10. Реализация в среде ЭТ алгоритма метода простой итерации решения СЛАУ. 11. Графический метод отделения корней нелинейных уравнений. 12. Аналитический метод отделения корней нелинейных уравнений. 13. Отделение корней нелинейного уравнения методом простого перебора. 14. Уточнение значений корней нелинейных уравнений методом половинного деления. 15. Реализация в среде ЭТ алгоритма метода половинного деления. 16. Уточнение значений корней нелинейных уравнений методом хорд. 17. Реализация в среде ЭТ алгоритма метода хорд. 18. Уточнение значений корней нелинейных уравнений методом касательных.
19. Реализация в среде ЭТ алгоритма метода касательных. 20. Уточнение значений корней нелинейных уравнений методом итерации. 21. Реализация в среде ЭТ алгоритма метода итераций. 22. Определение корня нелинейного уравнения в среде ЭТ с помощью надстройки «Подбор параметра». 23. Уточнение значений корней нелинейных уравнений в среде ЭТ с помощью надстройки «Поиск решения» 24. Вычисление определенных интегралов методом прямоугольников и его реализация в среде ЭТ. 25. Вычисление определенных интегралов методом трапеций и его реализация в среде ЭТ. 26. Вычисление определенных интегралов методом Симпсона и его реализация в среде ЭТ. 27. Решение обыкновенных дифференциальных уравнений первого порядка методом Эйлера. 28. Решение обыкновенных дифференциальных уравнений первого порядка методом Рунге-Кутта 4-го порядка точности 29. Реализация в среде ЭТ алгоритма метода Эйлера. 30. Реализация в среде ЭТ алгоритма метода Рунге-Кутта 4-го порядка точности. 31. Технология построения линий тренда. 32. Технология работы с надстройкой «Поиск решения» при решении систем линейных алгебраических уравнений. 31. Постановка общей задачи математического программирования. Понятие о допустимом и оптимальном решении задачи математического программирования. Требования к задаче оптимизации. 32. Постановка и математическая модель оптимизации производственной программы выпуска продукции. 33. Графический метод решения задачи ЛП. 34. Технология работы с надстройкой «Поиск решения» при решении задач линейного программирования. 35. Постановка транспортной задачи. Виды моделей транспортной задачи. Составление математической модели. 36. Решение транспортной задачи методом потенциалов. 37. Решение транспортной задачи в среде ЭТ.
Алгоритм выбора задания контрольной работы
Например, студент в списке группы записан под номером 10, предпоследняя и последняя цифры номера его зачетной книжки соответственно 3 и 6, по которым из таблицы 1 выбираем номер 5. Следовательно, ему предстоит ответить на вопрос «Реализация в среде ЭТ метода простой итерации решения СЛАУ» и решить 4 задачи: 1. Интерполяция и аппроксимация таблично заданных функций. 2. Решение СЛАУ методом Зейделя. 3. Задача оптимизации производственной программы выпуска продукции. 4. Транспортная задача Таким образом, задание варианта 10 контрольной работы имеет вид: · Теоретический вопрос «Реализация в среде ЭТ метода простой итерации решения СЛАУ».
· Задача 1. Интерполяция и аппроксимация таблично заданных функций.
Таблица 10. Значения деформации пружины в зависимости от нагрузки
· Задача 2. Решить СЛАУ методом Зейделя
· Задача 3. Составить оптимальный по реализации суточный производственный план выпуска двух видов деталей при определенных возможностях четырех типов станков. В таблице 1 приведены: типы станков, время, затрачиваемое каждым станком на обработку одной детали каждого вида, ресурсы станков в сутки и прибыль от реализации одной детали каждого вида.
Таблица 1. Сводка исходных данных
· Задача 4. Постановка задачи. Имеется три пункта производства Для удобства составления математической модели исходные данные сведены в таблицу 1, где обозначено
Таблица 1. Сводка исходных данных
Примечание. Варианты задач приведены в заданиях к соответствующим работам данных методических указаний.
Содержание описательной части контрольной работы: ¨ Титульный лист (приложение 1); ¨ Задание на контрольную работу; ¨ Название теоретического вопроса и ответ на него в краткой форме; ¨ Далее по каждой задаче: Þ краткие сведения из теории; Þ размещение информации на рабочем листе ЭТ; Þ результаты решения задачи (вставка из Excel); Þ анализ полученных результатов. ¨ Список использованной литературы.
Оформление контрольной работы Контрольная работа – основной документ, необходимый студенту для получения зачета по данной дисциплине. Она отражает основные этапы работы и полученные результаты. Общими требованиями к оформлению контрольной работы являются: · четкость и логическая последовательность изложения материала; · убедительность аргументации; · краткость и точность формулировок; · конкретность изложения результатов работы. Контрольную работу можно представлять на украинском или русском языках, оформленную в тетради вручную. Графики, диаграммы и таблицы, созданные в среде ЭТ, распечатываются и затем вклеиваются в работу. Список использованной литературы оформляется аналогично тому, как это сделано в данной работе. Контрольная работа должна быть оформлена в отдельной тетради. Следует иметь в виду, что небрежно оформленная контрольная работа студента может быть не допущена к защите. ТАБЛИЧНО ЗАДАННЫХ ФУНКЦИЙ Цель работы: ¨ Ознакомиться с различными способами приближения функций (интерполяция, сплайн-интерполяция, аппроксимация). ¨ Практическиосвоить метод наименьших квадратов (МНК) и технологию работы с надстройкой «Поиск решения». ¨ Изучить технологию построения линий тренда. Содержание и порядок выполнения работы 1. Изучить постановку задачи интерполяции таблично заданных функций и ее решение с помощью многочлена Лагранжа. 2. Изучить постановку задачи аппроксимации таблично заданных функций и ее решение с помощью метода наименьших квадратов. 3. Из заданий к данной работе записать таблицу исходных данных своего варианта. 4. Подготовить размещение информации на рабочем листе электронных таблиц (ЭТ) для определения коэффициентов интерполяционного многочлена Лагранжа по первым трем узловым точкам заданной таблицы. 5. В среде ЭТ ввести исходные данные, расчетные формулы, получить значения коэффициентов многочлена Лагранжа и определить значение функции 6. Записать интерполяционный многочлен Лагранжа с конкретными значениями коэффициентов и полученное значение функции 7. Подготовить размещение информации на рабочем листе электронных таблиц (ЭТ) для определения коэффициентов аппроксимирующей функции с помощью метода наименьших квадратов. 8. В среде ЭТ реализовать МНК с помощью надстройки «Поиск решения» и вычислить среднеквадратическую погрешность аппроксимации. 9. Записать аппроксимирующую функцию 10. С помощью мастера диаграмм построить точечную диаграмму функции 11. Записать аппроксимирующую функцию, полученную путем построения линии тренда. 12. Выполнить анализ результатов расчета на основе сравнения выражений аппроксимирующих функций, полученных в пунктах 9 и 11. 13. Оформить и защитить отчет.
Краткие сведения из теории
Большинство численных методов основано на замене сложных объектов, уравнений и функций более простыми. Наиболее удобной функцией является алгебраический многочлен. Для его задания требуется конечное число коэффициентов, его легко дифференцировать, интегрировать и просто вычислять значения многочлена. Поэтому алгебраические многочлены широко применяются для приближения функций. Пусть известны значения некоторой функции
Эти значения могут быть получены из эксперимента или найдены путем достаточно сложных вычислений. Возникает задача приближенного восстановления функции
и называется интерполяционным. Точки
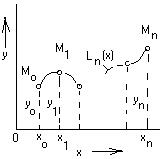
Геометрически это означает, что нужно подобрать алгебраический многочлен Приближенное восстановление функции
Рис.1. Геометрический смысл интерполяции
Приведем способ конструирования и вид многочлена Лагранжа для случая трех узлов интерполяции. Многочлен Лагранжа
Легко видеть, что при Пример 1. Найти многочлен Лагранжа, принимающий в данных точках заданные значения (таблица 1).
Таблица 1. Узловые точки
Решение. Так как имеем три узла интерполяции, то общий вид многочлена Лагранжа соответствует записи
где
Расчет коэффициентов
Таблица 2. Размещение информации на рабочем листе ЭТ
Таблица 3. Расчетные формулы
В результате расчетов получили алгебраический многочлен Лагранжа Пример 2. Используя полученную в примере 1 формулу, найти значение функции Решение. В соответствии с методом интерполяции восстанавливаемая функция В ячейку F4 записана формула =$h$17+$h$16*e4+$h$15*e4^2. С ростом числа узлов интерполяции и соответственно степени интерполяционного многочлена увеличивается погрешность, поэтому используют способ приближения функций с помощью сплайнов (гладких функций, составленных из конечного числа алгебраических многочленов). Сплайном называется функция, которая вместе с несколькими производными непрерывна на всем заданном отрезке
Таким образом, при сплайн-интерполяции определяется алгебраический многочлен для каждого элементарного отрезка в отличие от интерполяции, когда задается алгебраический многочлен для всего отрезка
Рис.2. Линейная сплайн-интерполяция
На практике наиболее распространены сплайны третьей степени, т.е. кубическая сплайн-интерполяция. Кубический сплайн имеет непрерывную кривизну, что исключает разрыв первой производной в узлах интерполяции. Точность приближения функции Основной недостаток интерполяционных многочленов – наличие большого числа экстремумов и точек перегибов. Если представить таблично заданные значения функции В математике замена истинной зависимости
Возникает задача определения коэффициентов ¨ на плоскости ¨ записывается разность между значениями аппроксимирующей функции и таблично заданной функции
Рис.3. Геометрический смысл аппроксимации
¨ в методе наименьших квадратов минимизируют сумму квадратов отклонений по всем таблично заданным ¨ так как ¨ имеем функцию многих переменных. Необходимое условие минимума такой функции заключается в равенстве нулю всех ее первых частных производных, т.е. ¨ точность аппроксимации определяется среднеквадратичной погрешностью Примечание. Условие минимума суммы самих отклонений, а не их квадратов, не решает проблемы, так как сумма отклонений Таким образом, в задаче аппроксимации требуется определить такие значения В терминах программы «Поиск решения» функция Пример 3. Найти аппроксимирующую функцию по таблично заданным значениям
Решение. С помощью мастера диаграмм строим точечную диаграмму (рис.4). По расположению точек на плоскости можно предположить параболическую зависимость между
Коэффициенты
Рис.4. График таблично заданной функции В таблице 4 представлено размещение информации и результаты решения, в таблице 5 приведены расчетные формулы.
Таблица 4. Результаты решения
Таблица 5. Расчетные формулы
Чтобы использовать надстройку «Поиск решения» для решения этой задачи, необходимо предварительно выполнить следующие действия: 1. Выбрать на рабочем листе ЭТ ячейки, в которых будут размещены исходные данные и результаты решения задачи (см. таблицу 4). Как видно, исходные данные расположены в ячейках: значения аргумента | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 , мм
, мм

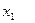

 с заданными объемами производства некоторой однородной продукции 25, 55, 22 и четыре пункта потребления
с заданными объемами производства некоторой однородной продукции 25, 55, 22 и четыре пункта потребления  с заданными объемами потребления 45, 15, 22, 20 этой продукции. Известны
с заданными объемами потребления 45, 15, 22, 20 этой продукции. Известны  - затраты на транспортировку единицы продукции из
- затраты на транспортировку единицы продукции из  -го пункта производства в
-го пункта производства в 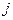 - й пункт потребления (
- й пункт потребления ( ). Требуется составить такой план перевозок
). Требуется составить такой план перевозок  , чтобы суммарные затраты на транспортировку были минимальными и были удовлетворены потребности во всех пунктах потребления.
, чтобы суммарные затраты на транспортировку были минимальными и были удовлетворены потребности во всех пунктах потребления.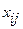 - количество единиц продукции, перевозимой из
- количество единиц продукции, перевозимой из 
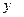 для произвольного значения
для произвольного значения  внутри отрезка интерполяции.
внутри отрезка интерполяции. с полученными параметрами.
с полученными параметрами.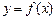 и линию тренда.
и линию тренда. в
в  различных точках
различных точках  которые обозначим в виде:
которые обозначим в виде:
 Часто для решения этой задачи строится алгебраический многочлен
Часто для решения этой задачи строится алгебраический многочлен  степени
степени  который в точках
который в точках  принимает заданные значения, т.е.
принимает заданные значения, т.е.
 называются узлами интерполяции. Следовательно, задача интерполяции ставится в следующей форме: найти алгебраический многочлен
называются узлами интерполяции. Следовательно, задача интерполяции ставится в следующей форме: найти алгебраический многочлен 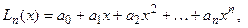 график которого проходит через заданную систему точек
график которого проходит через заданную систему точек 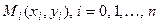 (рис.1).
(рис.1). называется интерполяцией функции с помощью алгебраического многочлена. Если точка
называется интерполяцией функции с помощью алгебраического многочлена. Если точка  то операция замены функции называется интерполированием в узком смысле. Экстраполированием функции называют операцию в случае, если точка
то операция замены функции называется интерполированием в узком смысле. Экстраполированием функции называют операцию в случае, если точка 
 имеет степень не выше двух и вид:
имеет степень не выше двух и вид: .
. Сомножителем перед
Сомножителем перед  является дробь, в числителе которой находится многочлен из произведения разностей
является дробь, в числителе которой находится многочлен из произведения разностей  В знаменателе находится многочлен числителя, рассчитанный в точке
В знаменателе находится многочлен числителя, рассчитанный в точке  Дроби эти называются коэффициентами Лагранжа и обозначаются
Дроби эти называются коэффициентами Лагранжа и обозначаются 
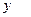
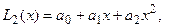 (2)
(2)
 выполним в среде ЭТ. Размещение информации представлено в таблице 2, расчетные формулы приведены в таблице 3.
выполним в среде ЭТ. Размещение информации представлено в таблице 2, расчетные формулы приведены в таблице 3.
 значения которого совпадают со значениями заданной функции в узловых точках.
значения которого совпадают со значениями заданной функции в узловых точках.
 В таблице 2 выполнен расчет
В таблице 2 выполнен расчет  следовательно,
следовательно, 
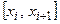 в отдельности является некоторым алгебраическим многочленом. На рис.2 изображен график линейной сплайн-интерполяции. Сплайн
в отдельности является некоторым алгебраическим многочленом. На рис.2 изображен график линейной сплайн-интерполяции. Сплайн  задается в виде:
задается в виде: (3)
(3)
 , близко расположенную к заданному множеству табличных точек.
, близко расположенную к заданному множеству табличных точек. некоторой приближенной
некоторой приближенной  (4)
(4) этого многочлена наилучшим образом, т.е. установления таких значений параметров
этого многочлена наилучшим образом, т.е. установления таких значений параметров  графически изображаются таблично заданные точки и аппроксимирующая функция;
графически изображаются таблично заданные точки и аппроксимирующая функция; для каждого таблично заданного
для каждого таблично заданного  (рис.3):
(рис.3):  называемая отклонением аппроксимирующей функции от соответствующего табличного значения;
называемая отклонением аппроксимирующей функции от соответствующего табличного значения;
 где
где  - количество таблично заданных точек;
- количество таблично заданных точек; известны (заданы таблицей), то сумма квадратов отклонений есть функция параметров
известны (заданы таблицей), то сумма квадратов отклонений есть функция параметров  Тогда математическая запись метода наименьших квадратов имеет вид:
Тогда математическая запись метода наименьших квадратов имеет вид:  (5)
(5)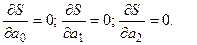
 (6)
(6) может быть очень малой и тогда, когда отдельные отклонения очень велики, но имеют разные знаки и взаимно компенсируют друг друга.
может быть очень малой и тогда, когда отдельные отклонения очень велики, но имеют разные знаки и взаимно компенсируют друг друга.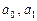 и
и 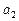 , при которых функция
, при которых функция  достигает минимума. Это обычная задача определения экстремума функции трех переменных без ограничений и может быть решена средствами надстройки Excel «Поиск решения».
достигает минимума. Это обычная задача определения экстремума функции трех переменных без ограничений и может быть решена средствами надстройки Excel «Поиск решения». (квадратная парабола). Запишем общий вид аппроксимирующей функции:
(квадратная парабола). Запишем общий вид аппроксимирующей функции:
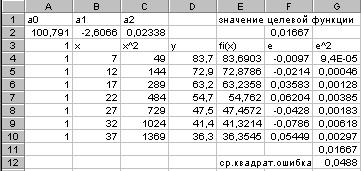


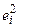


 - в ячейках B4:B10; значения функции
- в ячейках B4:B10; значения функции 


