
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Защита контрольной работы и сдача зачетаСодержание книги
Поиск на нашем сайте
Контрольная работа сдается для проверки на кафедру “Прикладная математика” и после допуска к защите - защищается в процессе собеседования студента с преподавателем, проверяющим работу. При этом студенту задаются любые вопросы по содержанию контрольной работы. После защиты контрольной работы студент допускается к сдаче зачета. Вопросы к зачету соответствуют контрольным вопросам данных методических указаний. Зачет принимает лектор данной дисциплины. При подготовке к защите контрольной работы и зачету следует использовать рекомендуемую литературу и данные методические указания. Методические указания к решению задач Задача 1. Требуется построить для данных своего варианта (см. задания к работе 1 данных методических указаний) уравнение интерполяционного многочлена Лагранжа (по первым трем узловым точкам) и определить его значение в любой промежуточной точке. Кроме того, получить аппроксимирующую функцию с помощью метода наименьших квадратов и методом построения линии тренда. Содержание, последовательность решения, краткие сведения из теории и компьютерной технологии приведены в работе 1. Задачи 2-6. Требуетсярешить систему линейных алгебраических уравнений своего варианта (см. задания к работе 2 данных методических указаний). Содержание, последовательность решения, краткие сведения из теории и компьютерной технологии приведены в работе 2.
Задачи 7-9. Требуетсярешить обыкновенное дифференциальное уравнение первого порядка своего варианта (см. задания к работе 3 данных методических указаний) заданным методом. Содержание, последовательность решения, краткие сведения из теории и компьютерной технологии приведены в работе 3. Задача 10. Требуется определить оптимальный производственный план предприятия для данных своего варианта (см. задания к работе 4 данных методических указаний) графическим методом и с помощью надстройки «Поиск решения». Содержание, последовательность решения задачи, краткие сведения из теории, компьютерной технологии приведены в работе 4. Задача 11. Требуется определить оптимальный план перевозок для своего варианта (см. задания к работе 5 данных методических указаний) методом потенциалов и с помощью надстройки «Поиск решения». Содержание, последовательность решения, краткие сведения из теории приведены в работе 5.
Работа 1. ИНТЕРПОЛЯЦИЯ И АППРОКСИМАЦИЯ ТАБЛИЧНО ЗАДАННЫХ ФУНКЦИЙ Цель работы: ¨ Ознакомиться с различными способами приближения функций (интерполяция, сплайн-интерполяция, аппроксимация). ¨ Практическиосвоить метод наименьших квадратов (МНК) и технологию работы с надстройкой «Поиск решения». ¨ Изучить технологию построения линий тренда. Содержание и порядок выполнения работы 1. Изучить постановку задачи интерполяции таблично заданных функций и ее решение с помощью многочлена Лагранжа. 2. Изучить постановку задачи аппроксимации таблично заданных функций и ее решение с помощью метода наименьших квадратов. 3. Из заданий к данной работе записать таблицу исходных данных своего варианта. 4. Подготовить размещение информации на рабочем листе электронных таблиц (ЭТ) для определения коэффициентов интерполяционного многочлена Лагранжа по первым трем узловым точкам заданной таблицы. 5. В среде ЭТ ввести исходные данные, расчетные формулы, получить значения коэффициентов многочлена Лагранжа и определить значение функции 6. Записать интерполяционный многочлен Лагранжа с конкретными значениями коэффициентов и полученное значение функции 7. Подготовить размещение информации на рабочем листе электронных таблиц (ЭТ) для определения коэффициентов аппроксимирующей функции с помощью метода наименьших квадратов. 8. В среде ЭТ реализовать МНК с помощью надстройки «Поиск решения» и вычислить среднеквадратическую погрешность аппроксимации. 9. Записать аппроксимирующую функцию 10. С помощью мастера диаграмм построить точечную диаграмму функции 11. Записать аппроксимирующую функцию, полученную путем построения линии тренда. 12. Выполнить анализ результатов расчета на основе сравнения выражений аппроксимирующих функций, полученных в пунктах 9 и 11. 13. Оформить и защитить отчет.
Краткие сведения из теории
Большинство численных методов основано на замене сложных объектов, уравнений и функций более простыми. Наиболее удобной функцией является алгебраический многочлен. Для его задания требуется конечное число коэффициентов, его легко дифференцировать, интегрировать и просто вычислять значения многочлена. Поэтому алгебраические многочлены широко применяются для приближения функций. Пусть известны значения некоторой функции
Эти значения могут быть получены из эксперимента или найдены путем достаточно сложных вычислений. Возникает задача приближенного восстановления функции
и называется интерполяционным. Точки
Геометрически это означает, что нужно подобрать алгебраический многочлен Приближенное восстановление функции
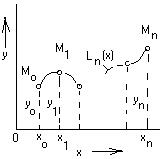
Рис.1. Геометрический смысл интерполяции
Приведем способ конструирования и вид многочлена Лагранжа для случая трех узлов интерполяции. Многочлен Лагранжа
Легко видеть, что при Пример 1. Найти многочлен Лагранжа, принимающий в данных точках заданные значения (таблица 1).
Таблица 1. Узловые точки
Решение. Так как имеем три узла интерполяции, то общий вид многочлена Лагранжа соответствует записи
где
Расчет коэффициентов
Таблица 2. Размещение информации на рабочем листе ЭТ
Таблица 3. Расчетные формулы
В результате расчетов получили алгебраический многочлен Лагранжа Пример 2. Используя полученную в примере 1 формулу, найти значение функции Решение. В соответствии с методом интерполяции восстанавливаемая функция В ячейку F4 записана формула =$h$17+$h$16*e4+$h$15*e4^2. С ростом числа узлов интерполяции и соответственно степени интерполяционного многочлена увеличивается погрешность, поэтому используют способ приближения функций с помощью сплайнов (гладких функций, составленных из конечного числа алгебраических многочленов). Сплайном называется функция, которая вместе с несколькими производными непрерывна на всем заданном отрезке
Таким образом, при сплайн-интерполяции определяется алгебраический многочлен для каждого элементарного отрезка в отличие от интерполяции, когда задается алгебраический многочлен для всего отрезка
Рис.2. Линейная сплайн-интерполяция
На практике наиболее распространены сплайны третьей степени, т.е. кубическая сплайн-интерполяция. Кубический сплайн имеет непрерывную кривизну, что исключает разрыв первой производной в узлах интерполяции. Точность приближения функции Основной недостаток интерполяционных многочленов – наличие большого числа экстремумов и точек перегибов. Если представить таблично заданные значения функции В математике замена истинной зависимости
Возникает задача определения коэффициентов ¨ на плоскости ¨ записывается разность между значениями аппроксимирующей функции и таблично заданной функции
Рис.3. Геометрический смысл аппроксимации
¨ в методе наименьших квадратов минимизируют сумму квадратов отклонений по всем таблично заданным ¨ так как ¨ имеем функцию многих переменных. Необходимое условие минимума такой функции заключается в равенстве нулю всех ее первых частных производных, т.е. ¨ точность аппроксимации определяется среднеквадратичной погрешностью Примечание. Условие минимума суммы самих отклонений, а не их квадратов, не решает проблемы, так как сумма отклонений Таким образом, в задаче аппроксимации требуется определить такие значения В терминах программы «Поиск решения» функция Пример 3. Найти аппроксимирующую функцию по таблично заданным значениям
Решение. С помощью мастера диаграмм строим точечную диаграмму (рис.4). По расположению точек на плоскости можно предположить параболическую зависимость между
Коэффициенты
Рис.4. График таблично заданной функции В таблице 4 представлено размещение информации и результаты решения, в таблице 5 приведены расчетные формулы.
Таблица 4. Результаты решения
Таблица 5. Расчетные формулы
Чтобы использовать надстройку «Поиск решения» для решения этой задачи, необходимо предварительно выполнить следующие действия: 1. Выбрать на рабочем листе ЭТ ячейки, в которых будут размещены исходные данные и результаты решения задачи (см. таблицу 4). Как видно, исходные данные расположены в ячейках: значения аргумента 2. Ввести в выбранные ячейки исходные данные и расчетные формулы согласно таблице 5. 3. Если для формулы указан диапазон ячеек, то формулу после записи следует скопировать в остальные ячейки этого диапазона. Примечание. Размещение информации на рабочем листе зависит от автора решаемой задачи и оно может отличаться от приведенного выше.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 205; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.42.25 (0.009 с.) |

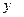 для произвольного значения
для произвольного значения  внутри отрезка интерполяции.
внутри отрезка интерполяции. с полученными параметрами.
с полученными параметрами.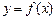 и линию тренда.
и линию тренда. в
в  различных точках
различных точках  которые обозначим в виде:
которые обозначим в виде:
 Часто для решения этой задачи строится алгебраический многочлен
Часто для решения этой задачи строится алгебраический многочлен  степени
степени  который в точках
который в точках  принимает заданные значения, т.е.
принимает заданные значения, т.е.
 называются узлами интерполяции. Следовательно, задача интерполяции ставится в следующей форме: найти алгебраический многочлен
называются узлами интерполяции. Следовательно, задача интерполяции ставится в следующей форме: найти алгебраический многочлен 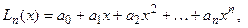 график которого проходит через заданную систему точек
график которого проходит через заданную систему точек 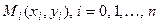 (рис.1).
(рис.1). называется интерполяцией функции с помощью алгебраического многочлена. Если точка
называется интерполяцией функции с помощью алгебраического многочлена. Если точка  то операция замены функции называется интерполированием в узком смысле. Экстраполированием функции называют операцию в случае, если точка
то операция замены функции называется интерполированием в узком смысле. Экстраполированием функции называют операцию в случае, если точка 
 имеет степень не выше двух и вид:
имеет степень не выше двух и вид: .
. Сомножителем перед
Сомножителем перед  является дробь, в числителе которой находится многочлен из произведения разностей
является дробь, в числителе которой находится многочлен из произведения разностей  В знаменателе находится многочлен числителя, рассчитанный в точке
В знаменателе находится многочлен числителя, рассчитанный в точке  Дроби эти называются коэффициентами Лагранжа и обозначаются
Дроби эти называются коэффициентами Лагранжа и обозначаются 
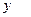
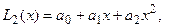 (2)
(2)
 выполним в среде ЭТ. Размещение информации представлено в таблице 2, расчетные формулы приведены в таблице 3.
выполним в среде ЭТ. Размещение информации представлено в таблице 2, расчетные формулы приведены в таблице 3.
 значения которого совпадают со значениями заданной функции в узловых точках.
значения которого совпадают со значениями заданной функции в узловых точках.
 В таблице 2 выполнен расчет
В таблице 2 выполнен расчет  следовательно,
следовательно, 
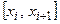 в отдельности является некоторым алгебраическим многочленом. На рис.2 изображен график линейной сплайн-интерполяции. Сплайн
в отдельности является некоторым алгебраическим многочленом. На рис.2 изображен график линейной сплайн-интерполяции. Сплайн  задается в виде:
задается в виде: (3)
(3)
 , близко расположенную к заданному множеству табличных точек.
, близко расположенную к заданному множеству табличных точек. некоторой приближенной
некоторой приближенной  (4)
(4) этого многочлена наилучшим образом, т.е. установления таких значений параметров
этого многочлена наилучшим образом, т.е. установления таких значений параметров  графически изображаются таблично заданные точки и аппроксимирующая функция;
графически изображаются таблично заданные точки и аппроксимирующая функция; для каждого таблично заданного
для каждого таблично заданного  (рис.3):
(рис.3):  называемая отклонением аппроксимирующей функции от соответствующего табличного значения;
называемая отклонением аппроксимирующей функции от соответствующего табличного значения;
 где
где  - количество таблично заданных точек;
- количество таблично заданных точек; известны (заданы таблицей), то сумма квадратов отклонений есть функция параметров
известны (заданы таблицей), то сумма квадратов отклонений есть функция параметров  Тогда математическая запись метода наименьших квадратов имеет вид:
Тогда математическая запись метода наименьших квадратов имеет вид:  (5)
(5)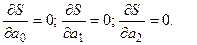
 (6)
(6) может быть очень малой и тогда, когда отдельные отклонения очень велики, но имеют разные знаки и взаимно компенсируют друг друга.
может быть очень малой и тогда, когда отдельные отклонения очень велики, но имеют разные знаки и взаимно компенсируют друг друга.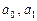 и
и 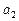 , при которых функция
, при которых функция  достигает минимума. Это обычная задача определения экстремума функции трех переменных без ограничений и может быть решена средствами надстройки Excel «Поиск решения».
достигает минимума. Это обычная задача определения экстремума функции трех переменных без ограничений и может быть решена средствами надстройки Excel «Поиск решения». (квадратная парабола). Запишем общий вид аппроксимирующей функции:
(квадратная парабола). Запишем общий вид аппроксимирующей функции:
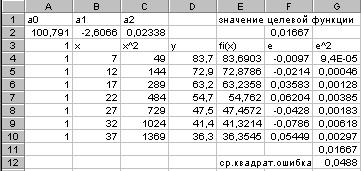


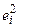


 - в ячейках B4:B10; значения функции
- в ячейках B4:B10; значения функции  - в ячейках D4:D10; значения коэффициентов
- в ячейках D4:D10; значения коэффициентов 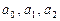 аппроксимирующего многочлена - в ячейках A2:C2 (до применения метода оптимизации эти ячейки будут пустыми); значение целевой функции
аппроксимирующего многочлена - в ячейках A2:C2 (до применения метода оптимизации эти ячейки будут пустыми); значение целевой функции  в ячейке F2 (до применения метода оптимизации в этой ячейке будет
в ячейке F2 (до применения метода оптимизации в этой ячейке будет  ); среднеквадратическая погрешность
); среднеквадратическая погрешность  - в ячейке G12. Кроме того, на рабочем листе отведены ячейки для вспомогательных величин: ячейки C4:C10 - для значений
- в ячейке G12. Кроме того, на рабочем листе отведены ячейки для вспомогательных величин: ячейки C4:C10 - для значений  ; ячейки E4:E10 - для значений аппроксимирующей функции
; ячейки E4:E10 - для значений аппроксимирующей функции  в точках
в точках  значений аппроксимирующей функции от табличных значений
значений аппроксимирующей функции от табличных значений 


