
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Путем построения линий трендаСодержание книги
Поиск на нашем сайте
1. Построить точечную диаграмму функции 2. Щелкнуть мышью на любой точке диаграммы. Все узловые точки выделятся квадратиками. 3. Войти в меню Диаграмма и выбрать операцию Добавить линию тренда. Откроется диалоговое окно Линия тренда (рис.8). Из предлагаемых видов аппроксимирующих функций выбрать полином 2-го порядка. 4. Для получения на диаграмме аналитического выражения аппроксимирующей функции необходимо в этом же окне (рис.8) щелкнуть на кнопке Параметры и в открывшемся окне (рис.9) установить флажки в поле Показывать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации. Щелкнуть на кнопке ОК.
В итоге на диаграмме (рис.10) появится уравнение аппроксимирующей функции и значение достоверности аппроксимации 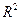 . Чем ближе это значение к единице, тем точнее аппроксимация. . Чем ближе это значение к единице, тем точнее аппроксимация.
Рис. 8. Диалоговое окно Линия тренда
Рис.9. Вкладка Параметры Примечание. В программе «Линия тренда» используется метод наименьших квадратов.
Рис. 10. Линия тренда
Таким образом, уравнение аппроксимирующей функции, полученное путем построения линии тренда, имеет вид:
Сравнивая уравнения (7) и (8), отмечаем их хорошее совпадение. Работа 2. МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Цель работы:Освоить методы решения систем линейных алгебраических уравнений (СЛАУ) и компьютерныетехнологии их реализации. Содержание и порядок выполнения работы 1. Записать системы линейных алгебраических уравнений своего варианта. 2. Изучить метод Гаусса решения СЛАУ. 3. Подготовить размещение информации на рабочем листе ЭТ для реализации метода Гаусса. 4. Получить решение на компьютере и занести результаты в соответствующие ячейки размещения информации (пункт 3). 5. Представить СЛАУ в матричной форме и получить формулу ее решения матричным методом. 6. Подготовить размещение информации на рабочем листе ЭТ для реализации матричного метода.
7. Получить решение на компьютере и занести результаты в соответствующие ячейки размещения информации (пункт 6). 8. Подготовить размещение информации на рабочем листе ЭТ для решения заданой системы линейных алгебраических уравнений с помощью надстройки «Поиск решения». 9. Получить решение на компьютере и занести результаты в соответствующие ячейки размещения информации (пункт 8). 10. Решить СЛАУ методами простой итерации и Зейделя. 11. Выполнить анализ полученных решений. 12. Оформить и защитить отчет Краткие сведения из теории И компьютерной технологии Методы решения систем линейных алгебраических уравнений разбиваются на две группы. К первой группе относятся прямые или точные методы, алгоритмы которых позволяют получить решение системы за конечное число арифметических действий. Метод Гаусса относится к точным методам. Вторую группу составляют приближенные или итерационные методы. К этой группе относятся методы простой итерации и Зейделя. Наличие в приложении Excel матричных функций (мастер функций) и надстройки «Поиск решения» позволяет значительно упростить технологию и ускорить процесс получения решения систем линейных алгебраических уравнений.
Метод Гаусса решения СЛАУ Метод Гаусса применяется к решению систем общего вида с плотно заполненной матрицей. Суть метода Гаусса состоит в последовательном исключении неизвестных путем приведения системы к треугольному виду (прямой ход) и последующего решения полученной системы, начиная с последнего уравнения с одним неизвестным (обратный ход). Метод Гаусса неприменим, если на главной диагонали оказывается нулевой элемент. В этом случае необходимо предварительно переставить (поменять местами) уравнения. Устойчивость метода снижается, если на главной диагонали расположен близкий к нулю элемент, что приводит к значительной погрешности. Избежать этого можно также перестановкой уравнений. Для контроля результатов расчета необходимо найти невязки, т.е. разности между левой и правой частью каждого уравнения:
или в развернутом виде:
где
Решение СЛАУ методом Гаусса удобно реализовать в приложении Excel, используя пошаговое программирование. Пример 1. Решить заданную систему линейных алгебраических уравнений методом Гаусса
Размещение информации на рабочем листе ЭТ в рассматриваемом случае (т.е. системы четырех уравнений с четырьмя неизвестными) может выполняться, как показано в таблице 1.
Таблица 1. Размещение информации на рабочем листе ЭТ
Как видно из таблицы 1, элементы Результаты решения системы (3) методом Гаусса приведены в таблицах 2 и 3.
Таблица 2. Прямой ход метода Гаусса
Таблица 3. Обратный ход метода Гаусса
Анализ результатов. В результате решения получены следующие значения корней заданной системы уравнений:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 294; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.141.244 (0.01 с.) |

 с помощью мастера диаграмм (следует указать реальные значения элементов массива Х). Так как массивы исходных данных находятся в несмежных диапазонах ячеек, то необходимо выделить вместе с заголовком вначале массив Х, затем нажать клавишу Ctrl и, не отпуская ее, выделить мышью массив Y.
с помощью мастера диаграмм (следует указать реальные значения элементов массива Х). Так как массивы исходных данных находятся в несмежных диапазонах ячеек, то необходимо выделить вместе с заголовком вначале массив Х, затем нажать клавишу Ctrl и, не отпуская ее, выделить мышью массив Y.
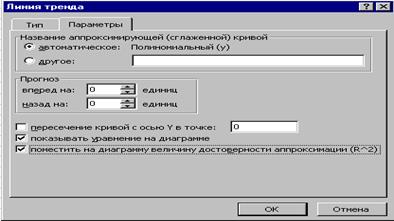

 (8)
(8)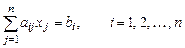
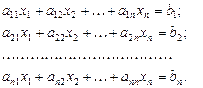 (1)
(1) , (2)
, (2) - найденные значения неизвестных;
- найденные значения неизвестных;  - свободные коэффициенты;
- свободные коэффициенты;  - элементы матрицы системы;
- элементы матрицы системы;  - невязки.
- невязки. (3)
(3) вычисляются по формулам, которые следует ввести в диапазон ячеек B24:B27. В ячейку B30 вводится формула для вычисления невязки
вычисляются по формулам, которые следует ввести в диапазон ячеек B24:B27. В ячейку B30 вводится формула для вычисления невязки  , которая копируется в диапазон ячеек B31:B33.
, которая копируется в диапазон ячеек B31:B33.

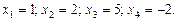 Невязки равны нулю, следовательно, требуемая точность расчета достигнута.
Невязки равны нулю, следовательно, требуемая точность расчета достигнута.


