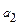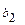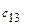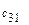Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Работа 2. Методы решения систем линейныхСодержание книги
Поиск на нашем сайте
АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ Согласно порядковому номеру в журнале выбрать систему уравнений и решить ее в среде ЭТ методом Гаусса, матричным методом и с помощью надстройки «Поиск решения». 1.
2.
3.
4.
5.
6. 7.
8.
9.
10.
11.
12. 13.
14.
15.
16.
17.
18. 19.
20.
21.
22.
23.
24. 25.
26.
27.
28.
29.
30. 31.
32.
33.
34.
35.
Согласно порядковому номеру в журнале, выбрать систему уравнений и решить ее в среде ЭТ методами простой итерации и Зейделя. 1.
3.
5.
7.
9. 11.
13.
15.
17.
19. 21.
23.
25.
27.
29.
Работа 3. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Решить дифференциальное уравнение своего варианта методом Эйлера, модифицированным методом Эйлера, методом Рунге-Кутта 4-го порядка точности и построить на одном рисунке с помощью мастера диаграмм графики полученных функций. Варианты заданий приведены в таблице 1.
Таблица 1. Дифференциальные уравнения первого порядка
Работа 4. ЗАДАЧА ОПТИМИЗАЦИИ ПРОИЗВОДСТВЕННОЙ ПРОГРАММЫ ВЫПУСКА ПРОДУКЦИИ
Предприятию требуется составить оптимальный по реализации суточный производственный план выпуска двух видов деталей при определенных возможностях четырех типов станков. Исходные данные всех вариантов приведены в таблице 2. Данные своего варианта необходимо предварительно свести в таблицу 1.
Таблица 1. Сводка исходных данных
Обозначения:
Таблица 2. Варианты заданий
Работа 5. ТРАНСПОРТНАЯ ЗАДАЧА
Постановка задачи. Имеется три пункта производства Для удобства составления математической модели исходные данные необходимо свести в таблицу 1, где обозначено
Таблица 1. Сводка исходных данных
Таблица 2. Объемы производства и потребления
Таблица 3. Элементы матрицы затрат
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Ершова Н.М., Цыбрий Л.В, Скрипник В.П..Численные методы решения задач. Дистанционный курс по дисциплине «Численные методы решения экономических задач». – Днепропетровск: ПГАСА, 2004. – 118 с. 2. Ершова Н.М., Цыбрий Л.В, Скрипник В.П..Численные методы решения экономических и инженерных задач. Методические указания. – Днепропетровск: ПГАСА, 2002. – 72 с. 3. Єршова Н.М., Цибрій Л.В., Скрипник В.П..Чисельні методи розв’язання економічних і інженерних задач. Методичні вказівки. – Дніпропетровськ: ПДАБА, 2003. – 72 с. 4. Цибрій Л.В. Дослідження операцій. Методичні вказівки. – Дніпропетровськ: ПДАБА, 2005. –41 с. 5. Ершова Н.М. Компьютерные технологии реализации математических методов управления производством: Конспект лекций. – Днепропетровск: ПГАСА, 2001. – 93 с. 6. Ершова Н.М. Задания к самостоятельной работе по дисциплине «Численные методы решения экономических задач». – Днепропетровск: ПГАСА, 2003. – 16 с. 7. Вычислительная техника в инженерных и экономических расчетах/ Под ред. А.В. Петрова. – М.: Высшая школа, 1984. – 320 с. 8. Копченова Н.В., Марон И.А. Вычислительная математика в примерах и задачах. – М.: Наука, 1972. – 367 с.
9. Вершинин О.Е. Компьютер для менеджера: Учеб. Пособие для экон. спец. Вузов. – М.: Высш. шк., 1990. – 240 с. 10. Колесников А.Н. Краткий курс математики для экономистов: Учеб. пособие. – М.: Высшее образование, 2000. – 208 с. 11. Уотшем Т. Дж., Паррамоу К. Количественные методы в финансах: Учеб. пособие для вузов/ Пер. с англ. Под ред. М.Р. Ефимовой. – М.: Финансы, ЮНИТИ, 1999. – 527 с. 12. Цибрій Л.В., Скрипник В.П. Методичні вказівки до застосування чисельних методів для розв'язання задач оптимізації на ЕОМ. - Дніпропетровськ: ДІБІ, 1992. - 63 с. 13. Ершова Н.М. Реализация в среде электронных таблиц математических методов и моделей управления производством. Методические указания и задания. – Днепропетровск: ПГАСА, 2001. – 42 с. 14. Методические указания к типовому расчету по разделу «Элементы линейной алгебры» курса «Высшая математика»/ Бараненко В.А., Ершова Н.М. и др. – Днепропетровск: ДИСИ, 1983. – 32 с. 15. Методические указания к лабораторным работам № 2, 3, 4 по темам: «Численные методы линейной алгебры и аппроксимация таблично заданных функций»/ Ершова Н.М., Семенец С.Н. – Днепропетровск: ДИСИ, 1986. – 44 с. 16. Методические указания к лабораторным работам № 5 и № 6 по теме «Решение задачи Коши для дифференциальных уравнений численными методами»/ Ершова Н.М. – Днепропетровск: ДИСИ, 1986. – 29 с. Приложение 1 Министерство образования и науки УКРАИНЫ Приднепровская государственная академия Строительства и архитектуры
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 224; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.180.245 (0.01 с.) |




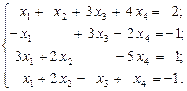
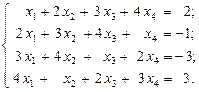

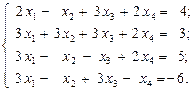


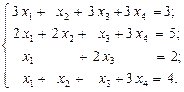
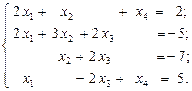
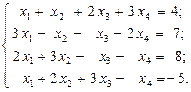
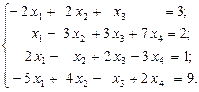
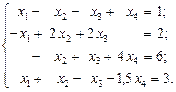



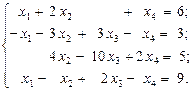



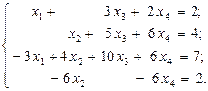





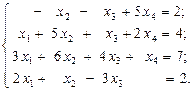







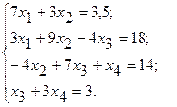 2.
2. 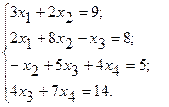
 4.
4. 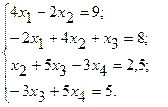
 6.
6. 
 8.
8. 
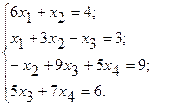 10.
10. 
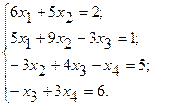 12.
12. 
 14.
14. 
 16.
16. 
 18.
18. 
 20.
20. 
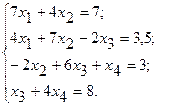 22.
22. 
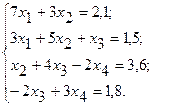 24.
24. 
 26.
26. 
 28.
28. 
 30.
30. 


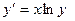
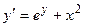















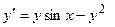





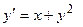


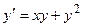

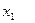








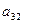




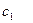
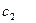
 - количество деталей каждого вида;
- количество деталей каждого вида;  - время, затрачиваемое
- время, затрачиваемое  - м типом станка на обработку одной детали
- м типом станка на обработку одной детали 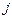 - го вида;
- го вида; 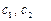 - прибыль от реализации одной детали
- прибыль от реализации одной детали  -го вида (
-го вида (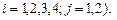



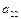




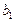



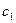

 с заданными объемами производства некоторой однородной продукции
с заданными объемами производства некоторой однородной продукции  и четыре пункта потребления
и четыре пункта потребления  с заданными объемами потребления
с заданными объемами потребления  этой продукции. Известны
этой продукции. Известны  - затраты на транспортировку единицы продукции из
- затраты на транспортировку единицы продукции из  -го пункта производства в
-го пункта производства в 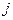 - й пункт потребления (
- й пункт потребления ( ). Требуется составить такой план перевозок
). Требуется составить такой план перевозок  , чтобы суммарные затраты на транспортировку были минимальными и были удовлетворены потребности во всех пунктах потребления.
, чтобы суммарные затраты на транспортировку были минимальными и были удовлетворены потребности во всех пунктах потребления.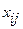 - количество единиц продукции, перевозимой из
- количество единиц продукции, перевозимой из