
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 4. Решение лоду и лнду второго порядка С постоянными коэффициентамиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оглавление
§ 9. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами Определение ЛОДУ второго порядка с постоянными коэффициентами Характеристическое уравнение: Случай1. Дискриминант больше нуля Случай2. Дискриминант равен нулю Случай3. Дискриминант меньше нуля Алгоритм нахождения общего решения ЛОДУ второго порядка с постоянными коэффициентами § 10. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами Определение ЛНДУ второго порядка с постоянными коэффициентами Метод вариации постоянных Метод решения ЛНДУ со специальной правой частью Теорема о структуре общего решения ЛНДУ 1. Функция r (x) – многочлен степени т 2. Функция r (x) – произведение числа на показательную функцию 3. Функция r (x) – сумма тригонометрических функций Алгоритм нахождения общего решения ЛНДУ со специальной правой частью Приложение § 9. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Дифференциальное уравнение второго порядка называется линейным однородным дифференциальным уравнением (ЛОДУ) с постоянными коэффициентами, если оно имеет вид:
где p и q – некоторые действительные числа. Для нахождения общего решения ЛОДУ достаточно найти два его различных частных решения
где С 1 и С 2 – произвольные независимые постоянные. Леонард Эйлер предложил искать частные решения ЛОДУ в виде
где k – некоторое число. Дифференцируя эту функцию два раза и подставляя выражения для у, у' и у" в уравнение
Полученное уравнение называется характеристическим уравнением ЛОДУ. Для его составления достаточно в исходном уравнении заменить у", у' и у соответственно на k 2, k и 1: Решив характеристическое уравнение, т.е. найдя корни k 1 и k 2,мы найдем и частные решения исходного ЛОДУ. Характеристическое уравнение
При этом возможны следующие три случая[2].
Случай 1. Дискриминант больше нуля, следовательно, корни k 1 и k 2 действительные и различные:
В этом случае общее решение ЛОДУ имеет вид:
где С 1 и С 2 – произвольные независимые постоянные.
Случай 2. Дискриминант равен нулю, следовательно, корни k 1 и k 2 действительные и равные:
В этом случае общее решение ЛОДУ имеет вид
где С 1 и С 2 – произвольные независимые постоянные.
Случай 3. Дискриминант меньше нуля. В этом случае уравнение не имеет действительных корней:
В этом случае общее решение ЛОДУ имеет вид
где С 1 и С 2 – произвольные независимые постоянные,
Таким образом, нахождение общего решения ЛОДУ второго порядка с постоянными коэффициентами сводится к нахождению корней характеристического уравнения и использованию формул общего решения уравнения (не прибегая к вычислению интегралов).
Алгоритм нахождения общего решения ЛОДУ второго порядка с постоянными коэффициентами: 1. Привести уравнение к виду 2. Составить характеристическое уравнение 3. Найти дискриминант характеристического уравнения. 4. Используя формулы (см. Таблицу 1), в зависимости от знака дискриминанта записать общее решение. Таблица 1 Таблица возможных общих решений
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 2631; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.193.70 (0.011 с.) |

 ,
, и
и  . Тогда общее решение ЛОДУ будет иметь вид
. Тогда общее решение ЛОДУ будет иметь вид ,
, ,
, ,
, 



 .
. k 1 ¹ k 2
k 1 ¹ k 2 ,
, k 1 = k 2 = k
k 1 = k 2 = k ,
,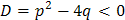 , корней нет.
, корней нет. ,
, ,
,  .
.


